
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение расчетного контактного напряжения
|
|
|
|
Проверочный расчет на контактную выносливость активных поверхностей зубьев
Нормы точности зубчатых колес
| Степень точности по ГОСТ 1643-81 | Окружная скорость, м/с | |
| Прямые зубья | Непрямые зубья | |
| 5 и выше | > 15 | > 30 |
 15 15
|  30 30
| |
 10 10
|  15 15
| |
 6 6
|  10 10
| |
 2 2
|  4 4
|
Контактная выносливость устанавливается сопоставлением действующим в полосе зацепления расчетного и допускаемого контактного напряжений:
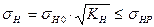 , (4.1)
, (4.1)
где KH – коэффициент нагрузки; 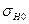 – контактное напряжение в полюсе зацепления при KH = 1.
– контактное напряжение в полюсе зацепления при KH = 1.
Контактное напряжение в полюсе зацепления при KH = 1 определяют следующим образом, МПа:
 (4.2)
(4.2)
где «+» для наружного зацепления, «–» для внутреннего зацепления;
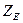 – коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес;
– коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес;
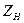 – коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления;
– коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления;
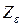 – коэффициент, учитывающий суммарную длину контактных линий;
– коэффициент, учитывающий суммарную длину контактных линий;
FtH – окружная сила на делительном цилиндре, Н;
 – рабочая ширина венца зубчатой передачи, мм;
– рабочая ширина венца зубчатой передачи, мм;
d 1 – делительный диаметр шестерни, мм.
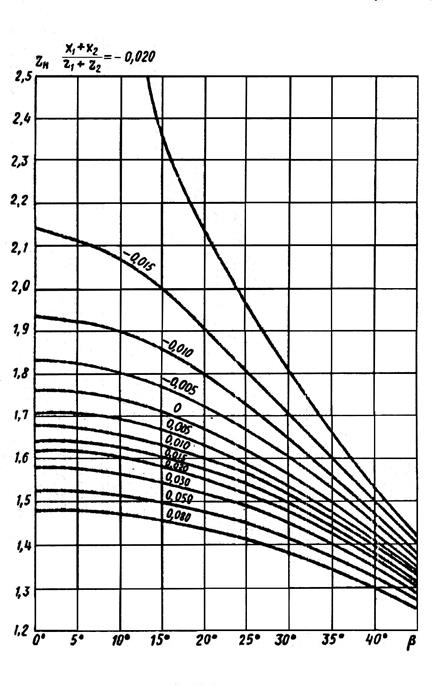
Коэффициент 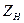 , учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления, определяется по кривым (рис. 4.1.) в зависимости от угла наклона зубьев и отношения суммы коэффициентов смещений к сумме чисел зубьев
, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления, определяется по кривым (рис. 4.1.) в зависимости от угла наклона зубьев и отношения суммы коэффициентов смещений к сумме чисел зубьев 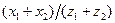 , а так же может быть определен по таблице 4.1. либо по формуле:
, а так же может быть определен по таблице 4.1. либо по формуле:
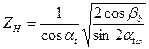 , (4.3)
, (4.3)
где 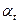 – делительный угол профиля в торцевом сечении:
– делительный угол профиля в торцевом сечении:  ,
,
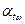 – угол зацепления:
– угол зацепления: 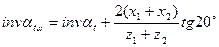 ;
;
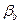 – основной угол наклона:
– основной угол наклона: 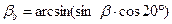 .
.
Таблица 4.1
Значения коэффициент 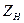
Угол наклона
линии зуба 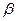 , град , град
| Значения 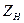 при относительном смещении контура при относительном смещении контура 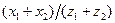
| |||||||||||||
| 0,080 | 0,050 | 0,030 | 0,020 | 0,010 | 0,005 | -0,005 | -0,010 | -0,015 | -0,020 | |||||
| 1,48 | 1,52 | 1,58 | 1,62 | 1,68 | 1,71 | 1,76 | 1,83 | 1,93 | 2,14 | - | ||||
| 1,47 | 1,51 | 1,56 | 1,60 | 1,66 | 1,69 | 1,74 | 1,80 | 1,90 | 2,07 | - | ||||
| 1,46 | 1,50 | 1,55 | 1,58 | 1,63 | 1,67 | 1,71 | 1,77 | 1,86 | 2,00 | 2,35 | ||||
| 1,43 | 1,47 | 1,52 | 1,55 | 1,60 | 1,63 | 1,67 | 1,72 | 1,80 | 1,91 | 2,13 | ||||
| 1,42 | 1,45 | 1,49 | 1,52 | 1,57 | 1,59 | 1,62 | 1,67 | 1,73 | 1,81 | 1,97 | ||||
| 1,38 | 1,42 | 1,45 | 1,48 | 1,52 | 1,54 | 1,56 | 1,60 | 1,65 | 1,70 | 1,81 | ||||
| 1,35 | 1,37 | 1,40 | 1,42 | 1,46 | 1,48 | 1,50 | 1,53 | 1,56 | 1,60 | 1,66 | ||||
| 1,30 | 1,32 | 1,34 | 1,37 | 1,39 | 1,41 | 1,42 | 1,45 | 1,47 | 1,50 | 1,53 | ||||
Коэффициент 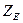 , учитывающий механические свойства материалов сопряженных зубчатых колес определяется по формуле:
, учитывающий механические свойства материалов сопряженных зубчатых колес определяется по формуле:
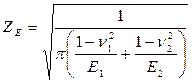 , (4.4)
, (4.4)
где ν – коэффициент Пуассона, E – модуль упругости материалов, МПа.
Для E 1 =E 2 =Е и  принимают
принимают 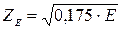 .
.
Для стали при  МПа
МПа 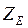 = 190.
= 190.
|
Рис. 4.1. График для нахождения коэффициента 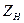
|
Коэффициент 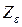 , учитывающий суммарную длину контактных линий, определяется по формулам:
, учитывающий суммарную длину контактных линий, определяется по формулам:
 , при
, при  ;
;
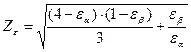 , при
, при  ; (4.5)
; (4.5)
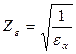 , при
, при  ,
,
где 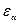 – коэффициент торцевого перекрытия, в общем случае определяется по формуле:
– коэффициент торцевого перекрытия, в общем случае определяется по формуле:
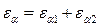 ,
,
где составляющие коэффициента торцевого перекрытия:
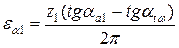 ,
, 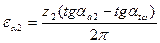 ,
,
где  ,
,
Для передач без смещений при 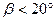 :
:  ;
;
 – коэффициент осевого перекрытия, определяется по формуле:
– коэффициент осевого перекрытия, определяется по формуле:
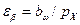 ,
,
где  – осевой шаг:
– осевой шаг: 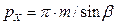 . Тогда:
. Тогда: 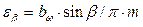 .
.
Коэффициент 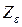 так же можно определить по кривой, представленной на рис. 4.2.
так же можно определить по кривой, представленной на рис. 4.2.

| ||||
Рис. 4.2. График для нахождения коэффициента 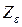
|
Окружная сила на делительном цилиндре 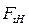 определяется по формуле:
определяется по формуле:
 , (4.6)
, (4.6)
где 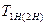 – вращающий момент на шестерне (колесе), Нм;
– вращающий момент на шестерне (колесе), Нм;  – делительный диаметр шестерни (колеса), мм.
– делительный диаметр шестерни (колеса), мм.
Коэффициент нагрузки  определяют по зависимости:
определяют по зависимости:
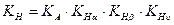 , (4.7)
, (4.7)
где 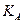 – коэффициент, учитывающий внешнюю динамическую нагрузку;
– коэффициент, учитывающий внешнюю динамическую нагрузку;
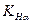 – коэффициент, учитывающий неравномерность распределение нагрузки между зубьями;
– коэффициент, учитывающий неравномерность распределение нагрузки между зубьями;
 – коэффициент, учитывающий неравномерность распределения нагрузки по ширине зуба;
– коэффициент, учитывающий неравномерность распределения нагрузки по ширине зуба;
 – коэффициент, учитывающий динамическую нагрузку.
– коэффициент, учитывающий динамическую нагрузку.
Коэффициент, учитывающий внешнюю динамическую нагрузку, 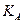 = 1, если в циклограмме учтены внешние динамические нагрузки, в противном случае при расчетах зубьев на усталостную прочность можно воспользоваться ориентировочными данными, приведенными в табл. 4.2 с учетом табл. 4.3 и 4.4.
= 1, если в циклограмме учтены внешние динамические нагрузки, в противном случае при расчетах зубьев на усталостную прочность можно воспользоваться ориентировочными данными, приведенными в табл. 4.2 с учетом табл. 4.3 и 4.4.
Таблица 4.2
Коэффициент внешней динамической нагрузки
при расчетах на усталостную прочность 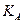
| Режим нагружения двигателя | Режим нагружения ведомой машины | |||
| равномерное | с малой неравномерностью | со средней неравномерностью | со значительной неравномерностью | |
| Равномерный | 1,00 | 1,25 | 1,50 | 1,75 |
| С малой неравномерностью | 1,10 | 1,35 | 1,60 | 1,85 |
| Со средней неравно мерностью | 1,25 | 1,50 | 1,75 | 2,00 и выше |
| Со значительной неравномерностью | 1,50 | 1,75 | 2,00 | 2,25 и выше |
Примечания:
1. Табличные значения равны отношению эквивалентных нагрузок к номинальным и распространяются на передачи, работающие вне резонансной области.
2. При наличии в приводе гидравлических и упругих муфт, демпфирующих колебания, табличные значения коэффициентов КА могут быть уменьшены на 20—30 % при условии, что 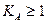 .
.
Таблица 4.3
Характерные режимы нагружения двигателей
| Режим нагружения | Вид двигателя |
| Равномерный | Электродвигатель; паровые и газовые турбины при стабильных режимах эксплуатации и небольших пусковых моментах |
| С малой неравномерностью | Гидравлические двигатели, паровые и газовые турбины при больших часто возникающих пусковых моментах |
| Со средней неравномерностью | Многоцилиндровый двигатель внутреннего сгорания |
| Со значительной неравномерностью | Одноцилиндровый двигатель внутреннего сгорания |
Таблица 4.4
Характерные режимы нагружения ведомых машин
| Режим нагружения | Вид рабочей машины |
| Равномерный | Электрический генератор; равномерно работающие ленточные, пластинчатые конвейеры; легкие подъемники; упаковочные машины; вентиляторы; перемешивающие устройства и мешалки для веществ равномерной плотности; турбокомпрессоры; легкие центрифуги; механизмы с вращающимися деталями |
| С малой неравномерностью | Неравномерно работающие ленточные и пластинчатые транспортеры (для штучных грузов); шестеренчатые и ротационные насосы; главные приводы станков; тяжелые подъемники; механизмы с вращающимися деталями кранов; промышленные и рудничные вентиляторы; тяжелые центрифуги; перемешивающие устройства и мешалки для веществ с переменной плотностью; поршневые многоцилиндровые, струйные и дозировочные насосы; экструдеры; каландры, вращающиеся печи; станы холодной прокатки |
| Со средней неравномерностью | Экструдеры для резины; мешалки с прерывающимся процессом для резины и пластмасс; легкие шаровые мельницы; деревообрабатывающие станки (пилы, токарные); одноцилиндровые поршневые насосы; нереверсивные станы горячей прокатки; подъемные машины |
| Со значительной неравномерностью | Экскаваторы, черпалки (приводы ковшей, цепных черпалок, грохотов); тяжелые шаровые мельницы; резиносмесители; дробилки (для камня и руды); кузнечные машины; тяжелые дозировочные насосы; ротационные буровые машины; брикетные прессы; реверсивные станы горячей прокатки |
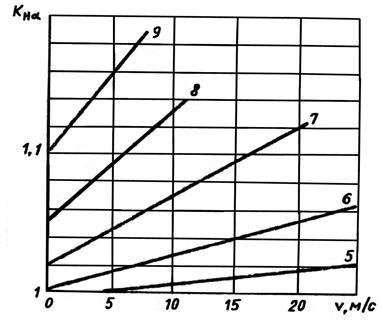
Коэффициент 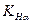 , учитывающий неравномерность распределения нагрузки между зубьями. Данный коэффициент для косозубых и шевронных передач определяется по таблице 4.5 или по кривой (рис. 4.3) в зависимости от окружной скорости и степени точности по нормам плавности. Для прямозубых передач
, учитывающий неравномерность распределения нагрузки между зубьями. Данный коэффициент для косозубых и шевронных передач определяется по таблице 4.5 или по кривой (рис. 4.3) в зависимости от окружной скорости и степени точности по нормам плавности. Для прямозубых передач  . Более точно коэффициент
. Более точно коэффициент 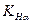 может быть посчитан по ГОСТ 21354-87.
может быть посчитан по ГОСТ 21354-87.
Таблица 4.5
Значения коэффициент 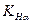
| Окружная скорость v, м/с | Значения коэффициента 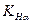 при степени точности по нормам плавности работы
(ГОСТ 1643-72) при степени точности по нормам плавности работы
(ГОСТ 1643-72)
| ||||
| 2,5 | 1,01 | 1,03 | 1,05 | 1,13 | |
| 1,02 | 1,05 | 1,09 | 1,16 | ||
| 1,01 | 1,03 | 1,07 | 1,13 | - | |
| 1,01 | 1,04 | 1,09 | - | - | |
| 1,02 | 1,05 | 1,12 | - | - | |
| 1,02 | 1,06 | - | - | - |
|
Рис. 4.3. График для нахождения коэффициента 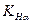
|
Коэффициент 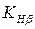 , учитывающий неравномерность распределения нагрузки по длине контактных линий, принимают в зависимости от параметра
, учитывающий неравномерность распределения нагрузки по длине контактных линий, принимают в зависимости от параметра  , схемы передачи и твердости активных поверхностей зубьев по графику, представленному на рис. 3.1. Более точно коэффициент
, схемы передачи и твердости активных поверхностей зубьев по графику, представленному на рис. 3.1. Более точно коэффициент 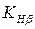 может быть посчитан по ГОСТ 21354-87.
может быть посчитан по ГОСТ 21354-87.
Коэффициент  , учитывающий динамическую нагрузку можно определить по таблице 5.1, в зависимости от степени точности, окружной скорости, твердости зубьев и характеристики передачи, либо по формуле:
, учитывающий динамическую нагрузку можно определить по таблице 5.1, в зависимости от степени точности, окружной скорости, твердости зубьев и характеристики передачи, либо по формуле:
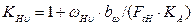 , (4.8)
, (4.8)
где 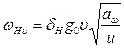 ,
,
где  – удельная окружная динамическая сила, Н/мм;
– удельная окружная динамическая сила, Н/мм;  – окружная скорость на делительном цилиндре, м/с.
– окружная скорость на делительном цилиндре, м/с.
Коэффициент 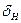 , учитывающий влияние вида зубчатой передачи, модификации профиля головок зубьев и определяется по таблице 4.6.
, учитывающий влияние вида зубчатой передачи, модификации профиля головок зубьев и определяется по таблице 4.6.
Коэффициент g 0, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса, определяется по таблице 4.7.
Таблица 4.6
Значения коэффициента 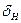
| Твердость поверхностей зубьев по Виккерсу | Вид зубьев | 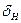
|
Н1  НV 350 или
Н2 НV 350 или
Н2  НV 350 НV 350
| Прямые, без модификации головок Прямые, с модификацией головок Косые | 0,06 0,04 0,02 |
| Н1 >НV 350 и Н2 > НV 350 | Прямые, без модификации головок Прямые, с модификацией головок Косые | 0,14 0,10 0,04 |
Таблица 4.7
Значения коэффициента 
| Модуль m, мм | 
| |||||
| Степень точности по нормам плавности по ГОСТ 1643-81 | ||||||
 3,55
3,55…10
>10 3,55
3,55…10
>10
| 2,8 3,1 3,7 | 3,8 4,2 4,8 | 4,7 5,3 6,4 | 5,6 6,1 7,3 | 7,3 8,2 10,0 | 10,0 11,0 13,5 |
Полученные значение  не должно превышать предельного значения
не должно превышать предельного значения 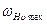 , приведенного в таблице 4.8. В противном случае следует принимать
, приведенного в таблице 4.8. В противном случае следует принимать 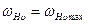 .
.
Таблица 4.8
Предельные значения 
| Модуль m, мм | Степень точности по нормам плавности по ГОСТ 1643-81 | |||||
 3,55
3,55…10
>10 3,55
3,55…10
>10
|
|
|
|
|
|
Дата добавления: 2015-07-13; Просмотров: 350; Нарушение авторских прав?; Мы поможем в написании вашей работы!
