
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теоретические упражнения 1 страница
|
|
|
|
Теоретические вопросы
IV. ИНТЕГРАЛЫ
1. Понятие первообразной функции. Теоремы о первообразных.
2. Неопределенный интеграл, его свойства.
3. Таблица неопределенных интегралов.
4. Замена переменной и интегрирование по частям в неопределенном интеграле.
5. Разложение дробной рациональной функции на простейшие дроби.
6. Интегрирование простейших дробей. Интегрирование рациональных функций.
7 Интегрирование выражений, содержащих тригонометрические функции.
8. Интегрирование иррациональных выражений.
9. Понятие определенного интеграла, его геометрический смысл.
10. Основные свойства определенного интеграла.
11. Теорема о среднем.
12. Производная определенного интеграла по верхнему пределу. Формула Ньютона – Лейбница.
13. Замена переменной и интегрирование по частям в определенном интеграле.
14. Интегрирование биномиальных дифференциалов.
15. Вычисление площадей плоских фигур.
16. Определение и вычисление длины кривой, дифференциал длины дуги кривой.
1. Считая, что функция 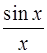 равна 1 при
равна 1 при 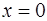 , доказать, что она интегрируема на отрезке
, доказать, что она интегрируема на отрезке 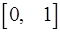 .
.
2. Какой из. интегралов больше:
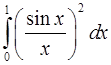 или
или  ?
?
3. Пусть 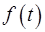 – непрерывная функция, а функции
– непрерывная функция, а функции 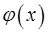 и
и 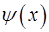 дифференцируемые. Доказать, что
дифференцируемые. Доказать, что
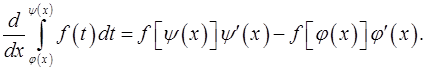
4. Найти 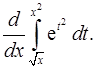
5. Найти точки экстремума функции

6. Пусть 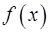 – непрерывная периодическая функция с периодом
– непрерывная периодическая функция с периодом 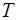 . Доказать, что
. Доказать, что
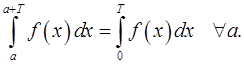
7. Доказать, что если 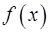 – четная функция, то
– четная функция, то
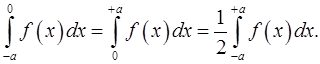
8. Доказать, что для нечетной функции 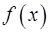 справедливы равенства
справедливы равенства
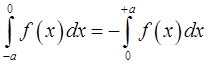 и
и 
Чему равен интеграл 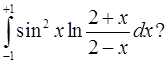
9. При каком условии, связывающем коэффициенты 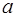 ,
, 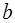 ,
, 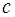 интеграл
интеграл 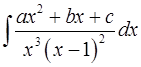 является рациональной функцией?
является рациональной функцией?
10. При каких целых значениях 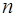 интеграл
интеграл 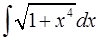 выражается элементарными функциями.
выражается элементарными функциями.
Расчетные задания
Задача 1. Вычислить неопределенные интегралы.
1.1. 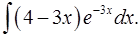 1.2.
1.2. 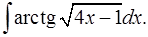
1.3. 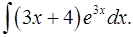 1.4.
1.4. 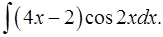
1.5. 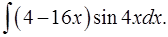 1.6.
1.6. 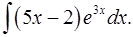
1.7. 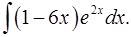 1.8.
1.8. 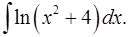
1.9. 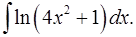 1.10.
1.10. 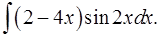
1.11.  1.12.
1.12. 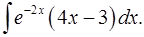
1.13.  1.14.
1.14. 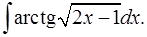
1.15.  1.16.
1.16. 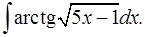
1.17. 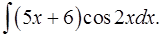 1.18.
1.18. 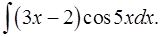
1.19. 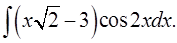 1.20.
1.20. 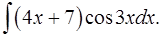
1.21. 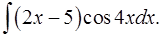 1.22.
1.22. 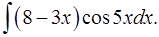
1.23. 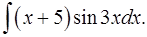 1.24.
1.24. 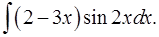
1.25. 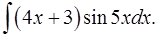 1.26.
1.26. 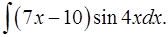
1.27. 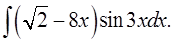 1.28.
1.28. 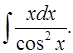
1.29. 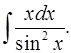 1.30.
1.30. 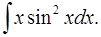
1.31. 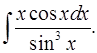
Задача 2. Вычислить определенные интегралы.
2.1. 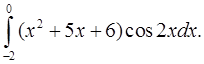 2.2.
2.2. 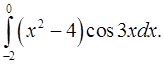
2.3. 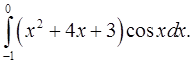 2.4.
2.4. 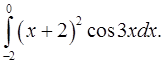
2.5. 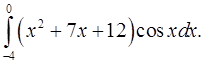 2.6.
2.6. 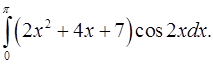
2.7. 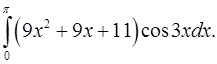 2.8.
2.8. 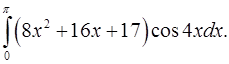
2.9. 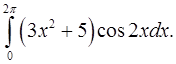 2.10.
2.10. 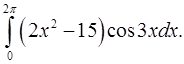
2.11. 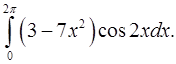 2.12.
2.12. 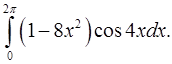
2.13. 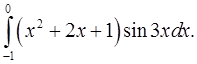 2.14.
2.14. 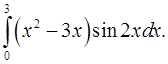
2.15. 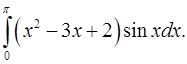 2.16.
2.16. 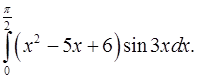
2.17. 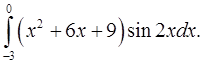 2.18.
2.18. 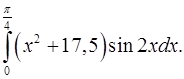
2.19. 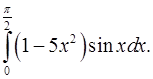 2.20.
2.20. 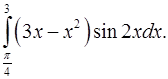
2.21. 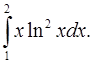 2.22.
2.22. 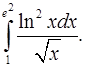
2.23. 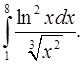 2.24.
2.24. 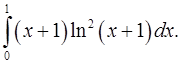
2.25. 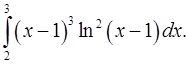 2.26.
2.26. 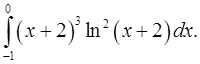
2.27. 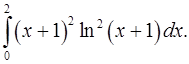 2.28.
2.28. 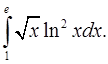
2.29. 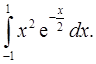 2.30.
2.30. 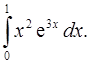
2.31. 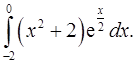
Задача 3. Найти неопределенные интегралы.
3.1. 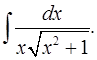 3.2.
3.2. 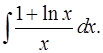
3.3. 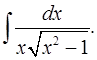 3.4.
3.4. 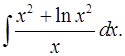
3.5. 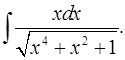 3.6.
3.6. 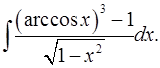
3.7. 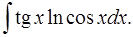 3.8.
3.8. 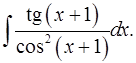
3.9. 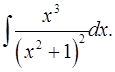 3.10.
3.10. 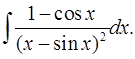
3.11. 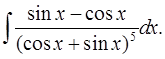 3.12.
3.12. 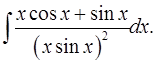
3.13. 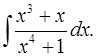 3.14.
3.14. 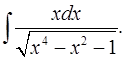
3.15. 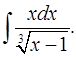 3.16.
3.16. 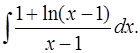
3.17.  3.18.
3.18. 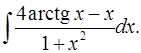
3.19. 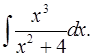 3.20.
3.20. 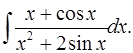
3.21. 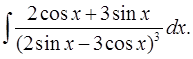 3.22.
3.22. 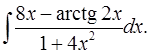
3.23. 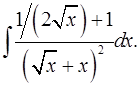 3.24.
3.24. 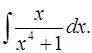
3.25. 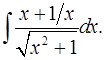 3.26.
3.26. 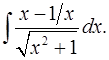
3.27. 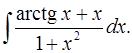 3.28.
3.28. 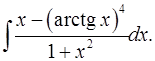
3.29. 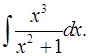 3.30.
3.30. 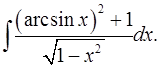
3.31. 
Задача 4. Вычислить определенные интегралы.
4.1. 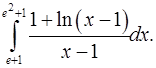 4.2.
4.2. 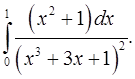
4.3. 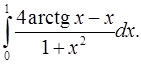 4.4.
4.4. 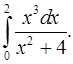
4.5. 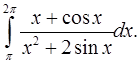 4.6.
4.6. 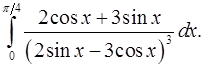
4.7. 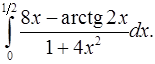 4.8.
4.8. 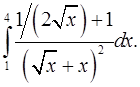
4.9. 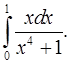 4.10.
4.10. 
4.11. 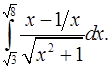 4.12.
4.12. 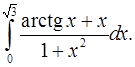
4.13. 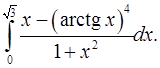 4.14.
4.14. 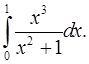
4.15. 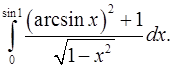 4.16.
4.16. 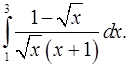
4.17. 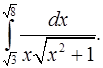 4.18.
4.18. 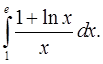
4.19. 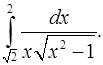 4.20.
4.20. 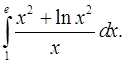
4.21. 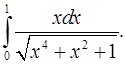 4.22.
4.22. 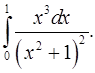
4.23. 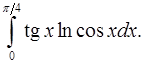 4.24.
4.24. 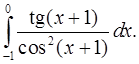
4.25. 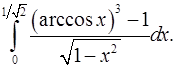 4.26.
4.26. 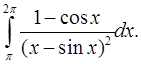
4.27. 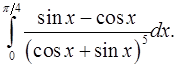 4.28.
4.28. 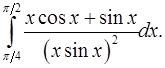
4.29. 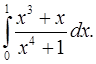 4.30.
4.30. 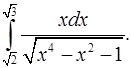
4.31. 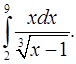
Задача 5. Найти неопределенные интегралы.
5.1. 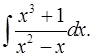 5.2.
5.2. 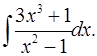
5.3. 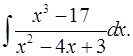 5.4.
5.4. 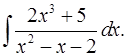
5.5. 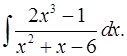 5.6.
5.6. 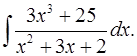
5.7. 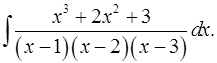 5.8.
5.8. 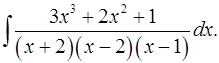
5.9. 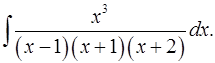 5.10.
5.10. 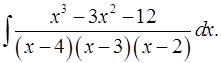
5.11. 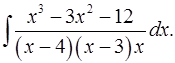 5.12.
5.12. 
5.13. 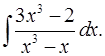 5.14.
5.14. 
5.15. 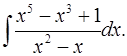 5.16.
5.16. 
5.17. 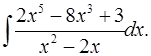 5.18.
5.18. 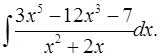
5.19. 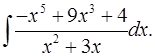 5.20.
5.20. 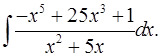
5.21. 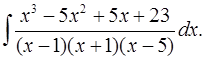 5.22.
5.22. 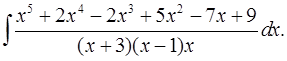
5.23. 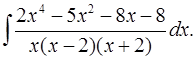 5.24.
5.24. 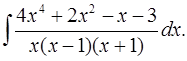
5.25. 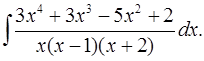 5.26.
5.26. 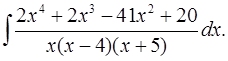
5.27. 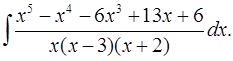 5.28.
5.28. 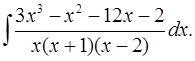
5.29. 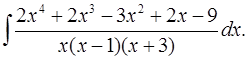 5.30.
5.30. 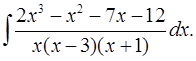
5.31. 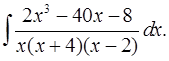
Задача 6. Найти неопределенные интегралы.
6.1. 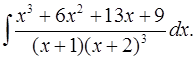 6.2.
6.2. 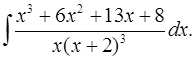
6.3. 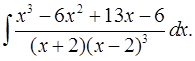 6.4.
6.4. 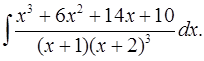
6.5. 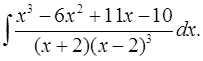 6.6.
6.6. 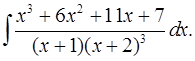
6.7. 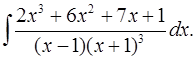 6.8.
6.8. 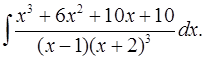
6.9.  6.10.
6.10. 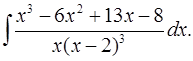
6.11. 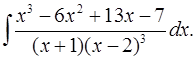 6.12.
6.12. 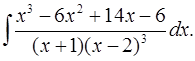
6.13.  6.14.
6.14. 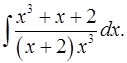
6.15.  6.16.
6.16. 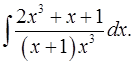
6.17. 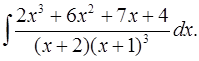 6.18.
6.18. 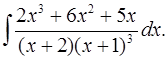
6.19. 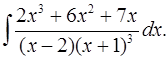 6.20.
6.20. 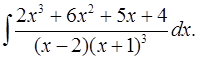
6.21. 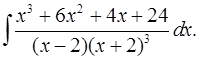 6.22.
6.22. 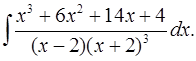
6.23. 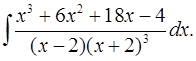 6.24.
6.24. 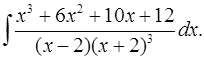
6.25. 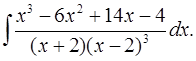 6.26.
6.26. 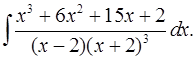
6.27. 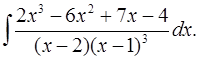 6.28.
6.28. 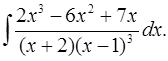
6.29. 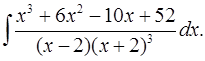 6.30.
6.30. 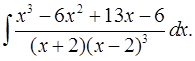
6.31. 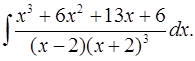
Задача 7. Найти неопределенные интегралы.
7.1. 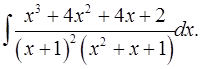 7.2.
7.2. 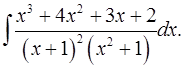
7.3. 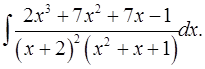 7.4.
7.4. 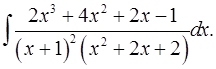
7.5. 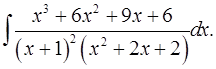 7.6.
7.6. 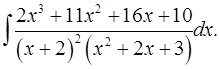
7.7. 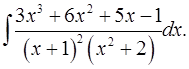 7.8.
7.8. 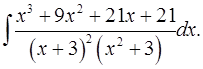
7.9. 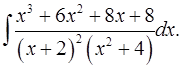 7.10.
7.10. 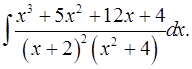
7.11. 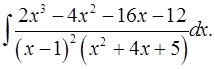 7.12.
7.12. 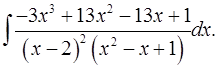
7.13. 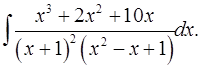 7.14.
7.14. 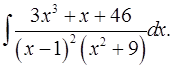
7.15. 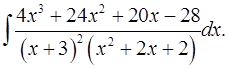 7.16.
7.16. 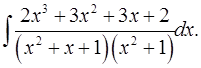
7.17. 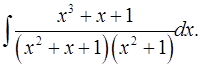 7.18.
7.18. 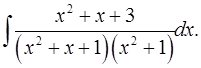
7.19. 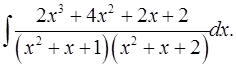 7.20.
7.20. 
7.21. 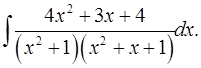 7.22.
7.22. 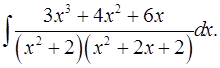
7.23. 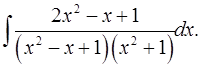 7.24.
7.24. 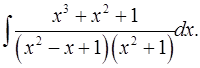
7.25. 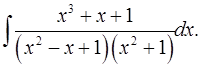 7.26.
7.26. 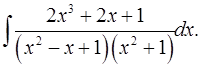
7.28. 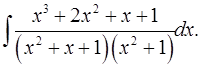 7.29.
7.29. 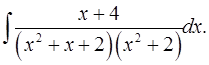
7.30. 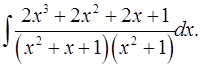 7.30.
7.30. 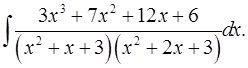
7.31. 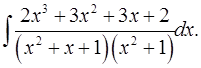
Задача 8. Вычислить определенные интегралы.
8.1. 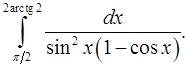 8.2.
8.2. 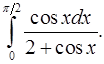
8.3. 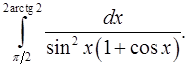 8.4.
8.4. 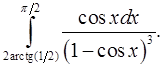
8.5. 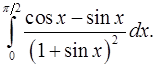 8.6.
8.6. 
8.7. 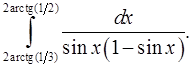 8.8.
8.8. 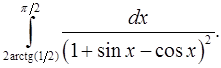
8.9.  8.10.
8.10. 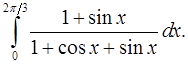
8.11. 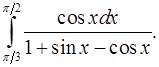 8.12.
8.12. 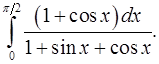
8.13. 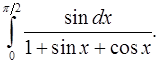 8.14.
8.14. 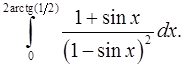
8.15. 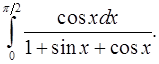 8.16.
8.16. 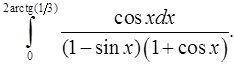
8.17. 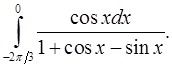 8.18.
8.18. 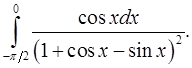
8.19. 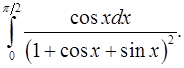 8.20.
8.20. 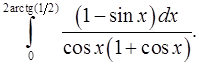
8.21. 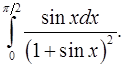 8.22.
8.22. 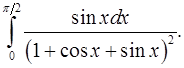
8.23. 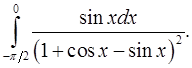 8.24.
8.24. 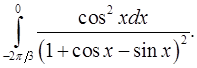
8.25. 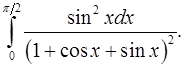 8.26.
8.26. 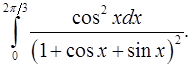
8.27. 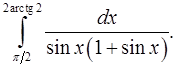 8.28.
8.28. 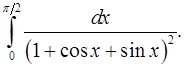
8.29. 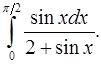 8.30.
8.30. 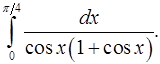
8.31. 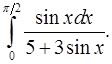
Задача 9. Вычислить определенные интегралы.
9.1. 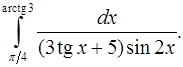 9.2.
9.2. 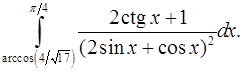
9.3. 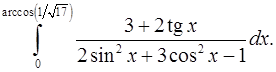 9.4.
9.4. 
9.5. 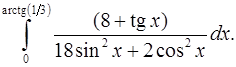 9.6.
9.6. 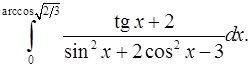
9.7. 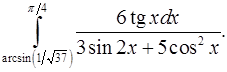 9.8.
9.8. 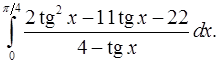
9.9. 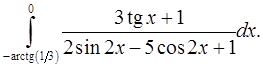 9.10.
9.10. 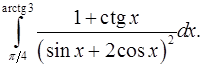
9.11. 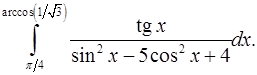 9.12.
9.12. 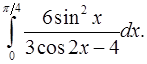
9.13.  9.14.
9.14. 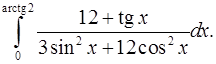
9.15. 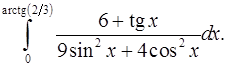 9.16.
9.16. 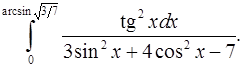
9.17. 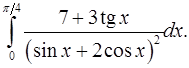 9.18.
9.18. 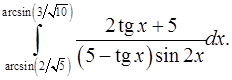
9.19. 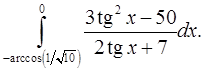 9.20.
9.20. 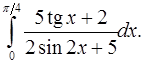
9.21. 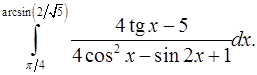 9.22.
9.22. 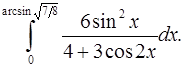
9.23.  9.24.
9.24. 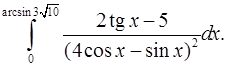
9.25. 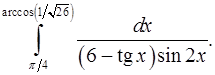 9.26.
9.26. 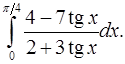
9.27. 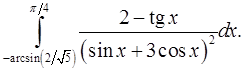 9.28.
9.28. 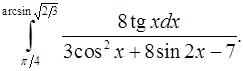
9.29. 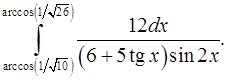 9.30.
9.30. 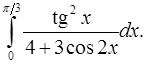
9.31. 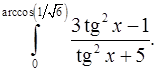
Задача 10. Вычислить определенные интегралы.
10.1. 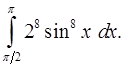 10.2.
10.2. 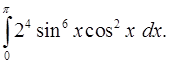
|
|
|
|
|
Дата добавления: 2015-07-13; Просмотров: 241; Нарушение авторских прав?; Мы поможем в написании вашей работы!