Основные элементы систем нефтегазосбора. 2 страница

2. по функции - выкидные линии и коллекторы. Выкидные линии-трубопроводы от устья скважины до ГЗУ. Коллекторы-трубопроводы, собирающие продукцию скважин от групповых установок к сборным пунктам.

3. по величине рабочего давления – низкого (до 1,6МПа), среднего (от 1,6 до 2,5 МПа) и высокого (выше 2,5МПа).

Трубопроводы среднего и высокого давления – напорные. Трубопроводы низкого давления могут быть напорными и самотечными.

Если в самотечных трубопроводах движение жидкости происходит при полном заполнении ею объема трубы, то движение напорно-самотечное, если заполнение не полное, то движение характеризуется как свободно-самотечное.

4. по гидравлической схеме работы - простые и сложные.

Простые - трубопроводы, имеющие неизменный диаметр и массовый расход транспортируемой среды по всей длине.

Сложные - трубопроводы, имеющие различные ответвления или изменяющийся по длине диаметр. Сложные трубопроводы можно разбить на участки, каждый из которых является простым трубопроводом.

5. По способам прокладки:

-подземные,

- наземные,

- подводные,

-подвесные.

Сложный трубопровод может иметь различные диаметры по длине и отводы.

При гидравлическом расчете их практический интерес пред­ставляет четыре случая, часто встречающихся в промысловых условиях:

1) жидкость из раздаточного коллектора, имеющего постоян­ный диаметр, равномерно или неравномерно отбирается;

2) жидкость равномерно или неравномерно поступает в сбор­ный коллектор, имеющий по длине разный диаметр;

3) общий сборный коллектор образует параллельные трубо­проводы (лупинги);

4) общий сборный (раздаточный) коллектор имеет форму кольца (магистральный водовод).

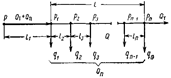
Рассмотрим решение задач для каждого случая при условии установившегося течения.

Уравнение материального баланса для первого случая (см. рис.1) - раздаточного коллектора

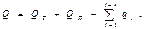
где Q - объемный расход жидкости в произвольном сечении; Q _T - транзитный расход жидкости, т. е. расход, который транс­портируется за пределы указанных участков; Q _П - путевой расход жидкости; q ₁, q ₂, …., q_i - равные или неравные объемные расходы жидкости в ответвлениях, отстоящих на расстоянии l ₁, l ₂, …., l_i от начала трубопровода.

Расход жидкости на участках:

l₁ = О _T + Q _П;

l₂ = О _T + Q _П - q ₁;

l₃ = О _T + Q _П - (q ₁ + q ₂);

l_n = О _T + Q _П - (q ₁ + q ₂ + ….. + q_{n - 1}).

Поскольку диаметр раздаточного коллектора одинаков на всем протяжении, а расходы жидкости на различных участках, в связи с ее отбором, разные, то режимы течения на каждом уча­стке l ₁, l ₂, …., l _П также будут разными.

Определим перепад давления на каждом участке горизонтального трубопровода по формуле Лейбензона 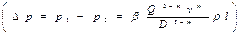. На первом участке

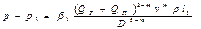
На втором участке

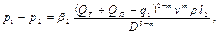
На третьем участке

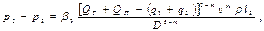
на n -м участке

Сложив перепады на каждом участке, найдем общий перепад на всей длине рассматриваемого раздаточного коллектора:

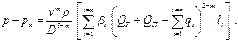
Если транзитный расход в раздаточном коллекторе равен нулю, т. е. Q _T = 0, величины отборов одинаковы (q ₁ = q ₂ = q ₃ = ….. q_n), расстояния между отборами равны между собой (l ₁ = l ₂ = …. L_n), то

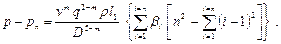
С учетом рельефа местности формула примет вид

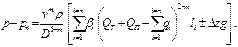
Для каждого участка трубопровода определяется режим дви­жения жидкости и по формуле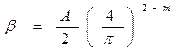

Уравнение материального баланса для второго случая - сборного коллектора

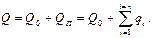
Расход жидкости на участках

l₁ = О ₀;

l₂ = О ₀ + q ₁;

l₃ = О ₀ + q ₁ + q ₂ и т. д.

Определим перепад давления на каждом участке по аналогии с предыдущим.

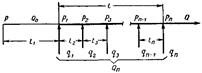
Рис. 2. Расчетная схема сложного нефтепровода, имеющего по длине разные диаме­тры, с сосредоточен­ным поступлением нефти

На первом участке

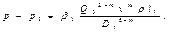
На втором участке

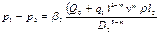
На третьем участке

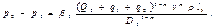
На n -м участке

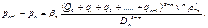
Как и в первом случае, сложив перепады давлений на каждом участке, найдем общий перепад на всей длине рассматриваемого сборного коллектора:

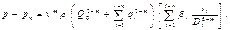
Для каждого участка сборного коллектора определяют режим движения жидкости и определяют перепад давления на каждом участке. Затем производится сложение этих перепадов, в результате чего получается общий перепад.Расчет параллельных и кольцевых трубопроводов.

Сложный трубопровод может иметь различные диаметры по длине и отводы.При гидравлическом расчете их практический интерес пред­ставляет четыре случая, часто встречающихся в промысловых условиях:

1) жидкость из раздаточного коллектора, имеющего постоянный диаметр, равномерно или неравномерно отбирается; 2) жидкость равномерно или неравномерно поступает в сборный коллектор, имеющий по длине разный диаметр; 3) общий сборный коллектор образует параллельные ТП (лупинги); 4) общий сборный (раздаточный) коллектор имеет форму кольца (магистральный водовод).

Параллельные ТП, или лупинги, прокладывают обычно для увеличения их пропускной способности при сохране­нии того же перепада давления на конечных участках или умень­шении его.

Рис. 3. Расчетная схема параллель­ных трубопроводов (с лупингом)

На рис. 3 приведена схема трубопровода с лупингом.

Из баланса количества жидкости имеем

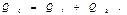где Q ₀ - расход жидкости в основном трубопроводе до сечения А и после сечения В; Q ₁ - расход жидкости в трубопроводе на участке АВ; Q ₂ - расход жидкости в лупинге.

Очевидно, потери напора на участке трубопровода АВ равны потери напора в лупинге (параллельной трубе), т. е. D h ₁ = D h ₂ или, можем записать:

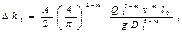
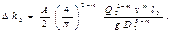
где l ₀ - длина участка трубопровода, равная длине лупинга; D ₁, D ₂ - диаметры трубопровода и лупинга соответственно.

Из равенства потерь напора на участке трубопровода А - В следует

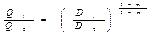
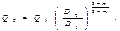
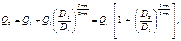
откуда найдем расход в трубопроводе Q ₁ на участке AВ, выра­женный через расход Q ₀ до разветвления:

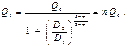
Формула (7) позволяет определить расход жидкости в сдво­енном трубопроводе по известному суммарному расходу Q ₀ и заданным отношениям диаметров лупинга и трубопровода.

Гидравлический уклон до участка АВ и после него

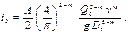
Гидравлический уклон на участке АВ и в лупинге одинаков и будет равен с учетом выражения (7)

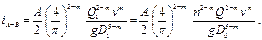
Выражая гидравлический уклон на сдвоенном участке через гидравлический уклон основного трубопровода, получим

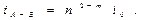
Если диаметр основного трубопровода D ₁ и диаметр лупинга D ₂ равны между собой, то

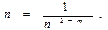
В этом случае при ламинарном режиме n = 0,5, при турбу­лентном режиме в зоне справедливой для формулы Блазиуса n = 0,297, для зоны с квадратичной характеристикой n = 0,25.

Кольцевые трубопроводы сравнительно широко применяют в промысловых условиях при подаче воды от мест водозабора до кустовых насосных станций (КНС).

Кольцевые трубопроводы рассчитывают по той же схеме, что и при параллельном соединении (с лупингом).

Однако задача значительно усложняется тем, что здесь имеется несколько расходных пунктов Q ₁, Q ₂, Q ₃, Q ₄, Q ₅ (рис. 4), и рас­чет проводят до тех пор, пока изменением расхода жидкости и направлением ее движения не будет достигнуто равенство потерь напора в ветвях ВСДЕ и ВМКЕ.

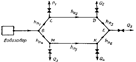
Рис. 4. Расчетная схема кольцевого трубопровода

При проектировании кольцевой системы водоводов вначале задаются величинами расходов Q ₁, Q ₂, Q ₃, Q ₄, Q ₅ и, зная диаметры отдельных ветвей, определяют значения потерь напора от общей точки разветвления В до расходных пунктов СDЕ и МКЕ. Рас­ходы считаются заданными правильно, если алгебраическая сумма потерь напора в кольце равна нулю, т. е.

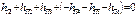или

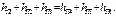
Если это условие не соблюдается, то следует повторить рас­четы при измененных величинах расходов жидкости в трубах:

Q ₁ + Q ₂ + Q ₅ = Q ₃ + Q ₄ + Q ₅ ± D Q.

Поправка D Q при этом выбирается удовлетворяющей уравне­нию

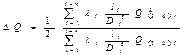
Если в процессе эксплуатации кольцевого трубопровода на линиях-отводах Q ₁, Q ₂, Q ₃, Q ₄ и Q ₅ изменяется сопротивление (закрывается задвижка), то соответственно этому сопротивлению происходит перераспределение расходов жидкости в отдельных отводах.

8.Неизотермическое течение жидкостей в трубопроводе. Расчет трубопроводов при неизотермическом течении жидкости

1 – изотермическое ламинарное течение; 2 – нагревание вязкой нефти; 3 – охлаждение вязкой нефти.

Закон распределения температуры жидкости по длине трубопровода получен Жуковым в 1883 г., в основу которого заложена потеря теплоты от элементарного участка dx в единицу времени в ОС: (1), где 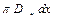- поверхность охлаждения элементарного участка, м³, 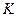- полный коэффициент теплоотдачи от жидкости в ОС, Вт/м²*⁰С, t – текущая температура жидкости.

При движении жидкости через рассматриваемый участок dx, жидкость охлаждается на dt ⁰С и теряет количество теплоты: 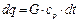(2), где 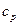- теплоемкость, Дж/кг*⁰С, G – массовый расход, кг/с. (1)=(2): 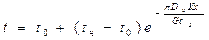- уравнение Шухова (закон распределения температуры жидкости по длине трубопровода).

В 1923 г. Лейбензон внес поправку в эту формулу, учтя работу трения потока жидкости, превращающуюся в теплоту, участвующую в тепловом балансе трубопровода: 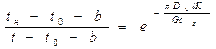; 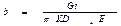- поправка Лейбензона, 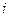- средний гидравлический уклон; Е – механический эквивалент теплоты (1 ккал=427 кгс*м=427*9,81 Н*м).

Закон изменения температуры на участке трубопровода, где происходит кристаллизация парафина, описывается формулой Черникина: 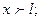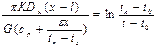; 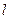- расстояние, на котором температура падает от t_н до t_п, 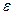- количество парафина, выделяющегося из нефти при понижении температуры от t_п до t 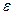(доли единицы); 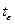- любая температура, для которой известно 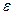; x – скрытая теплота кристаллизации парафина.

9.Гидравлический расчет трубопроводов, транспортирующих вязкопластичные жидкости.

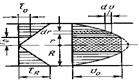
распреде­ление скоростей и напряжений в структурированном потоке.

Согласно закону Ньютона о вязкостном трении при движении жидкости в круглой трубе, уравнение касательного напряжения сдвига t записывается в следующем виде:

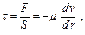
Парафинистые и застывающие нефти при понижении температуры приобретают вязкопластичные свойства вследствие образования в них пространственной структуры. В этом случае течение нефтей не начнется до тех пор, пока не будет достигнуто предельное напряжение сдвига, необходимое для разрушения пространственной структуры, и только после начала течения наблюдается пропорциональность между градиентом скорости и разностью напряжения τ-τ₀.

Таким образом, поведение вязкопластичных жидкостей отклоняется от закона Ньютона и описывается уравнением Шведова-Бингама: τ= τ₀+μ_{пл 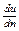,} где τ₀-предельное напряжение сдвига, μ_пл-пластичная вязкость; du/dn-градиент скорости сдвига.

Профиль скоростей при движении вязкопластичной жидкости в круглой трубе существенно отличается от профиля скорости ньютоновской жидкости. Так как напряжение сдвига убывает от стенки трубы и оси, на некотором радиусе r₀ напряжение сдвига становится равным предельному напряжению сдвига τ₀, и жидкость в цилиндре радиусом r₀ движется в виде «ядра», внутри которого скорость по сечению не изменяется. Радиус цилиндрического ядра r₀ определяют по формуле: r₀ = τ₀ 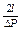. При ламинарном течении вязкопластичных жидкостей в трубах расход определяют по уравнению Букингема:

,

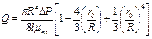которое также можно записать

.

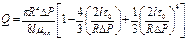Для упрощения расчетов применяют формулу Стокса: λ=64/Re_*, где Re_* - обобщенный параметр Рейнольдса, который вводится с использованием уравнения Букингема в виде: ,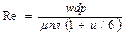

где u-параметр пластичности,

.

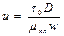При турбулентном движении парафинистых нефтей, являющихся вязкопластичными жидкостями, λ не зависит от Re. Численное значение λ в турбулентном режиме в зависимости от содержания парафина изменяется от 0,028 до 0,038, причем λ возрастает с ростом концентрации твердого парафина.

10.Гидравлический расчет трубопроводов для нефтяных эмульсий

Устойчивые высокодисперсные эмульсии ведут себя как однородные жидкости, и поэтому гидравлический расчет трубопроводов в этом случае не отличается от гидравлического расчета простого нефтепровода. Различие гидродинамического поведения неустойчивых и устойчивых эмульсий проявляется в эффекте гашения турбулентных пульсаций дисперсионной среды каплями дисперсной фазы. С учетом этого эффекта λ неустойчивых эмульсий определяется:

λ_э=64/Re_*э,Re<=2320,

,

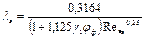2320< Re_*э<10⁵,

где Re_{*э-число} Рейнольдса, определяемое по формуле:

,

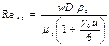где γ₀ указывает, является ли неустойчивая эмульсия ньютоновской или неньютоновской жидкостью, ее определяют по выражению:

,

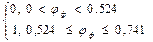1-ньютоновская

2- неньютоновская

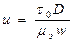-параметр пластичности,

w-средняя скорость течения, ρ_э, μ_э-плотность и вязкость эмульсии; D-внутренний диаметр трубопроводада; τ₀- дополнительное напряжение сдвига плотной эмульсии: τ₀=(0,195φ_ф-0,102)σ/d, где σ-межфазное натяжение; d-диаметр капель; φ_ф-содержание дисперсной фазы и эмульсии.

Плотная (устойчивая) эм-ия сущ-т при 0,524<φ_ф<0,741

Множитель (1+1,125*γ₁ *φ_ф)^-1 учитывает эффект гашения турбулентности.

Символ γ₁ указывает, проявляется ли в потоке неустойчивой эмульсии эффект гашения турбулентности, и определяется:

,

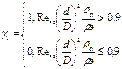где d-средний объемно-поверхностный диаметр капель неустойчивой эмульсии; d=1,4Dwe^0.6; We=σ/ρ_с число Вебера; ρ_с и ρ_ф-плотность дисперсной среды и дисперсной фазы.

Снижение давления при преодолении гидродинамического сопротивления при турбулентном течении неустойчивых эмульсий в промысловых трубопроводах зависит от содержания дисперсной фазы в неустойчивой эмульсии.

Содержание дисперсной фазы в эмульсии, при котором потери давления будут минимальны, является оптимальным.

1) Потери Р минимальны.

Оптимальное содержание дисперсной фазы в неустойчивой эмульсии определяют по формуле:

φ_ф0=0,68-0,4ρ_ф/ρ_с, 0,6< ρ_ф<1.4.

2) Потери Р для эм-ии не превышают потерь Р для нефти.

Важное значение для нефтепромысловой практики имеет определение области, в которой перепад давления при течении эмульсии не превышает перепада давления при течении нефти с той же скоростью. Эта область при 1< ρ_ф/ ρ_c<1.4 описывается формулой: φ_ф*=1,2-0,7 ρ_ф/ ρ_с.

3) Потери Р для эм-ии меньше чем потери Р для нефти.

Т.о., при 0< φ_ф< φ_ф* перепад давления в труб-де меньше, чем для чистой нефти. За пределами этой области перепад давления для эмульсии превышает перепад давления для чистой нефти.

Дата добавления: 2015-07-13