Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня

ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня
При потере устойчивости сжатого стержня изгиб стержня происходит в плоскости …

			наименьшей жесткости
			наибольшей жесткости
			равнонаклоненной к осям симметрии
			расположенной в любом направлении

Решение:

Рассмотрим прямолинейный стержень прямоугольного сечения с размерами 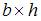, причем Пусть стержень сжимается силами F, приложенными строго в центре тяжести сечений. Изгиб стержня происходит в плоскости минимальной жесткости, то есть перемещения w направлены перпендикулярно той главной центральной оси, относительно которой осевой момент инерции сечения принимает минимальное значение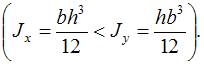

ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня
Нагрузка, превышение которой вызывает потерю устойчивости первоначальной формы тела, называется …

			критической
			предельной
			разрушающей
			динамической

Решение:

Устойчивость первоначальной формы равновесия тела зависит от величины приложенных к нему нагрузок. В случае, когда сила, сжимающая стержень, невелика, первоначальная прямолинейная форма равновесия не меняется, то есть устойчива (рис. а). При увеличении силы будет достигнуто состояние безразличного равновесия, при котором наряду с прямолинейной формой стержня возможны смежные, слегка искривленные формы равновесия (рис. б). В дальнейшем при самом незначительном увеличении нагрузки характер деформации стержня резко меняется – стержень выпучивается, теряет устойчивость (рис. в). Нагрузка, превышение которой вызывает потерю устойчивости первоначальной формы тела, называется критической.

ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня
Стержень длиной l сжимается силой F. Напряжения в стержне не превышают предела пропорциональности. При уменьшении длины стержня в два раза, критическое напряжение ___ раза.

			увеличивается в 4
			увеличивается в 2
			уменьшается в 2
			уменьшается в 4

Решение:
Для определения критического напряжения, когда напряжения в стержне не превышают предела пропорциональности, воспользуемся формулой 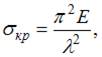где
При уменьшении длины стержня в два раза, при прочих равных условиях, гибкость стержня уменьшается в два раза. Критическое напряжение увеличивается в четыре раза.

ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня

Стержень большой гибкости круглого поперечного сечения диаметром , длиной 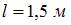нагружен силой F. Модуль упругости материала стержня 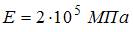. Схема закрепления стержня показана на рисунке.
Значение критического напряжения равно _______ МПа. При расчете принять .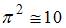

Решение:
Учитывая, что стержень имеет большую гибкость, для определения критического напряжения используем формулу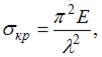
где − гибкость стержня.
При данных условиях закрепления стержня 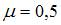. Радиус инерции
После вычислений получим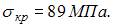

ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня
Стержень квадратного сечения площадью поперечного сечения А, длиной l сжимается силой F. При замене квадратного сечения на круглое с той же площадью А, при прочих равных условиях, гибкость стержня ______________ раза.

			увеличится в
			уменьшится в
			уменьшится в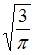
			увеличится в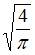

Решение:
Воспользуемся формулой для определения гибкости
При прочих одинаковых условиях, гибкость стержня зависит от минимального радиуса инерции сечения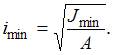
Для квадратного сечения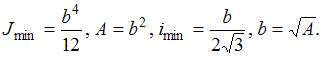
Для круглого сечения
После вычислений получим, что при замене квадратного сечения на круглое при одинаковой площади гибкость стержня увеличится в раза.

ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня

Стержень длиной 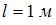круглого сечения диаметром нагружен силой F. Схема закрепления стержня показана на рисунке. Значение гибкости стержня равно …

Решение:
Гибкость стержня определяется по формуле
где 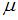− коэффициент приведения длины, учитывающий условия закрепления стержня; 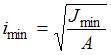– минимальный радиус инерции поперечного сечения.
При данном закреплении стержня 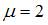. Минимальный радиус инерции для круглого сечения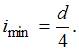
Подставляя значения 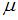, , 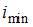в формулу для определения гибкости стержня, получим

После вычислений получим, что при замене квадратного сечения на круглое при одинаковой площади гибкость стержня увеличится в раза.

ЗАДАНИЕ N 7 сообщить об ошибке
Т ема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня
Свойство системы сохранять свое состояние при внешних воздействиях называется …

			устойчивостью
			жесткостью
			упругостью
			твердостью

Решение:
Пусть на прямолинейный стержень действуют сжимающие силы. При определенном значении силы F стержень не может сохранить первоначальную прямолинейную форму и неминуемо изогнется, как показано на рисунке.

Свойство системы сохранять свое состояние при внешних воздействиях называется устойчивостью.

ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня

Стержень квадратного сечения с размерами , длиной l сжимается силами F. При увеличении каждой стороны квадрата в два раза, при прочих равных условиях, гибкость стержня ___ раза.

			уменьшится в 2
			увеличится в 4
			уменьшится в 4
			увеличится в 2

Решение:
Гибкость стержня определяется по формуле При увеличении размеров поперечного сечения, при прочих равных условиях, гибкость будет зависеть от минимального радиуса поперечного сечения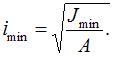
В первом варианте
во втором –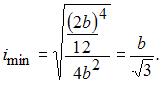
Следовательно, во втором варианте гибкость стержня уменьшится в два раза.

ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня
Стержень длиной l круглого сечения диаметром d сжимается силой F. Напряжения в стержне не превышают предела пропорциональности. При увеличении диаметра в два раза, при прочих равных условиях, критическое напряжение ____________ раза.

			увеличится в 4
			увеличится в 2
			уменьшится в 2
			уменьшится в 4

Решение:
Критическое напряжение в сжатом стержне, если напряжение в стержне не превышает предела пропорциональности, определяется по формуле
где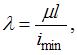
Для круглого стержня
При увеличении диаметра в два раза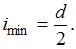
Следовательно, при увеличении диаметра стержня в два раза критическое напряжение увеличится в четыре раза.

Дата добавления: 2015-07-13