
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Построение нечеткой базы знаний
|
|
|
|
Рассмотрим представление объектов с использованием нечетких баз знаний. Объект с одни выхоом и n входами может быть представлен в общем виде уравнением вида: y = fy(x1,x2,…,xn). Переменные х и у могут быть как количественными, так и качественными. Количественные переменные характеризуются известными областями определения: U i=[ 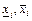 ], i =
], i = 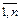 , где
, где 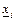 (
(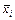 ) –нижнее (верхнее)значение выходной переменной xi.
) –нижнее (верхнее)значение выходной переменной xi.
Качественные значения х и у характеризуются множеством всех возможных значений:
U i ={ 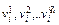 }, i =
}, i = 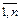 , например, U i = СКОРОСТЬ,
, например, U i = СКОРОСТЬ, 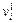 = низкая,…,
= низкая,…, 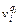 = высокая; Y ={
= высокая; Y ={ 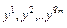 };
}; 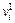 (
(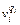 ) – балльная оценка соответствующая минимальному (максимальному) значению входной переменной xi;
) – балльная оценка соответствующая минимальному (максимальному) значению входной переменной xi; 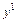 (
(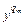 ) - балльная оценка соответствующая минимальному (максимальному) значению выходной переменной y; qi, i =
) - балльная оценка соответствующая минимальному (максимальному) значению выходной переменной y; qi, i = 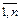 , qm- мощности множеств, причем в общем случае
, qm- мощности множеств, причем в общем случае 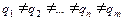 .
.
Для установления зависимостей между входами и выходом объекта рассмотрим их как лингвистические переменные, заданные на соответствующих универсальных множествах U i и Y.
Для оценки лингвистических переменных будем использовать качественные термы из следующих терм-множеств 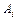 :
: 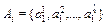 - терм множество переменной xi, i = 1,n;
- терм множество переменной xi, i = 1,n; 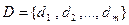 - терм-множина змінної y, де:
- терм-множина змінної y, де: 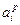 - р-й лингвистический терм переменной xi, p =1,li, i = 1,n; dj – j -й лингвистический терм переменной у; m – количество возможных различных значений y в установленной области ее значений. Мощности терм-множеств Ai в общем случае могут быть разными, т.е. l1
- р-й лингвистический терм переменной xi, p =1,li, i = 1,n; dj – j -й лингвистический терм переменной у; m – количество возможных различных значений y в установленной области ее значений. Мощности терм-множеств Ai в общем случае могут быть разными, т.е. l1 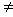 l2
l2 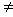 …
… 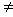 ln.
ln.
Якщо змінні xi, i = 1,n і y є кількісними, нечіткі

где 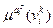 - степень принадлежности элемента
- степень принадлежности элемента 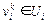 к терму
к терму 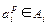 , p= 1 ,li, i= 1 ,n k= 1 ,qi, например
, p= 1 ,li, i= 1 ,n k= 1 ,qi, например 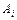 - СКОРОСТЬ,
- СКОРОСТЬ, 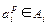 ={низкая, средняя, высокая, очень высокая}, то есть p= 1…4 (
={низкая, средняя, высокая, очень высокая}, то есть p= 1…4 (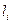 =4 - количество значений (термов) i -й лингвистичексой переменной), i= 1…3 (n =3 – количество лингвистичексих переменных),(СКОРОСТЬ, РАССТОЯНИЕ ДО ОБОЧИНЫ, РАССТОЯНИЕ ДО ПРЕПЯТСТВИЯ),
=4 - количество значений (термов) i -й лингвистичексой переменной), i= 1…3 (n =3 – количество лингвистичексих переменных),(СКОРОСТЬ, РАССТОЯНИЕ ДО ОБОЧИНЫ, РАССТОЯНИЕ ДО ПРЕПЯТСТВИЯ), 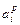 : НИЗКАЯ СКОРОСТЬ = (1/<40 км/час>, 0,6/<70 км/час>, 0,2/<90 км/час>); k= 1…10 (qi =10 – количество возможных значений входных переменных [10,20,...,100] (км/час), Наприклад,
: НИЗКАЯ СКОРОСТЬ = (1/<40 км/час>, 0,6/<70 км/час>, 0,2/<90 км/час>); k= 1…10 (qi =10 – количество возможных значений входных переменных [10,20,...,100] (км/час), Наприклад, 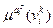 для терму
для терму 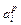 - низька швидкість лінгвістичної змінної
- низька швидкість лінгвістичної змінної 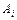 - швидкість і швидкості 50 км/год складе приблизно, 0,8.
- швидкість і швидкості 50 км/год складе приблизно, 0,8.
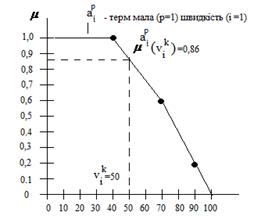
Аналогічно, вихідна змінна БЕЗОПАСНОСТЬ має терми dj: = (высокая, средняя, малая).
Предположим теперь, что для исследуемого объекта получено N экспериментальных данных, связывающих его входы и выход. Выборку можно упорядочить следующим образом: N = k1 + k2 + … + kj + … + km, где kj –количество экспериментальных данных соответствующих значению dj переменной у, 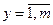 , m – общее количество значений выходной переменной. Будем считать, что N< l1 x l2 x … x ln, то есть количество имеющихся экспериментальных данных меньше полного перебора различных комбинаций возможных значений входных переменных объекта li, i = 1,n. Пронумеруем экспериментальную выборку следующим образом: 11,12…,1 k1 – номера комбинаций значений входных переменных, соответствующих значению выхода d1, m1,m2…,m km – номера комбинаций значений входных переменных, соответствующих значению выхода dm.
, m – общее количество значений выходной переменной. Будем считать, что N< l1 x l2 x … x ln, то есть количество имеющихся экспериментальных данных меньше полного перебора различных комбинаций возможных значений входных переменных объекта li, i = 1,n. Пронумеруем экспериментальную выборку следующим образом: 11,12…,1 k1 – номера комбинаций значений входных переменных, соответствующих значению выхода d1, m1,m2…,m km – номера комбинаций значений входных переменных, соответствующих значению выхода dm.
Сформируем так называемую матрицу знаний M = ||(n+1) x N ||, где (n+1) – количество столбцов матрицы, N –количество ее строк^
- первые n столбцовматрицы соответствуют входным переменным xi, i = 1,n, а последний столбец соответствует значениям dj выходной переменной, j=1,m;
- каждая строка матрицы представляет собой комбинацию значений входных переменных, отнесенную экспертом к одному из возможных значений выходной переменной у, при этом первые k1 строк соответствуют значению выходной переменной у=d1, следующие k2 строк значению у=d2 и т.д., а последние km
строк значению у=dm.
| Номер входной комбинации | Входные переменные | Выходная переменная | |||
| x1 | x2 | … xi… | xn | ||
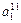
| 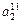
| … 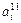 … …
| 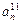
| d1 | |
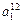
| 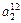
| … 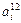 … …
| 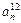
| ||
| … | … | … | … | … | |
| 1k1 | 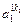
| 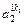
| … 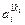 … …
| 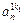
| |
| … | … | … | … | … | … |
| j1 | 
| 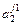
| … 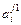 … …
| 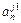
| dj |
| j2 | 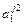
| 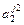
| … 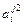 … …
| 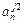
| |
| … | … | … | … | … | |
| J kj | 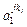
| 
| … 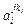 … …
| 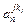
| |
| … | … | … | … | … | … |
| m1 | 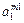
| 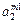
| … 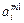 … …
| 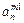
| dm |
| m2 | 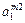
| 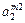
| … 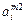 … …
| 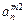
| |
| … | … | … | … | … | |
| M km | 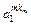
| 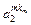
| … 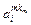 … …
| 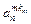
|
- элемент 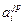 , который находится на пересечении i -го столбца и jp – строки, соответствует лингвистической оценке параметра xi в строке матрцы знаний с номером jp. Лингвистическая оценка
, который находится на пересечении i -го столбца и jp – строки, соответствует лингвистической оценке параметра xi в строке матрцы знаний с номером jp. Лингвистическая оценка 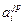 выбирается из терм-множества, соответствующего переменной xi, то есть
выбирается из терм-множества, соответствующего переменной xi, то есть 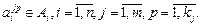
Данная матрица знаний определяет систему логических высказываний типа «ЕСЛИ-ТО, ИНАЧЕ», связывающих значения входных переменных с одним из возможных значений выхода. В части ЕСЛИ элементы строки соединяются по И, строки, соответствующие одному и тому же выходному значению – по ИЛИ, часть ТО соответствует значению выходной переменной, к части ИНАЧЕ относятся входные значения соответствующие другим выходным значениям выходной переменной:
ЯКЩО
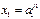 та
та 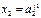 та … та
та … та 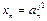 , або
, або
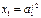 та
та 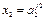 та … та
та … та  , або
, або
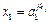 та
та 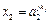 та … та
та … та 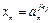 ,
,
ТО
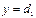 , ІНАКШЕ
, ІНАКШЕ
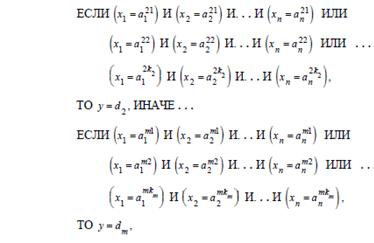
де 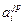 - лінгвістичний терм, що оцінює значення фактора xi в р–му рядку j–ої диз’юнкції, яка вибіроється з відповідної терм-множини Аі (
- лінгвістичний терм, що оцінює значення фактора xi в р–му рядку j–ої диз’юнкції, яка вибіроється з відповідної терм-множини Аі (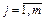 ,
, 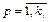 ,
, 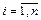 );
);
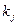 - кількість правил, що визначають значення вихідної змінної y=dj;
- кількість правил, що визначають значення вихідної змінної y=dj;
dj (j=1,m) - лінгвістична оцінка змінної y, яка визначається з терм-множини D.

Розглянемо аналітичну модель функції належності змінної х до довільного нечіткого терму Т у вигляді:

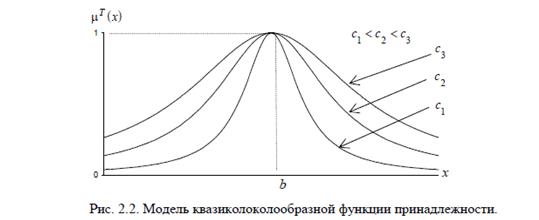

Пусть для объекта известно множество входных переменных Х, диапазоны количественного изменения каждой из входных переменных, функции принадлежности, которые позволяют представлять входные переменные в виде нечетких множеств, матрица знаний, как она определена ранее.
Отметим, что для объекта с непрерывным выходом интервал изменения ее значений разбивают на m подинтервалов: d1…dm.
Будем рассматривать лингвистические оценки 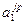 переменных x1…xn, входящих в логические высказывания, как нечеткие множества, определенные на универсальных множествах Ui=[
переменных x1…xn, входящих в логические высказывания, как нечеткие множества, определенные на универсальных множествах Ui=[ 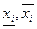 ],
], 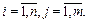 Введем обозначения:
Введем обозначения:
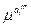 (xi), - функция принадлежности параметра xi
(xi), - функция принадлежности параметра xi 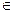 [
[ 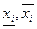 ] к нечеткому терму
] к нечеткому терму  ;
;
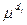 (x1, x2, …,xn) – функция принадлежности вектора входных переменных Х = (x1, x2, …,xn) значению выходной переменной y=dj,
(x1, x2, …,xn) – функция принадлежности вектора входных переменных Х = (x1, x2, …,xn) значению выходной переменной y=dj, 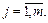
Тогда имеем два типа функций, связь между которыми определяется нечеткой базой знаний, на основе чего можно вывести следующую систему уравнений:
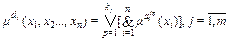
Представим теперь методику моделирования нелинейных объектов нечеткими базами данных в виде алгоритма, состоящего из пяти шагов:
- Зафиксировать вектор значений входных переменных
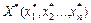 .
. - Задать функции принадлежности нечетких термов, используемых в нечеткой базе знаний и вычислить значение этих функций для заданных значений входных переменных.
- Согласно логическим уравнениям вычислить значения многомерных функций принадлежности
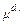
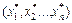 вектора
вектора 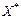 для всех значений dj,
для всех значений dj, 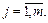 выходной переменной y.
выходной переменной y. - Для дискретного объекта искомым решением для вектора входных переменных
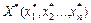 является значение
является значение 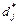 с максимальной функцией принадлежности:
с максимальной функцией принадлежности:
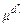
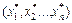 =
= 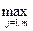 [
[ 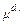
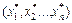 ].
].
В случае непрерывного объекта получим: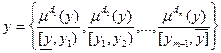 .
. - Для определения четкого числа соответствующего полученному в предыдущем уравнении нечеткому числу из интервала [
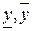 ], необходимо применить операцию дефаззификации, которая может быть определена следующим образом:
], необходимо применить операцию дефаззификации, которая может быть определена следующим образом:
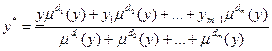 .
.
при вероятностной интерпретации степеней принадлежности данная формула может рассматриваться как аналог математического ожидания дискретной случайной величины. Если интервал [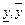 ] разбить на m равных отрезков, то есть:
] разбить на m равных отрезков, то есть: 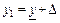 ,
, 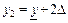 , …,
, …, 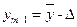 ,
, 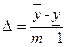 ,
,
то полученная выше формула упростится и примет вид, удобный для расчетов:
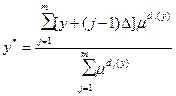 .
.
- Конец алгоритма.
|
|
|
|
|
Дата добавления: 2015-07-13; Просмотров: 1216; Нарушение авторских прав?; Мы поможем в написании вашей работы!