При цилиндрическом фрезеровании

Силовые характеристики

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

1. Плосконосов В.Н. “Технология монолитного бетонирования в строительстве” Брест: изд. БГТУ, 2002г.

2. Методические указания по выполнению курсового проекта “Производство монолитных бетонных и железобетонных работ”- Брест, изд. БГТУ, 1991г.

3. Хаютин Ю.Г. Монолитный бетон. М. 1991г.

4. Евдокимов Н.И., Маукевич А.Ф., Сытник В.С. Технология монолитного бетона и железобетона М.: Высшая школа, 1980г.

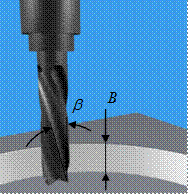
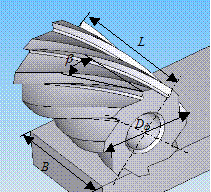
Фрезерование цилиндрическими фрезами является одним из распространенных видов обработки резанием деталей машин. Такой вид обработки применяют для формообразования плоских, цилиндрических, контурных поверхностей и т.п. Особую актуальность приобретают процессы формообразования контурных поверхностей на станках с ЧПУ концевыми фрезами (рис.3.1, а). Для цилиндрических и концевых фрез определяют основные геометрические параметры, среди которых диаметр D_ф фрезы и угол b наклона винтовой канавки (смотри рис.3.1). На режим резания влияют количество z зубьев и ширина B фрезерования. Зуб фрезы в нормальном сечении образует режущий клин, который характеризуется, по обыкновению, передним и задним углами (на рис.3.1 не показаны).

а) б)

Рис.3.1. Концевая (а) и цилиндрическая (б) фрезы

Исходя из того, что все силовые характеристики процесса фрезерования зависят, кроме режима резания, материала заготовки и других условий фрезерования, от срезаемого зубом фрезы слоя припуска, для определения соответствующей математической модели, прежде всего, необходимо рассмотреть кинематическую схему фрезерования.

Известно, что фрезерование цилиндрическими фрезами осуществляется за счет сочетания двух движений: вращательного вокруг оси фрезы – главное движение резания и поступательного в плоскости перпендикулярной оси фрезы – движение подачи. Благодаря этому любая точка лезвия зуба фрезы движется по траектории, которая является трохоидой (удлиненной циклоидой) в обращенной схеме, т.е. когда заготовка считается неподвижной. Такие траектории представлены в графическом окне интерфейса программы на рис.3.2. Обращаем внимание, что величина подачи на оборот специально выбрана слишком большой, для наглядности изображения. На рис.3.2 можно увидеть траектории движения шести зубьев фрезы (линии 1-6), которая имеет 12 зубьев. Расстояние между траекториями по горизонтали, т.е. в направлении подачи, является постоянной величиной в любом месте и равняется подаче S_z на зуб фрезы.

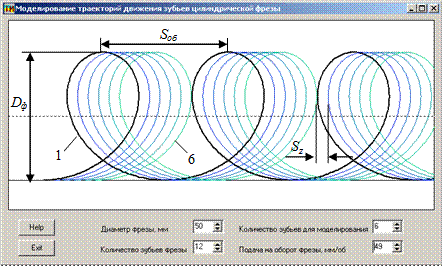
Рис.3.2. Интерфейс моделирования кинематики фрезерования

При реальном режиме фрезерования траектория точки зуба мало отличается от окружности, поэтому для упрощенного изображения кинематической схемы фрезерования можно воспользоваться схемой рис.3.3.

На схеме два положения исходной инструментальной поверхности фрезы отличаются на величину подачи на зуб (сравните с траекториями, которые изображены на рис.3.2). Размер срезаемого слоя припуска является глубиной H резания. В зависимости от направления векторов подачи S и скорости V резания различают встречное фрезерование (когда векторы направлены навстречу) и попутное фрезерование (когда направления векторов совпадают).

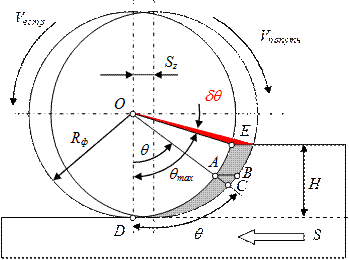
Рис.3.3. Схема расчета элементов резания

Зуб фрезы движется по поверхности резания, которая в сечении, перпендикулярном оси фрезы, представляется дугой (начало в точке D, конец в точке E), определяемой центральным углом q_max контакта:

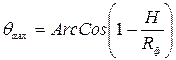
(3.1)

Текущее положение зуба фрезы можно определить текущим углом q контакта, а текущая толщина срезаемого слоя может быть найдена из геометрических соотношений треугольника АСВ. Если, с некоторым приближением, считать ∆АСВ прямоугольным, а Ð АВС» q, то толщина a срезаемого слоя равняется катету АС:

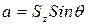
(3.2)

Поскольку на рис.3.3. изображено сечение фрезы независимо от ее продольной координаты, то форма поверхности резания и срезаемого одним зубом слоя припуска не зависит от угла наклона винтовой канавки, а соотношение (3.2) сохраняется для любой точки лезвия.

При любом методе фрезерования цилиндрическими или концевыми фрезами процесс резания характеризуется некоторыми существенными отличиями, среди которых можно выделить следующие:

- каждый зуб фрезы за один оборот часть времени выполняет резание, часть - холостой ход, который обусловливает циклическую прерывистость резания;

- происходит непрерывное изменение толщины срезаемого одним зубом слоя припуска при его перемещении по поверхности резания;

- при угле наклона режущего лезвия зуба фрезы, отличного от нуля, толщина срезаемого слоя припуска по длине лезвия является переменной;

- рабочая длина лезвия, т.е. его часть, которая срезает припуск, является также переменной величиной.

На рис.3.4. представлена схема определения составляющих силы резания при встречном и попутном фрезеровании. Сила резания (ее вектор на схеме не показан) раскладывается на составляющую P_xz, которая действует в плоскости, перпендикулярной оси фрезы, и составляющую P_y, действующую в направлении оси фрезы.

а) б)

Рис.3.4. Схема разложения силы резания на составляющие:

а) - встречное фрезерование, б) - попутное фрезерование

Составляющая P_xz силы резания может быть разложена двумя способами: по отношению к фрезе, которая вращается и по отношению к неподвижной системе координат XYZ. В первом случае:

,

где - окружная составляющая силы резания, - радиальная составляющая силы резания. Окружная составляющая считается главной составляющей силы резания, поскольку именно она создает крутящий момент резания и определяет эффективную мощность резания. Во втором случае:

,

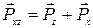где 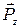- составляющая силы резания, которая действует в направлении оси Z, 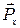- составляющая силы резания, действующая в направлении оси X. Такое разложение используют для определения влияния силы резания на точность обработки, поскольку именно эти составляющие вызывают упругие деформации технологической обрабатывающей системы по осям Z и X, являющиеся составляющими общей погрешности обработки.

Учитывая особенности процесса резания при фрезеровании цилиндрическими фрезами, стараются построить такую математическую модель, которая отображает существенную нестационарность процесса. В таком смысле подходит модель, построенная, исходя из удельной силы p резания, которая определяется по формуле:

,

(3.3)

где C_p и k – коэффициент и показатель степени, зависящие от механических свойств обрабатываемого материала, C_b – коэффициент, который учитывает влияние угла b наклона винтовой канавки фрезы, a – толщина срезаемого одним зубом слоя припуска. Следует отметить, что влияние угла наклона незначительное, так, при b <50⁰ коэффициент C_b равняется единице [1].

Для определения окружной составляющей силы резания удобно воспользоваться схемой рис.3.5, где представлена развертка поверхности резания. Окружная составляющая силы резания через удельную силу резания определяется по схеме рис.3.5 следующим образом:

.

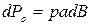(3.4)

Из геометрических соотношений схемы рис.3.5, а именно, из ∆АСВ можно записать:

,

(3.5)

где q₁, q₂ – начальный и конечный углы контакта соответственно. q=q₂-q₁.

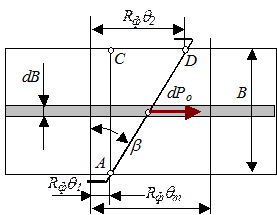
Рис.3.5. Схема определения окружной составляющей силы резания

Стремление получить аналитическую зависимость, пригодную для практического использования, привело к методике определения среднего значения силы резания через среднюю эффективную работу резания или эффективную мощность резания. При этом полностью теряется адекватность в смысле отображения реальной нестационарности процесса, но значительно упрощаются расчеты по формуле, которая содержит элементы режима резания, задаваемые на станке и подлежащие простому определению: подачу, глубину и ширину фрезерования.

При выводе формулы средней эффективной работы резания использовано то, что ее величина практически не зависит от угла наклона винтовой канавки [1,16].

Опираясь на зависимости (3.2), (3.3) и (3.4) можно определить окружную составляющую силы резания следующим образом:

.

(3.10)

Формула для определения среднего значения окружной составляющей силы резания будет иметь вид:

.

(3.16)

Приведенные выше теоретические материалы показывают, что представленные формулы получены с определенными предположениями, имеют существенные недостатки и их применение в математической модели процесса фрезерования цилиндрическими фрезами не приводит к адекватности с реальным процессом.

Радикальным решением проблемы создания математической модели является применение численных методов, которые хорошо адаптированы к современной вычислительной технике. Для объяснения предложенного численного метода удобно воспользоваться схемой рис.3.6, где показано поперечное сечение положения одного зуба фрезы, которое характеризуется углом q.

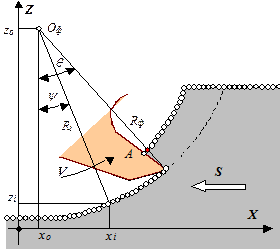
Рис.3.6. Схема определения толщины срезаемого слоя

Сечение поверхности резания представляется дискретной геометрической моделью (сечение условно показано кружками на рис.3.6). Расчеты выполняются по алгоритму, блок-схема которого представлена на рис.3.7.

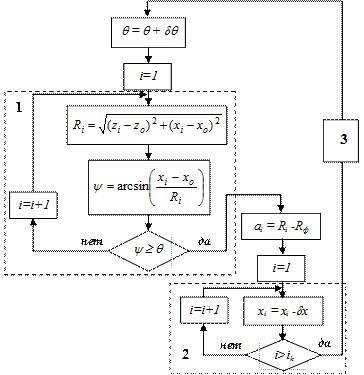
Рис.3.7. Блок схема алгоритма численного определения толщины

срезаемого слоя припуска

Группа операций, которая обведена пунктирным прямоугольником 1, образует замкнутый цикл поиска точки А. Поиск выполняется по операции сравнения углов y и q. Дальше, при выполнении условия выхода из цикла, рассчитывается толщина a срезаемого слоя.

Следующая группа операций, которая обведена пунктирным прямоугольником 2, выполняет замкнутый цикл, сдвигающий дискретную геометрическую модель в направлении подачи S. Цикл заканчивается при условии формирования всего массива данных, т.е. до номера i_к дискретной геометрической модели. Блок 3 выполняет перерасчет сечения поверхности резания с учетом найденной точки и алгоритм повторяется снова уже для следующего положения зуба фрезы, т.е. с шагом dq в направлении скорости резания V.

Элементарная величина окружной составляющей силы резания определяется по формуле (3.4), а вся окружная составляющая рассчитывается как сумма с учетом количества зубьев фрезы, которые режут и угла наклона винтовой канавки.

Предложенный алгоритм хорошо зарекомендовал себя при моделировании процесса цилиндрического фрезерования, как встречного, так и попутного.

Как уже отмечалось, процесс фрезерования цилиндрическими и концевыми фрезами характеризуется неравномерностью, для оценивания которой применяют коэффициент k_р неравномерности. Обычно коэффициент неравномерности определяют геометрическим соотношением:

.

(3.17)

где B – ширина фрезерования, h_o – осевой шаг винтовой канавки фрезы.

На основании анализа такого геометрического параметра делается вывод о равномерном фрезеровании, т.е. когда, по определению, сила резания должна быть постоянной. Реально равномерное фрезерование даже теоретически невозможно, так как всегда будет иметь место отклонение толщины срезаемого слоя, на выходе зуба фрезы из зоны резания (смотри рис.3.3). Об этом свидетельствует, прежде всего, практика и, во-вторых, результаты моделирования по разработанным численным методам определения толщины срезаемого слоя припуска.

Для оценивания неравномерности процесса фрезерования целесообразнее воспользоваться коэффициентом, который определяется из соотношения максимальной P_max и минимальной P_min величин силы резания согласно логическому смыслу понятия неравномерности:

.

(3.18)

Исследование силовых характеристик при цилиндрическом фрезеровании

Цель работы: Установить зависимости параметров срезаемого слоя припуска, условий фрезерования и окружной составляющей силы резания от режима резания и геометрических параметров фрезы.

Дата добавления: 2015-07-13