Решение. 1)Данныезначения для месячного уровня продаж уt образуют базовую линию, длины n =10

1)Данныезначения для месячного уровня продаж у_t образуют базовую линию, длины n =10. Для наглядности, изобразим данные задачи графически: на горизонтальной оси будем откладывать время t от 0 до 10, а на вертикальной оси уровни продаж у_t от 65 до 78. Для удобства построения вертикальную ось можно «разорвать».

Расположение точек на графике показывает, что они приблизительно выстраиваются вдоль некоторой прямой линии, что даёт возможность сделать предположение о линейной зависимости уровня продаж у_t от времени t: у_t = а _* t + b.

2) Для вычисления значений параметров уравнения регрессии a и b по формулам, указанным ранее, удобно построить расчётную таблицу. В первой колонке этой таблицы помещают время t, это порядковый номер месяцев от 1 до 10. Вторая колонка содержит соответственные значения базовых данных у_t. В третьей колонке расположены значения квадратов времени t ², а в четвёртой произведения соответственных значений t _* у_t. Внизу найдены суммы для первых четырёх колонок. С их помощью вычисляем все средние значения, необходимые для нахождения параметров a и b.

Остальные колонки расчётной таблицы будут заполняться позже.

	t	уt	t^2	t* уt	f(t)	│‌‌уt – f(t) │	Отнош.	(уt – f(t))^2
					65,71	0,71	0,011	0,50
					67,22	1,22	0,018	1,48
					68,73	0,27	0,004	0,07
					70,24	1,76	0,024	3,11
					71,75	1,25	0,017	1,57
					73,25	2,25	0,032	5,06
					74,76	1,24	0,016	1,53
					76,27	1,73	0,022	2,95
					77,78	0,78	0,010	0,61
					79,29	1,29	0,017	1,67
∑				4 112			0,172	18,62

Найдём все средние значения:

= ∑ t / n = 55/10 = 5,5; = ∑ y _t/ n = 725/10 = 72,5;

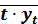= ∑ t ²/ n = 385/10 = 38,5; _.= (∑ t _* у _t)/ n = 4112/10 = 411,2.

Вычислим параметры уравнения регрессии, по формулам указанным выше:

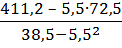= =1,51;

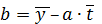= 72,5 – 1,51_*5,5 = 64,2.

В результате получим уравнение линейной регрессии:

f(t) = 1,51_* t +64,2.

Построим на графике найденное уравнение прямой по двум точкам:

при t = 0, f(0) = 11,51*0 + 64,2 = 64,2; это точка (0; 64,2);

при t = 10, f(10) = 1,51*10 + 64,2 = 15,1 + 64,2 = 79,3; это точка (10; 79,3). Отметим эти точки на графике (они отмечены крестиками) и проведём через них прямую линию. Это и есть прямая регрессии. Наблюдаемые точки (t; y _t) лежат по обе стороны от прямой регрессии и в совокупности наилучшим образом приближены к ней. Обратите внимание, что точка с координатами (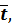 , обязательно должна лежать на прямой регрессии. В рассматриваемой задаче это точка (5,5; 72,5), она действительно лежит на прямой.

3) Оценим адекватность полученной модели, то есть насколько хорошо регрессионные значения f(t) приближены к данным фактическим значениям у _t.. Это можно сделать с помощью характеристики, называемой «средняя ошибка аппроксимации». Она ‌‌вычисляется по формуле:

А = (1/ n) ∑(‌‌‌│ у _t – f(t) │/ y _t).

Чем меньше средняя ошибка аппроксимации, тем выше качество регрессионной модели. Допустимый предел ошибки не более 10%.

‌ Используя найденное уравнение регрессии, вычислим значения у для всех значений t от 1 до 10: f(1) =1,51_*1+64,2 = 65,71; f(2) =1,51_*2+64,2 = 67,22 и т. д. Поместим эти значения в пятую колонку расчетной таблицы под заголовком f(t). Следующая шестая колонка содержит отклонения данных значений y_t от значений, вычисленных по уравнению регрессии f(t), взятые по абсолютной величине: │ у _t – f(t) │. В следующей седьмой колонке вычислим отношения найденных отклонений к соответствующим фактическим значениям y_t: │ у _t – f(t) │/ y _t. Далеенайдём итоговую сумму этих отношений. Полученное значение суммы делим на объём выборки n = 10. Найденное значение и есть ошибка аппроксимации. В решаемой задаче А = = 0,172/10 = 0,0172, то есть А = 1,72%. Ошибка значительно меньше допустимого значения 10%, следовательно найденная регрессионная модель адекватна и её можно использовать для прогнозирования.

4) Сделаем прогноз на следующие два месяца одиннадцатый и двенадцатый:

у ₁₁ = f (11) = 1,51_*11 + 64,2 = 80,80;

у ₁₂ = f (12) = 1,51_*12 + 64,2 = 82,31.

На графике эти значения отмечены жирными точками на прямой регрессии, они соответствуют значениям времени t =11 и t =12.

5) Найденные прогнозные значения являются усреднёнными. В действительности можно прогнозировать лишь попадание прогнозных значений в некоторый доверительный интервал. Уровень доверия по условию задачи равен 90%.

Ошибка прогноза Δ вычисляется по формуле: Δ = 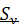_*T_*K_m, где

– остаточное среднее квадратическое отклонение,

Т– квантиль распределения Стьюдента,

К _m – поправочный коэффициент, m = 1;2.

Для подсчёта остаточного среднего квадратического отклонения S _y заполним последнюю колонку расчётной таблицы. Для этого возводим в квадрат найденные ранее отклонения (в шестой колонке) и суммируем эти квадраты отклонений. Полученную сумму делим на число степеней свободы (n – k) = 10 – 2 = 8, где n =10 – длина базового периода, k =2 – количество параметров регрессионной модели (их два a и b). Остаточное среднее квадратическое отклонение вычисляется по формуле:

В рассматриваемой задаче:

Квантиль Т находится по таблице распределения Стьюдента. Он зависит от уровня надёжности р и числа степеней свободы (n – k).

Если р = 90%, а число степеней свободы n – k = 10-2= 8, то Т=1,86.

Поправочный коэффициент К_m вычисляется по специальной формуле и зависит от длины базового периода n и от глубины прогноза m.

Глубина прогноза отсчитывается, начиная от базового периода, длина которого n =10. Для прогноза на 11-ый месяц глубина m = 1 и поправочный коэффициент К₁ = 1,21. Для прогноза на 12-ый месяц глубина m = 2 и поправочный коэффициент К₂ = 1,27.

В результате получим следующие ошибки прогноза на 11-ый и 12-ый месяцы: Δ₁₁ = 1,53*1,86*1,21 = 3,44; Δ₁₂ = 1,53*1,86*1,27 = 3,60.

При увеличении глубины прогноза ошибка прогноза возрастает, поэтому прогноз выполняют на глубину не более четверти длины базового периода, то есть менее чем n /4.

6) Найдём относительную погрешность прогноза: δ_t = ( / y_t)_*100%. Если относительная ошибка не более 10%, то точность прогноза высокая, если от 10% до 20%, то точность хорошая; если от 20% до 50%, то точность удовлетворительная, иначе точность неудовлетворительная.

В данной задаче δ₁₁ = Δ₁₁ / у ₁₁ = 3,44/80,80 = 0,0425, т. е. 4,25%,

δ₁₂ = Δ₁₂ / у ₁₂ = 3,60/82,31 = 0,0438, т. е. 4,38%,

это означает, что точность прогноза высокая.

Результаты прогноза записывают в виде доверительного интервала:

y _t. Є (f(t) – ; f(t) _.+ ) с вероятностью р; t =11 и t = 12. Чем выше вероятность р, тем шире интервал для прогнозирования и, следовательно, точность хуже.

В решаемой задаче с вероятностью 90%:

у ₁₁Є (80,80 – 3,44; 80,80 + 3,44) = (77,36; 84,24),

у ₁₂Є (82,31 – 3,60; 82,31 + 3,60) = (78,71; 85,91).

Ответ. Линейная трендовая модель для прогнозирования имеет вид:

y = 1,51_* t +64,2.

Прогноз продаж на 11-ый месяц: 80,80 ± 3,44; на 12-ый месяц: 82,31 ± 3,60

с надёжностью 90%. Модель адекватная, точность прогноза высокая.

Тема 2. Системы массового обслуживания (СМО)

СМО – это системы, где многократно повторяются одни и те же однотипные процессы, связанные с обслуживанием (склады, магазины, автозаправки, ремонтные мастерские, телефонные сети и т. п.). Основные составляющие СМО: канал обслуживания (грузчик, кассир, ремонтная бригада, телефонный аппарат и т. п.) и поток требований или заявок (покупатели, клиенты, абоненты и проч.).

Канал обслуживания характеризуется двумя параметрами: t _{обсл .}– среднее время обслуживания одного требования одним каналом; μ – интенсивность обслуживания, это количество требований, обслуживаемых одним каналом в ед. времени. Связь между ними: μ = 1/ t _{обсл .}; t _{обсл .}=1/ μ.

Требования (заявки) характеризуются также двумя параметрами: Т – среднее время между двумя последовательными заявками; λ – интенсивность поступления заявок, это количество заявок, поступающих в ед. времени. Связь между ними: λ = 1/Т; Т = 1/ λ.

Параметр загрузки ρ = λ/μ – важнейшая характеристика СМО, показывает соотношение интенсивности поступления требований с интенсивностью их обслуживания.

СМО может иметь несколько каналов обслуживания. Обычно считают, что интенсивность обслуживания у них одинаковая. По количеству каналов различают:

– одноканальные СМО, имеющие один канал обслуживания (n =1);

– многоканальные СМО, когда каналов обслуживания два и более (n ≥2).

По наличию очереди различают следующие виды СМО: с отказом (без очереди); с ожиданием (очередь неограниченная); смешанного типа (очередь ограничена).

В дальнейшем будут рассматриваться системы Марковского типа. Отличительным свойством таких систем является отсутствие последействия: будущее системы зависит только от её состояния в данный момент и не зависит от того, что было до этого момента. Поток заявок при этом называется простейшим. Для систем такого типа имеются математические модели, одной из которых мы и воспользуемся ниже для решения задачи.

Задача 11–21. Отгрузка производится со склада имеющего n погрузочных площадок. На склад для погрузки поступает простейший поток грузовиков с интенсивностью λ машин в час. Среднее время погрузки одной машины составляет t_обсл минут. Если все погрузочные площадки заняты, то грузовики становятся в очередь.

n = 4; λ = 9 маш./час; t_обсл. = 24 мин.; к =2.

1) Укажите вид системы обслуживания.

2) Определите интенсивность обслуживания и параметр загрузки системы.

3) Сколько погрузочных площадок должен иметь склад, чтобы очередь не была бесконечной? Выполняется ли это условие для данной СМО?

4) Перечислите возможные состояния СМО и найдите соответствующие им вероятности.

5) Найдите вероятность того, что очереди нет.

6) Какова вероятность наличия очереди?

7) Какова вероятность того, что в очереди не более «k» грузовиков? Более чем «k» грузовиков?

8) Найдите среднее количество грузовиков в очереди.

9) Каково среднее число грузовиков на обслуживании?

10) Каково среднее число грузовиков на складе?

11) Укажите среднее время пребывания грузовика в очереди.

12) Найдите среднее время пребывания грузовика на складе.

Оцените работу склада с помощью показателей эффективности, найденных в пунктах 5 – 12.

Дата добавления: 2015-08-31