Решение. Элементы заданной платёжной матрицыАозначают, что если первый игрок выберет стратегию А1, а второй игрок применит стратегию В1

Элементы заданной платёжной матрицы А означают, что если первый игрок выберет стратегию А1, а второй игрок применит стратегию В1, то первый игрок А выиграет а ₁₁ = 7 ед., а второй игрок В проиграет эти 7 ед. Аналогично, если первый игрок выберет стратегию А1, а второй игрок выберет стратегию В2, то первый игрок А выиграет а ₁₂ = 2 ед., а второй игрок В проиграет 2 ед. Далее, если первый игрок выберет стратегию А2, а второй игрок выберет стратегию В1, то первый игрок А выиграет а ₂₁ = 4 ед., а второй игрок В проиграет 4 ед. И, наконец, если первый игрок выберет стратегию А2, а второй игрок выберет стратегию В2, то первый игрок А выиграет а ₂₂ = 9 ед., а второй игрок В проиграет эти 9 ед.

1) Пусть первый игрок А выбрал стратегию А1. Тогда он получит выигрыши либо 7, либо 2, в зависимости от того, какую стратегию выберет игрок В. Наименьший из выигрышей α1= min(7; 2) = 2 называется гарантированным (обязательным) выигрышем игрока А при выборе им стратегии А1. Аналогично при выборе игроком А стратегии А2 его гарантированный выигрыш составит α2= min(4; 9) = 4. Из гарантированных выигрышей игрока А выберем наибольший: α = max(α1; α2) = max(2; 4) = 4. Этот наибольший из гарантированных выигрышей игрока А называется нижней ценой игры: α = max(min a ij). Поведение игрока А, основанное на максимизации минимальных выигрышей, называется принципом максимина (maxmin).

Пусть второй игрок В выбрал стратегию В1. Тогда его проигрыши составят либо 7, либо 4, в зависимости от того, какую стратегию выберет игрок А. Наибольший из проигрышей β1 = max(7; 4) = 7 является наихудшим проигрышем игрока В при выборе им стратегии В1. Аналогично при выборе игроком В стратегии В2 его наихудший проигрыш составит β2= max(2; 9) = 9. Из наихудших проигрышей игрока В выберем самый маленький проигрыш: α = min(β1; β2) = min(7; 9) = 7. Этот наименьший из наибольших проигрышей игрока В называется верхней ценой игры: β = min(max a ij). Поведение игрока В, основанное на минимизации максимальных проигрышей, называется принципом минимакса (minmax).

Итак, нижняя цена игры α = 4, верхняя цена игры β = 7. Всегда α ≤ β.

Так как α ≠ β, то игра не решается в чистых стратегиях. То есть, нет такой чистой пары стратегий, применяя которые можно достичь наилучшего результата одновременно для обоих игроков.

2) Для любой матричной игры нижняя цена игры не превосходит верхней цены игры, то есть α ≤ β. Если α = β, то игра решается в чистых стратегиях, при этом цена игры υ = α = β. Это означает, что первый игрок А выиграет не менее υ, а второй проиграет не более υ ед.

Если α ˂ β, то решение игры в чистых стратегиях невозможно. В этом случае игру решают в смешанных стратегиях. Смешанная стратегия означает, что игрок А использует обе свои чистые стратегии, причём первую свою чистую стратегию А1 с вероятностью р1, а вторую чистую стратегию А2 с вероятностью р2. Очевидно, что при этом р1 ≥ 0, р2 ≥ 0 и р1 + р2 = 1.

Аналогично, второй игрок В также использует обе свои чистые стратегии, причём первую чистую стратегию В1 с вероятностью ԛ1, а вторую чистую стратегию В2 с вероятностью ԛ2. Очевидно, что при этом ԛ1 ≥ 0, ԛ2 ≥ 0 и ԛ1 + ԛ2 = 1. Таким образом, смешанные стратегии игроков задаются в виде векторов вероятностей р и ԛ.

Смешанная стратегия игрока А: р =( р1; р2 ), р1 ≥ 0, р2 ≥ 0 и р1+р2 = 1.

Смешанная стратегия игрока В: ԛ =( ԛ1; ԛ2 ), ԛ1 ≥ 0, ԛ2 ≥ 0 и ԛ1+ԛ2 = 1.

Любая матричная игра имеет оптимальное решение в смешанных стратегиях. Цена игры υ означает выигрыш игрока А, равный проигрышу игрока В и заключена между нижней и верхней ценой игры: α ˂ υ ˂ β.

3) Запишем данную задачу в виде:

Используя эту запись легко понять, что если второй игрок В применит свою чистую стратегию В1, то игрок А выиграет 7 ед. с вероятностью р1 и 4 ед. с вероятность р2, тогда ожидаемый средний выигрыш игрока А составит: (7_*р1 + 4_*р2), при этом он должен быть равен цене игры υ. Аналогично, если второй игрок В применит свою чистую стратегию В2, то средний ожидаемый выигрыш игрока А составит: 2_*р1 + 9_*р2, при этом он также равен цене игры υ.

Если первый игрок А применит свою чистую стратегию А1, то ожидаемый средний проигрыш игрока В будет: 7_*ԛ1 + 2_*ԛ2, при этом он равен цене игры υ. Аналогично, если первый игрок А использует свою чистую стратегию А2, то средний ожидаемый проигрыш игрока В составит: 4_*ԛ1+ 9_*ԛ2, и он также должен быть равен цене игры υ.

В результате математические модели задач для обоих игроков будут записаны в виде систем уравнений:

Игрок А

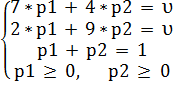
Игрок В

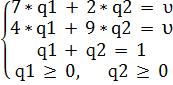
4) Для нахождения оптимальных стратегий игроков решим обе полученные модели, как системы трёх уравнений с тремя неизвестными: р1, р2, υ и q1, q2, υ. Для этого в обеих системах вычтем из первого уравнения второе, чтобы исключить неизвестное υ и, выразив из полученного соотношения одну вероятность через другую, подставим найденное выражение в третье уравнение.

5*р1 – 5*р2 = 0 3*q1 – 7*q2 = 0

5*p1= 5*p2 3*q1 = 7*q2

p1 = p2 q1 = (7/3)*q2

p2 +p2 = 1 (7/3)*q2 + q2 = 1

2*p2 = 1 (10/3)*q2 = 1

p2 = 1/2; p1 = 1/2; q2 = 3/10; q1 = 7/10;

υ = 7*р1 + 4*р2 = υ =7*q1 + 2*q2 =

=7*0,5+4*0,5 =5,5. = 7*0,7 + 2*0,3 =5,5.

Цена игры в обеих задачах должна быть одна и та же. У нас υ= 5,5, отметим, что она заключена между нижней и верхней ценой игры: α = 4 ˂ 5,5 ˂ 7 = β.

Ответ: р = (0,5; 0,5), ԛ = (0,7; 0,3), υ = 5,5.

Этот результат означает, что если при многократном повторении игры первый игрок будет применять свои чистые стратегии с вероятностями 50%, то он получит выигрыш не менее 5,5. Если при этом второй игрок, независимо от поведения первого, будет на 70% применять свою первую стратегию и на 30% вторую стратегию, то он проиграет не более 5,5 ед.

Тема 6. Сетевое планирование и управление (СПУ)

СПУ даёт методы планирования и управления большим комплексом связанных работ. Оно основано на моделировании процессов деятельности с помощью сетевых графиков.

Дата добавления: 2015-08-31