
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Множини міри нуль і вимірні функції 2 страница
|
|
|
|
Доведемо тепер властивість v), обернену до властивості iv).
Нам дано, що функції 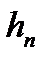 невід’ємні, монотонно спадають і що
невід’ємні, монотонно спадають і що 
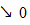 . Очевидно, що функції
. Очевидно, що функції 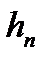 , спадаючи і залишаючись додатними, мають при
, спадаючи і залишаючись додатними, мають при 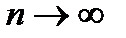 деяку границю
деяку границю 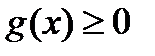 . Ми повинні довести, що функція
. Ми повинні довести, що функція  майже скрізь рівна нулеві. Для будь-якої функції
майже скрізь рівна нулеві. Для будь-якої функції 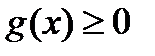 множина
множина  всіх точок, де вона відмінна від нуля, є зліченною сумою множин
всіх точок, де вона відмінна від нуля, є зліченною сумою множин 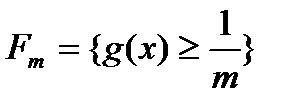 . Запис в правій частині рівності показує, що множина
. Запис в правій частині рівності показує, що множина 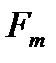 є множиною всіх точок, де
є множиною всіх точок, де 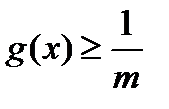 . Якщо ми покажемо, що в нашому випадку кожна із множин
. Якщо ми покажемо, що в нашому випадку кожна із множин 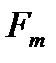 має міру нуль, то і їх сума
має міру нуль, то і їх сума  , за лемою 1, також буде мати міру нуль. Тому обмежимось дослідженням множини
, за лемою 1, також буде мати міру нуль. Тому обмежимось дослідженням множини 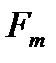 .
.
Досить розглянути ту частину 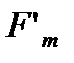 множини
множини 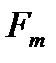 , де функції
, де функції 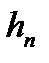 неперервні (інша частина зліченна і тому має міру нуль). Так як
неперервні (інша частина зліченна і тому має міру нуль). Так як 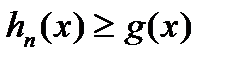 , то в кожній із точок множини
, то в кожній із точок множини 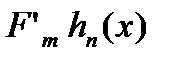 також
також 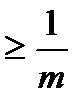 . Фіксуємо номер
. Фіксуємо номер 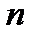 ; тоді ділянки сталості функції
; тоді ділянки сталості функції 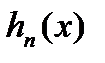 , які відповідають її значенням, більшим або рівним
, які відповідають її значенням, більшим або рівним 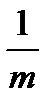 утворюють покриття множини
утворюють покриття множини 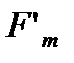 . Нехай
. Нехай  означає суму довжин цих ділянок. Так як
означає суму довжин цих ділянок. Так як 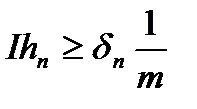 , то ми отримаємо, що
, то ми отримаємо, що 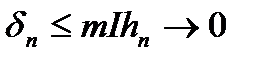 при
при 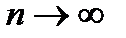 .
.
Таким чином, при достатньо великому 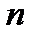 множина
множина 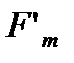 покривається системою інтервалів з класу східчастих функцій на більш ширший клас.
покривається системою інтервалів з класу східчастих функцій на більш ширший клас.
Нагадаємо схему побудови інтегралу Рімана. В цій схемі для побудови інтеграла від функції 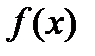 діють наступним чином. Розбивають відрізок
діють наступним чином. Розбивають відрізок 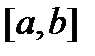 точками поділу
точками поділу 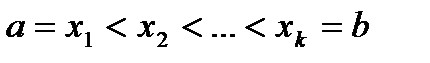 на частинні інтервали
на частинні інтервали 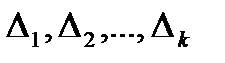 позначають
позначають 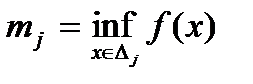 ,
, 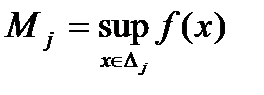
 і складають дві суми (залежні, звісно, від сукупності
і складають дві суми (залежні, звісно, від сукупності 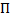 точок розбиття
точок розбиття 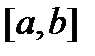 на частини):
на частини): 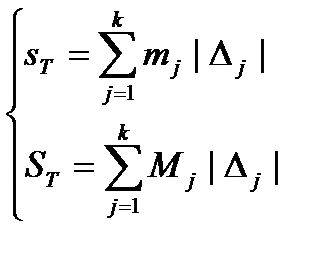 Перша сума називається нижньою, друга-верхньою. Якщо, додавши нові точки поділу, замінити розбиття
Перша сума називається нижньою, друга-верхньою. Якщо, додавши нові точки поділу, замінити розбиття 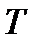 розбиттям
розбиттям 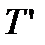 то
то 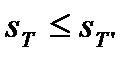 ,
,  . Звідси, фактично, слідує, що
. Звідси, фактично, слідує, що 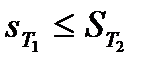 які б не були підрозбиття
які б не були підрозбиття 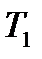 i
i 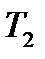 . Далі розглядається довільна послідовність розбиттів
. Далі розглядається довільна послідовність розбиттів 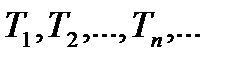 кожне з яких отримується внаслідок добавленням до попереднього нових точок поділу; тоді відповідні нижні і верхні суми утворюють монотонні послідовності, які йдуть назустріч одна одній:
кожне з яких отримується внаслідок добавленням до попереднього нових точок поділу; тоді відповідні нижні і верхні суми утворюють монотонні послідовності, які йдуть назустріч одна одній: 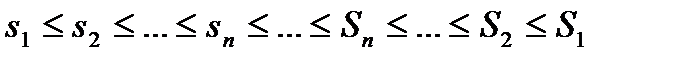 . Кожна із послідовностей має тому свою границю:
. Кожна із послідовностей має тому свою границю: 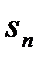
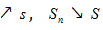 причому
причому 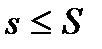 . Доводиться що числа
. Доводиться що числа 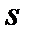 i
i 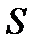 не залежать від вибору послідовності розбиттів
не залежать від вибору послідовності розбиттів  якщо тільки довжина максимального інтервалу в розбитті
якщо тільки довжина максимального інтервалу в розбитті 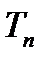 необмежено зменшується з ростом
необмежено зменшується з ростом 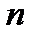 . Функція
. Функція 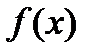 вважається інтегрованою за Ріманом, якщо
вважається інтегрованою за Ріманом, якщо 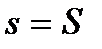 ; загальне значення цих границь і покладають рівним значенню інтегралу від
; загальне значення цих границь і покладають рівним значенню інтегралу від 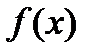 . Якщо ж
. Якщо ж  , то функцію
, то функцію 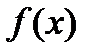 вважають неінтегровною за Ріманом. Розглянемо тепер цей процес з точки зору дій із східчастими функціями. Кожному розбиттю
вважають неінтегровною за Ріманом. Розглянемо тепер цей процес з точки зору дій із східчастими функціями. Кожному розбиттю 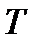 відрізка
відрізка 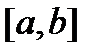 з точками поділу
з точками поділу 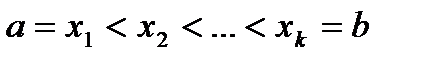 відповідають дві східчасті функції
відповідають дві східчасті функції 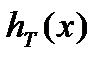 i
i 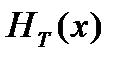 ; перша з них на інтервалі
; перша з них на інтервалі 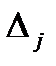 приймає значення
приймає значення 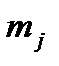 , а друга – значення
, а друга – значення 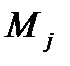
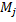 . Нижня і верхня суми представляють собою інтеграли від цих східчастих функцій. Послідовності розбиттів
. Нижня і верхня суми представляють собою інтеграли від цих східчастих функцій. Послідовності розбиттів  відповідають дві послідовності функцій
відповідають дві послідовності функцій 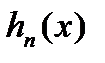 i
i 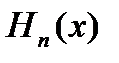 , перша з яких зростає, а інша спадає. Нехай, далі,
, перша з яких зростає, а інша спадає. Нехай, далі, 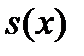 i
i 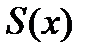 граничні функції цих послідовностей:
граничні функції цих послідовностей:

 ,
, 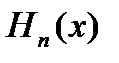
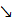
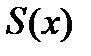 .
.
Так як, крім цього,  , то маємо що
, то маємо що  . Ми стверджуємо, що якщо функція
. Ми стверджуємо, що якщо функція 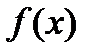 інтегрована за Ріманом, то ці три функції майже скрізь співпадають. Дійсно, різниця
інтегрована за Ріманом, то ці три функції майже скрізь співпадають. Дійсно, різниця 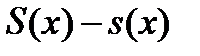 є границею послідовності невід’ємних східчастих функцій
є границею послідовності невід’ємних східчастих функцій 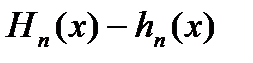 . Ця послідовність монотонно спадає, і в випадку інтегрування
. Ця послідовність монотонно спадає, і в випадку інтегрування 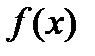 інтеграли від
інтеграли від 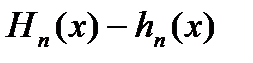 прямують до нуля. Але тоді, за властивістю v) послідовність
прямують до нуля. Але тоді, за властивістю v) послідовність 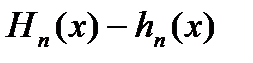 прямує до нуля майже скрізь. Тому в випадку інтегрованості
прямує до нуля майже скрізь. Тому в випадку інтегрованості 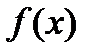 функції
функції 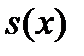 i
i 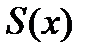 співпадають майже скрізь одна з одною і з функцією
співпадають майже скрізь одна з одною і з функцією 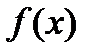 . Ми бачимо, що функція інтегрована за Ріманом, є одночасно границею (майже скрізь) зростаючої послідовності східчастих функцій
. Ми бачимо, що функція інтегрована за Ріманом, є одночасно границею (майже скрізь) зростаючої послідовності східчастих функцій 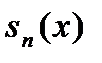 і спадної послідовності східчастих функцій
і спадної послідовності східчастих функцій 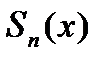 ; а інтеграл цієї функції є границею інтегралів східчастих функцій, які беруть участь у вказаних послідовностях.
; а інтеграл цієї функції є границею інтегралів східчастих функцій, які беруть участь у вказаних послідовностях.
І навпаки, якщо функції 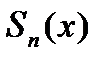 i
i 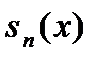 збігаються майже скрізь до
збігаються майже скрізь до 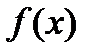 ,то різниця
,то різниця  , співпадаючи, майже скрізь прямує до нуля. Тому, згідно з властивістю iv), ми маємо
, співпадаючи, майже скрізь прямує до нуля. Тому, згідно з властивістю iv), ми маємо 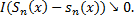 Звідси випливає, що числові послідовності
Звідси випливає, що числові послідовності 
 ,
, 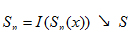

Мають спільну границю. А це і означає, що функція 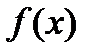 інтегрована за Ріманом.
інтегрована за Ріманом.
Таким чином, функція 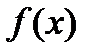 інтегрована за Ріманом тоді і тільки тоді, коли вона є границею (в розумінні збіжності майже скрізь) деякої зростаючої послідовності східчастих функцій
інтегрована за Ріманом тоді і тільки тоді, коли вона є границею (в розумінні збіжності майже скрізь) деякої зростаючої послідовності східчастих функцій 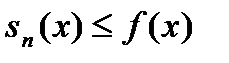 і одночасно границею деякої послідовності східчастих функцій
і одночасно границею деякої послідовності східчастих функцій 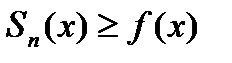 ; при цьому інтеграл від
; при цьому інтеграл від  є загальним значенням границь інтегралів від функцій
є загальним значенням границь інтегралів від функцій 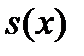 i
i 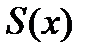 . Це спостереження буде слугувати нам опорою при розширенні визначення інтегралу на більш ширший клас функцій.
. Це спостереження буде слугувати нам опорою при розширенні визначення інтегралу на більш ширший клас функцій.
Введемо клас функцій, який будемо позначати 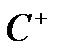 :
:
Функція 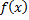 належить до класу
належить до класу 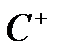 , якщо вона може бути представлена як границя (в розумінні збіжності майже скрізь) монотонно зростаючої послідовності східчастих функцій
, якщо вона може бути представлена як границя (в розумінні збіжності майже скрізь) монотонно зростаючої послідовності східчастих функцій 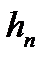
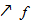
Причому інтеграли від цих функцій обмежені в сукупності:
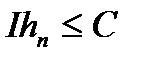
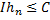 .
.
Теорема 2.2. Довільна функція 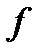 із класу
із класу 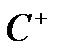 майже скрізь скінченна. Доведення. Нехай
майже скрізь скінченна. Доведення. Нехай 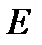 множина точок, де
множина точок, де 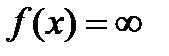 . Можна вважати наперед, що в кожній точці множини
. Можна вважати наперед, що в кожній точці множини 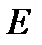 всі функції
всі функції 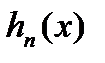 неперервні і виконується співвідношення
неперервні і виконується співвідношення 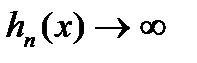 . Виберемо довільно число
. Виберемо довільно число 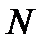 ; в кожній із точок множини
; в кожній із точок множини 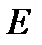 , починаючи з деякого номера, виконується нерівність
, починаючи з деякого номера, виконується нерівність  . Так що
. Так що 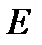 покривається скінченною сумою множин вигляду
покривається скінченною сумою множин вигляду 
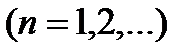 . Кожна із цих множин представляє собою скінченне число інтервалів; тому їх об’єднання також є скінченною сумою інтервалів:
. Кожна із цих множин представляє собою скінченне число інтервалів; тому їх об’єднання також є скінченною сумою інтервалів: 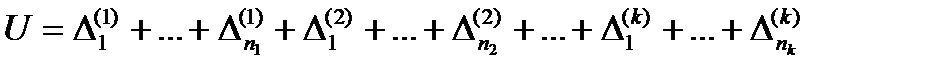 .
.
Тут через 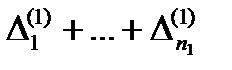 позначенні інтервали множини
позначенні інтервали множини  ; через
; через  інтервали множини
інтервали множини 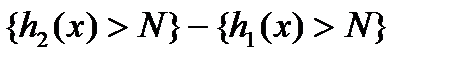 так що,
так що, 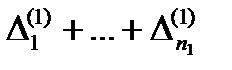 ,
,  утворюють множину
утворюють множину 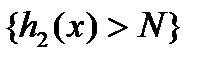 і так далі. Оцінимо суму довжин всіх цих інтервалів. Для цього введемо позначення:
і так далі. Оцінимо суму довжин всіх цих інтервалів. Для цього введемо позначення: 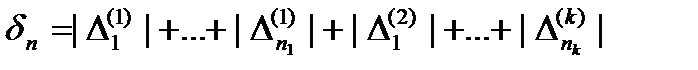
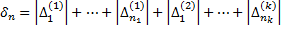 ;
;
 - сума довжин інтервалів, які утворюють множину
- сума довжин інтервалів, які утворюють множину 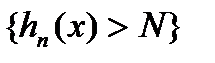 . За умовою ми маємо
. За умовою ми маємо 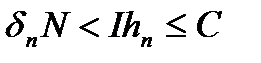 . Звідси
. Звідси  ;
;
Оскільки це вірно для будь-якого  , то ми покладаємо, що повна сума довжин всіх інтервалів, складаючи
, то ми покладаємо, що повна сума довжин всіх інтервалів, складаючи  , не перевищує
, не перевищує  . Так як
. Так як  можна було взяти як завгодно великим, то ми бачимо, що
можна було взяти як завгодно великим, то ми бачимо, що 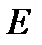 можна покрити скінченною системою інтервалів з загальною довжиною, як завгодно малою. Отже,
можна покрити скінченною системою інтервалів з загальною довжиною, як завгодно малою. Отже, 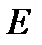 є множиною міри нуль, що й стверджувалося.
є множиною міри нуль, що й стверджувалося.
Взагалі кажучи, будь-яка функція 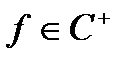 вимірна. Визначим тепер інтеграл від функції
вимірна. Визначим тепер інтеграл від функції 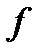 класу
класу  формулою
формулою
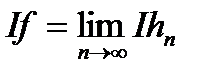 ,
,
де 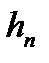 - послідовність східчастих функцій, яка бере участь у визначенні функції
- послідовність східчастих функцій, яка бере участь у визначенні функції 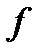 .
.
Оскільки послідовність чисел  монотонна, зростаюча і обмежена, то границя справа існує; але ми повинні ще довести, що вона не залежить від вибору послідовності
монотонна, зростаюча і обмежена, то границя справа існує; але ми повинні ще довести, що вона не залежить від вибору послідовності 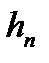 яка визначає функцію
яка визначає функцію  . Для цього ми доведемо наступний, більш узагальнений факт: якщо
. Для цього ми доведемо наступний, більш узагальнений факт: якщо 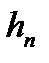 i
i 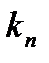 - східчасті функції з обмеженими в сукупності інтегралами і майже скрізь
- східчасті функції з обмеженими в сукупності інтегралами і майже скрізь 
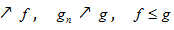 то
то  .
.
Для доведення фіксуємо номер 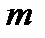 і розглянемо спадну послідовність східчастих функцій
і розглянемо спадну послідовність східчастих функцій 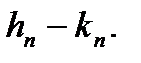 .Її границя
.Її границя 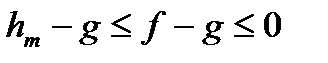 ; але тоді
; але тоді 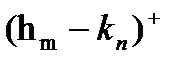
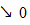 , звідки, за властивістю iv),
, звідки, за властивістю iv),
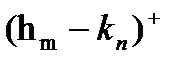
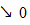 ;
;
але так як  то
то  , спадаючи, прямує до деякої недостатньої границі. Звідси ми робимо висновок, що
, спадаючи, прямує до деякої недостатньої границі. Звідси ми робимо висновок, що 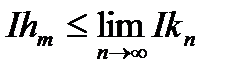 оскільки ця нерівність вірна для будь-якого
оскільки ця нерівність вірна для будь-якого 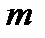 , то, переходячи до границі при
, то, переходячи до границі при  , отримаємо (3), що і вимагалось. Покладаючи
, отримаємо (3), що і вимагалось. Покладаючи 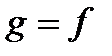 отримаємо
отримаємо 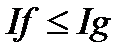 звідки випливає
звідки випливає 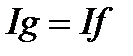 . Таким чином, визначення інтеграла функції
. Таким чином, визначення інтеграла функції 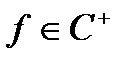 , за формулою (2) однозначне. Якщо ж
, за формулою (2) однозначне. Якщо ж 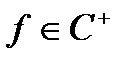 ,
, 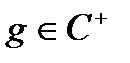 ,
,  то має місце нерівність
то має місце нерівність 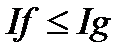 .
.
Взагалі кажучи, будь-яка функція 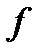 , інтегрована в розумінні Рімана, як границя нижніх сум, співпадає з визначеним нами інтегралом
, інтегрована в розумінні Рімана, як границя нижніх сум, співпадає з визначеним нами інтегралом 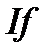 , як границею інтегралів від східчастих функцій
, як границею інтегралів від східчастих функцій 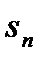 , які відповідають тим же нижнім сумам.
, які відповідають тим же нижнім сумам.
Нове означення інтеграла набагато ширше, ніж означення інтеграла Рімана: наприклад, функція Діріхле 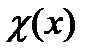 рівна нулеві при ірраціональному
рівна нулеві при ірраціональному  і одиничці при
і одиничці при  раціональному, не була інтегрованою за Ріманом; з нашої ж нової точки зору вона майже скрізь рівна нулеві, а тому інтегрована і має інтеграл рівний нулю. Можна навести і більш складніші приклади, коли інтегрована в новому розумінні функція не інтегрована за Ріманом і не можу бути перетворена в інтегровану за Ріманом змінами на множині міри нуль.
раціональному, не була інтегрованою за Ріманом; з нашої ж нової точки зору вона майже скрізь рівна нулеві, а тому інтегрована і має інтеграл рівний нулю. Можна навести і більш складніші приклади, коли інтегрована в новому розумінні функція не інтегрована за Ріманом і не можу бути перетворена в інтегровану за Ріманом змінами на множині міри нуль.
Здійснюючи граничний перехід, можна перенести деякі властивості інтегралів від східчастих функцій на інтеграли від функцій класу 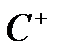 . А саме:
. А саме:
1) Клас 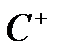 разом з функціями
разом з функціями 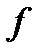 i
i 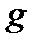 містить
містить 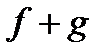 і
і 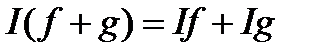 .
.
2) Клас 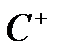 разом з функціями
разом з функціями 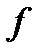 містить її добуток на будь-яке число
містить її добуток на будь-яке число  і
і 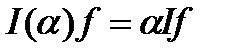 .
.
3) Клас 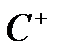 з функціями
з функціями 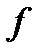 i
i 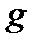 містить
містить 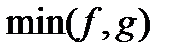 ,
, 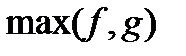 .
.
Зауважимо, що в класі 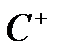 не можна віднімати функції і множити їх на від’ємні числа, оскільки ми весь час повинні мати зростаючі послідовності східчастих функцій.
не можна віднімати функції і множити їх на від’ємні числа, оскільки ми весь час повинні мати зростаючі послідовності східчастих функцій.
Взагалі кажучи, функція  належить класу
належить класу 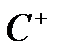 разом з функцією
разом з функцією 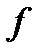 (що не можна сказати про функції
(що не можна сказати про функції  i
i  ).
). 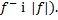 Наступна власти- вість показує, що клас
Наступна власти- вість показує, що клас 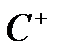 замкнутий відносно граничного переходу за зростаючими послідовностями функцій з обмеженими інтегралами:
замкнутий відносно граничного переходу за зростаючими послідовностями функцій з обмеженими інтегралами:
Теорема 2.3. Якщо 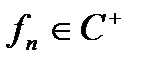

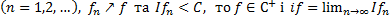
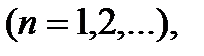
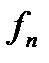
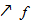 та
та 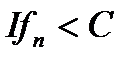 , то
, то 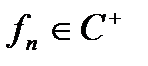 i
i 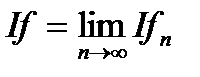 .
.
Доведення. Для кожної із функцій 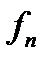 побудуємо визначаючу її зростаючу послідовність східчастих функцій:
побудуємо визначаючу її зростаючу послідовність східчастих функцій:
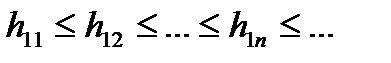 ,
, 
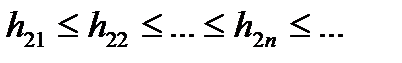 ,
, 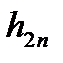
…………………………………………..
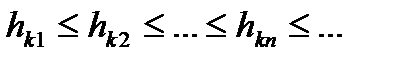 ,
, 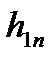
 і т.д.
і т.д.
Далі покладемо  .
. 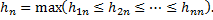 Очевидно, що також східчаста функція і послідовність
Очевидно, що також східчаста функція і послідовність 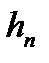
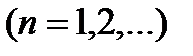 монотонно зростає. Далі,
монотонно зростає. Далі, 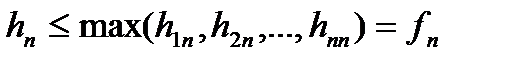 звідки
звідки  . Позначимо через
. Позначимо через 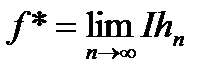 ; згідно означення класу
; згідно означення класу 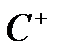 ми маємо
ми маємо 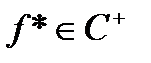 та
та 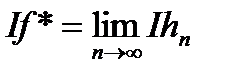 . Але так як
. Але так як 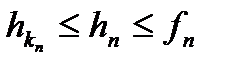 для будь-якого фіксованого
для будь-якого фіксованого 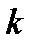 і
і 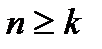 , то переходячи до границі при
, то переходячи до границі при 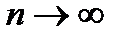 знаходимо
знаходимо 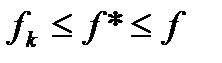 звідки
звідки 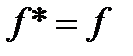 (майже скрізь). Таким чином,
(майже скрізь). Таким чином, 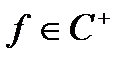 . Потім
. Потім 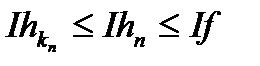 ; так як
; так як 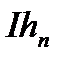
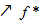 то
то 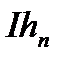
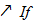 , чим доведення і завершується.
, чим доведення і завершується.
Наслідок. Якщо для ряду 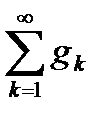 ,
, 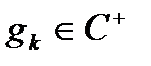 ,
, 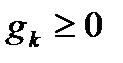 , інтеграли від частинних сум обмежені, так що
, інтеграли від частинних сум обмежені, так що 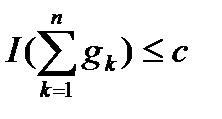 то
то 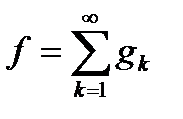 є функцією класу
є функцією класу 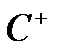 та
та  .
.  Для доведення досить покласти
Для доведення досить покласти 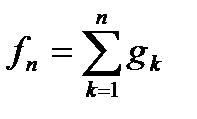 і застосувати теорему 2.3.
і застосувати теорему 2.3.
|
|
|
|
|
Дата добавления: 2015-08-31; Просмотров: 691; Нарушение авторских прав?; Мы поможем в написании вашей работы!