Методика расчета ошибки выборочной средней и выборочной доли

Ошибка выборочной совокупности и их классификация.

Способы отбора выборочной совокупности.

Способы отбора единиц,применяемые в практике выборочного метода исследования, определяются правилами формирования выборочной совокупности,в зависимости от которых выборка может быть:

1) собственно-случайная - состоит в том,что выборочная совокупность получается в результате случайного отбора отдельных единиц из генеральной совокупности. Кол-во единиц определяется исходя из принятой доли выборки. Примерами такой выборки могут служить розыгрыш "Спортлото",жеребьевка и т.д.

2) механическая -состоит в том,что отбор единиц в выборку производится из генеральной совокупности, упорядоченной по признаку,не подлежащему изучению. Затем с определенным шагом выбирается необходимое число ед.,обратное величине заданной доли выборки. Так,при 5% выборке механически й отбор всегда бесповторный.

3) типическая - состоит в том, что генеральная совокупность вначале расчленяется на однородные типические группы,затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор ед. в выборочную совокупность. Отбор ед. может быть пропорциональным удельному весу каждой группы или непропорциональным. Типическая выборка применяется при изучении сложных статистических совокупностей. Например, при выборочном обследовании производительности труда работников,состоящих из отдельных групп квалификации. Типическая выборка дает более точные результаты по сравнению с другими способами отбора ед., что обеспечивается расчленением генеральной совокупности на качественно однородные группы и представительством в выборке (репрезентативностью) каждой типологической группы.

4) серийная(гнездовая) -состоит в том,что из генеральной совокупности отбираются не отдельные ед.,а целые их серии(гнезда), причем внутри каждой серии обследуются все без исключения ед. Серии могут быть как равновеликие, так и неравновеликие по численности.

5) комбинированная - заключается в том,что одновременно используются (комбинируются) несколько предыдущих способов отбора. Например,серийный отбор сочетается с собственно-случайным.

Объективно возникающее расхождение между характеристиками выборки и генеральной совокупностью составляет ошибку выборки, которая зависит от ряда факторов:степени вариации изучаемого признака,численности выборки,методов отбора ед. в выборочную совокупность,принятого уровня достоверности результата исследования.

Возможные расхождения между характеристикой выборочной и генеральной 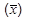совокупности измеряются средней ошибкой выборки µ.В математической статистике доказывается,что величина средней ошибки выборки определяется по формуле:

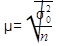
n -численность ед.выборки

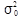-дисперсия генеральной совокупности

При повторном отборе средняя ошибка выборочной доли рассчитывается по формуле

При бесповторном отборе она рассчитывается по формуле:

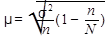
где N — численность генеральной совокупности.

Предельная ошибка выборки находится по формуле:

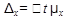
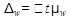
При организации выборочного наблюдения следует иметь ввиду, что размер ошибки выборки прежде всего зависит от численности выборочной совокупности n. Из формулы для ошибки выборки μвидно, что средняя ошибка выборки обратно пропорциональна 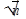т.е. при увеличении численности выборки,например,в 9 раз,ошибка выборки уменьшается только в 3 раза.

Определение необходимой численности выборки основывается на формулах для предельной ошибки выборки Δ_х и Δ_w.Необходимый объем выборки можно получить путем решения этих равенств относительно n. Например,необходимая численность выборки при определении средней величины количественного признака х выразится формулой

в случае повторного отбора. Для бесповторного отбора имеет место формула

Необходимая численность выборки при определении доли альтернативного признака --- в генеральной совокупности рассчитывается по формуле

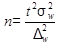
для повторного отбора и по формуле

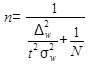
для бесповторного отбора.

Дата добавления: 2015-08-31