Статистический анализ динамики средней заработной платы

На практике большое значение имеет анализ динамики средней заработной платы по совокупности предприятий объединения, концерна, отрасли и т.п., либо по совокупности цехов предприятия, либо совокупности отдельных категорий работников предприятия и т.д.

В этих случаях для анализа динамики зарплаты рассчитывается индекс переменного состава по формуле

: , (5.19)

где З₀,З₁ – средняя заработная плата по элементам изучаемой совокупности соответственно в базисном и отчетном периоде;

Т₀,Т₁ – среднесписочная численность работников по элементам изучаемой совокупности соответственно в базисном и отчетном периоде;

- фонд заработной платы по элементам изучаемой совокупности соответственно в базисном и отчетном периодах.

Далее проводится факторный анализ и даётся количественная оценка влияния отдельных факторов на динамику средней зарплаты в целом по изучаемой совокупности.

Во-первых, оценивается влияние изменения уровня оплаты труда в отдельных структурных звеньях изучаемой совокупности на изменение уровня оплаты труда в целом в среднем по совокупности. Для этих целей рассчитывают индекс фиксированного (постоянного) состава:

, (5.20)

который чаше используют в виде:

. (5.21)

Во-вторых, дается оценка влияния изменений в структуре работников, т.е. в распределении работников с различным уровнем оплаты труда с помощью индекса структурных сдвигов:

. (5.22)

Учитывая, что между индексами переменного, постоянного состава и структурных сдвигов существует взаимосвязь:

, (5.23)

на практике индекс структурных сдвигов чаще определяют как отношение

. (5.24)

Например, необходимо определить изменение средней заработной платы рабочих предприятия и выявить за счет каких факторов сложилось это изменение (цифры условные).

Определим, как изменился уровень средней заработной платы в целом по категории «рабочие» с помощью индекса переменного состава:

.

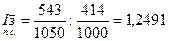Таблица 5.2 – Заработная плата рабочих предприятия

Группы	Среднесписочная численность, чел.	Фонд зарплаты, млн.руб.	Средн. зарплата, тыс. руб.		Доля рабочих, %
рабочих	Базисный период	Отчётн. период	Базисный период	Отчётн. период	Базисный период	Отчётн. период	З0Т1	Базисный период	Отчётн. период
	Т0	Т1	Ф0	Ф1	З0	З1	млн. р.
Основные рабочие							427,5	80,0	90,5
Вспомог. рабочие							27,0	20,0	9,5
Всего	1 000	1 050					454,5	100,0	100,0

Рассмотрим факторные индексы:

- индекс постоянного (фиксированного) состава:

;

- индекс структурных сдвигов:

.

Следовательно, в отчётном периоде по сравнению с базисным уровень средней зарплаты рабочих на исследуемом предприятии повысился на 24,91%. Этот рост был вызван двумя причинами:

- за счет изменения непосредственно оплаты труда (из табл. 5.2 видно, что средняя зарплата увеличилась и у основных, и у вспомогательных рабочих) уровень средней зарплаты по категории «рабочие» повысился на 19,47%;

- за счёт увеличения доли основных рабочих (это доказывают две последние графы табл. 5.2), которые имеют более высокую зарплату, чем вспомогательные, средняя заработная плата по исследуемой совокупности увеличилась на 4,55%.

Дата добавления: 2015-08-31