Закон Гука для тонкого стержня

Для тонкого растяжимого стержня закон Гука имеет вид:

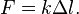
Здесь 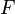— сила, которой растягивают (сжимают) стержень, — абсолютное удлинение (сжатие) стержня, а 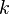— коэффициент упругости (или жёсткости).

Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения 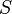и длины 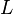) явно, записав коэффициент упругости как

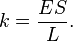
Величина 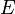называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала.

Если ввести относительное удлинение

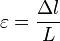
и нормальное напряжение в поперечном сечении

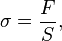
то закон Гука для относительных величин запишется как

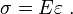
В такой форме он справедлив для любых малых объёмов материала.

Также при расчёте прямых стержней применяют запись закона Гука в относительной форме

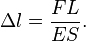
Обобщённый закон Гука

В общем случае напряжения и деформации описываются тензорами второго ранга в трёхмерном пространстве (имеют по 9 компонент). Связывающий их тензор упругих постоянных является тензором четвёртого ранга 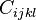и содержит 81 коэффициент. Вследствие симметрии тензора 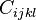, а также тензоров напряжений идеформаций, независимыми являются только 21 постоянная. Закон Гука выглядит следующим образом:

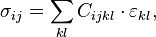
где 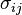— тензор напряжений, 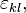— тензор деформаций. Для изотропного материала тензор 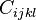содержит только два независимых коэффициента.

Благодаря симметрии тензоров напряжения и деформации, закон Гука может быть представлен в матричной форме.

Для линейно упругого изотропного тела:

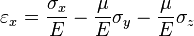
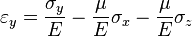
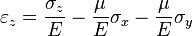
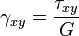
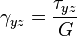
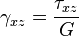
где 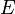— модуль Юнга, 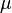— коэффициент Пуассона, 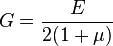— модуль сдвига.

1. УРАВНЕНИЯ ДВИЖЕНИЯ УПРУГОЙ СРЕДЫ.

1. ОБЬЕМНЫЕ УПРУГИЕ ВОЛНЫ.

1. ВЛИЯНИЕ ГРАНИЦ НА РАСПРАСТРАНЕНИЕ УПРУГИХ ВОЛН.

1. ГОДОГРАФЫ.

Дата добавления: 2015-08-31