Графическое определение аномалии силы тяжести двухмерных тел с помощью палетки Гамбурцева

ОБРАТНАЯ ЗАДАЧА ТЕОРИИ ПОТЕНЦИАЛА И МЕТОДЫ ЕЕ РЕШЕНИЯ.

Нахождение аномалий силы тяжести и вторых производных потенциала от тел известной формы, глубины залегания, размера и плотности носит название прямой задачи гравиразведки. Определение местоположения, формы, глубины залегания, размеров и плотности тел по известным аномалиям 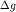или вторых производных потенциала силы тяжести называется обратной задачей гравиразведки.

В результате гравиразведки рассчитываются аномалии силы тяжести, обусловленные теми или иными плотностными неоднородностями, а влияние притяжения всей Земли и окружающего рельефа исключается вычитанием нормального поля и введением редукций (см. 1.2.3). Поэтому в математической теории гравиразведкирасcчитываются аномалии от тел простых форм: шара, горизонтального цилиндра, вертикального уступа, вертикального цилиндра и т.д. без учета притяжения всей Землей.

Нахождение аномалий силы тяжести и вторых производных потенциала от тел известной формы, глубины залегания, размера и плотности носит название прямой задачи гравиразведки. Определение местоположения, формы, глубины залегания, размеров и плотности тел по известным аномалиям 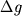или вторых производных потенциала силы тяжести называется обратной задачей гравиразведки.

Обратная задача над шаром.

Обратная задача. Из (1.11) максимум 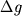над центром шара (x =0) равен .

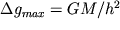Для точки, удаленной от максимума на расстояние x_1/2, имеющей 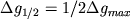, можно записать следующее уравнение:

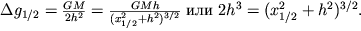
Решив последнее уравнение, получим формулу для определения глубины залегания центра шара h=1,3x_1/2. Зная 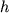, легко найти избыточную массу (): .

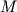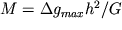Так как 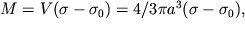то, зная избыточную плотность 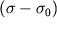, можно рассчитать объем (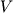) и радиус шара (). Так, радиус равен:

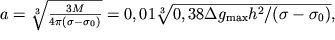
где 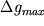- в миллигалах, 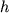- в метрах, 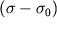- в тоннах / куб. метр (г/см³).

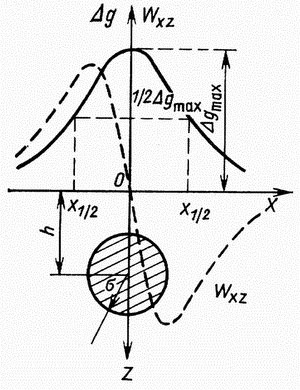
Рис.1.3 Гравитационное поле шара

Обратная задача над горизонтальным бесконечно длинным круговым цилиндром.

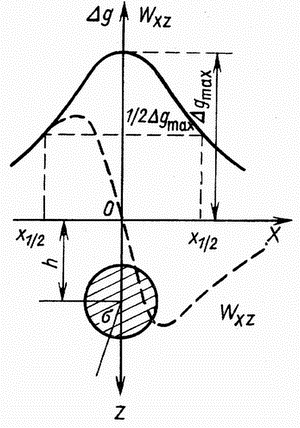
Рис.1.4 Гравитационное поле бесконечно длинного кругового горизонтального цилиндра

. Обратная задача. Из (1.10 и 1.12) можно при х =0 получить 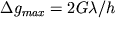. Отсюда

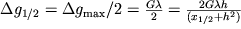
и 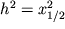, , 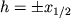т.е. глубина залегания цилиндра равна расстоянию от точки максимума 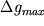до точки, где .

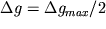Определив 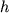и зная избыточную плотность, можно рассчитать

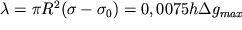
и радиус цилиндра:

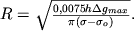
Зная 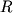, можно получить глубины залегания верхней h_в=h-R и нижней h_н=h+R кромок цилиндра. Нетрудно вычислить выражение и для .

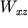Обратная задача над вертикальным уступом (сбросом).

Обратная задача. Из (1.14) можно определить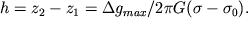

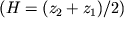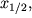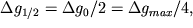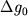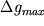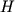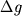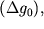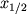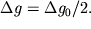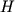В теории гравиразведки доказано, что примерная глубина расположения середины высоты уступа равна т.е. абсциссе точки, в которой где - аномалия над уступом, а - полная аномалия. Практически для определения на кривой находится местоположение сброса и в масштабе профиля рассчитывается - расстояние от сброса до точки, в которой Зная и 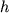, легко определить глубины до приподнятого 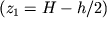и опущенного 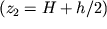крыла.

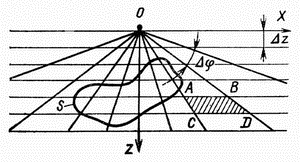
Рис.1.6 Палетка Гамбурцева для вычисления притяжения двухмерных тел

Обратная задача. Используя (1.16) с помощью палетки Гамбурцева, можно выяснить форму и положение сечения возмущающего двухмерного аномалосоздающего объекта. Для этого надо знать избыточную плотность 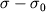, оценить аналитическим способом положение ее центра и для нескольких точек графика 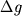построить возможные сечения возмущающего тела. Среднее из них характеризует примерное сечение тела.

Дата добавления: 2015-08-31