Доказательство

Пусть в конечномерном линейном пространстве L, размерности n, зафиксирован базис и задано линейное преобразование А.

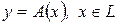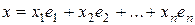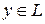Пусть , где , , тогда, поскольку , то , .

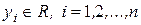С другой стороны, в силу линейности преобразования А,

.

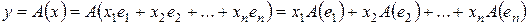Так как , то они так же могут быть разложены по базису .

Пусть ,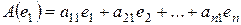

,

.

Тогда, подставляя эти разложения в полученное выше представление для вектора у, получаем:

Выделяя коэффициенты при базисных векторах , приходим к равенству:

В силу единственности разложения вектора у по базису приходим к системе:

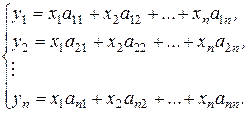
Вводя матрицы ,

систему можно представить в виде матричного уравнения:

.

Данное уравнение позволяет при известных матрице А и столбце координат Х вектора х найти столбец координат У вектора у. Единственность следует из единственности разложения образов базисных векторов и исходного вектора х по базису.

Определение 3. Матрица , столбцы которой – координаты образов базисных векторов при преобразовании А, называется матрицей линейного преобразования в базисе .

Замечание. В тоже время, наоборот, в конечномерном линейном пространстве L, размерности n, с фиксированным базисом, каждой квадратной матрице 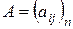можно поставить в соответствие преобразование по правилу: если X - столбец координат вектора х в выбранном базисе, то - столбец координат вектора у в этом базисе, где .

Более того, данное преобразование будет линейным. Действительно.

1) Если столбец координат вектора х – Х, столбец координат вектора у – У, то столбец координат вектора 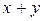- . Столбец координат вектора , вектора , вектора , вектора . Так как 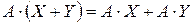, то свойство выполняется.

2) Если столбец координат вектора х - Х, то столбец координат вектора . Столбец координат вектора , вектора , вектора . Так как 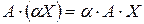, то свойство выполняется.

Таким образом, в конечномерном линейном пространстве L, размерности n, с фиксированным базисом существует взаимно однозначное соответствие между линейными преобразованиями и квадратными матрицами размерности n.

Как уже было отмечено выше, в конечномерном линейном пространстве вид матрицы линейного преобразования зависит от выбора базиса.

Выведем формулы для связи матриц линейного преобразования в двух базисах одного и того же конечномерного линейного пространства.

Пусть задано линейное пространство L размерности n, в котором заданы два базиса и 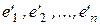, причем, известна матрица Т перехода от базиса к базису .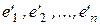

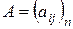Пусть линейное преобразование A в базисе имеет матрицу , а в базисе 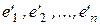- матрицу .

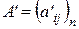Пусть , где 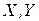– столбцы координат векторов х, у в базисе ; - столбцы координат векторов х, у в базисе .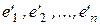

В базисе

.

Учитывая связь координат векторов х и у в базисах и :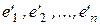

,

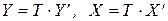получаем, что .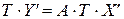

Так как матрица перехода Т – невырожденная, то у неё существует обратная матрица . Умножая обе части получившегося равенства слева на , имеем:

,

,

.

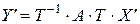С дугой стороны, в базисе 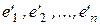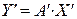, следовательно,

.

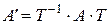Нетрудно заметить (проделайте соответствующие выкладки самостоятельно), что

.

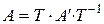Теорема 2. Величина определителя матрицы линейного преобразования в конечномерном линейном пространстве не зависит от выбора базиса, т.е. является инвариантной величиной относительно базиса.

Доказательство. Пусть в конечномерном линейном пространстве L размерности n задано некоторое линейное преобразование A.

Зафиксируем в этом пространстве произвольным образом два базиса и .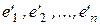

Пусть А и 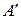- матрицы линейного преобразования А в базисах и 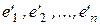, соответственно.

По доказанному выше, матрицы линейного преобразования в этом случае связаны по правилу: 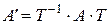, где Т – матрица перехода от базиса к базису 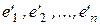. Анализируя величину определителя матрицы 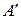, получаем:

.

В силу произвольности выбора базисов результат будет справедлив для любых базисов, следовательно, величина матрицы линейного преобразования не зависит от базиса. Теорема доказана.

Нетрудно заметить, что для любого линейного преобразования А в любом линейном пространстве L 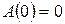, так как .

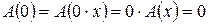Определение 4. Линейное преобразование А называется невырожденным, если 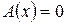, только при 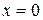. В противном случае, если найдется ненулевой элемент , такой что 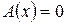, линейное преобразование называется вырожденным.

Теорема 3. В конечномерном линейном пространстве L линейное преобразование A является невырожденным тогда и только тогда, когда матрица линейного преобразования является невырожденной.

Доказательство. Так как величина определителя матрицы линейного преобразования в конечномерном линейном пространстве не зависит от выбора базиса, то достаточно доказать справедливость этого утверждения для любого базиса.

Пусть и - некоторый фиксированный базис.

Пусть 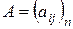- матрица линейного преобразования А в базисе , Х – столбец координат вектора х в базисе .

Очевидно, что 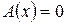, только при 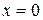, тогда и только тогда, когда получившаяся система имеет только нулевое решение, а это возможно лишь тогда и только тогда, когда определитель системы равен нулю. Так как определитель системы – определитель матрицы линейного преобразования, то теорема доказана.

Следствие. В конечномерном линейном пространстве L линейное преобразование A является вырожденным тогда и только тогда, когда матрица линейного преобразования является вырожденной.

Доказательство. Справедливость этого утверждения следует из того, что система, полученная при доказательстве теоремы 3 имеет нетривиальное (ненулевое) решение тогда и только тогда, когда определитель, составленный из коэффициентов при неизвестных, равен нулю.

Определение 5. Линейное преобразование А называется тождественным, если .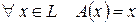

Очевидно, что в конечномерном линейном пространстве L, размерности n, в любом базисе соответствует единичная матрица порядка n.

Действительно.

,

,

.

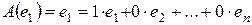Следовательно, матрица линейного преобразования А в данном базисе имеет вид:

.

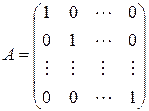Дата добавления: 2015-08-31