Зависимость производительности от числа операций на обработку сообщения. 1 страница

Зависимость производительности от быстродействия процессора

Оценим производительность системы при увеличении быстродействия процессора в 2 раза: S = 3100 тыс.оп./с. Из формулы (2) получается:

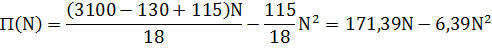
Результаты сравнения с первоначальным примером показаны на рисунке 4.

Очевидно, что при увеличении быстродействия при неизменности остальных параметров, производительность системы заметно возрастает. Уже у двухпроцессорной усовершенствованной системы ее производительность достигнет уровня, которого не было бы при N_опт в старой системе. Следовательно, можно сделать вывод, что система очень чувствительна к изменению данной характеристики.

	П(N)
N	S=1550	S=3100
	78,88888889
		317,22
	198,3333333	456,66
	238,8888889	583,32
	266,6666667	697,2
	281,6666667	798,3
	283,8888889	886,62
	273,3333333	962,16
		1024,92
	213,8888889	1074,9
		1112,1		Рис. 4. Производительность СОС для двух значений быстродействия процессора
	103,3333333	1136,52

Рассмотрим влияние изменения числа операций на обработку сообщения на производительность системы. Пусть Т = 36 тыс.оп./сообщ. Тогда из формулы (1) следует:

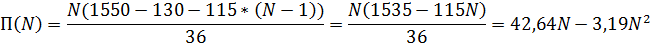
Результаты сравнения с первоначальным примером показаны на рисунке 5.

Получается, что при шестипроцессорной системе с числом затрачиваемых операций на сообщение равным 36 тыс., производительность будет примерно в 2 раза ниже исходной. Так, для шестипроцессорной СОС, производительность снизится с 291,67 сообщ./с. до 141 сообщ./с.

	П(N)
N	T=18	T=36
	78,88888889	39,45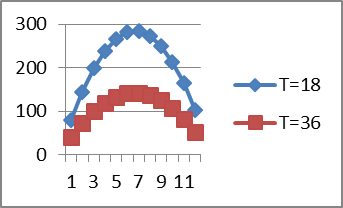
		72,52
	198,3333333	99,21
	238,8888889	119,52
	266,6666667	133,45
	281,6666667
	283,8888889	142,17
	273,3333333	136,96
		125,37
	213,8888889	107,4
		83,05	Рис. 5. Производительность СОС для двух значений числа операций обработки сообщения
	103,3333333	52,32

3.1 Чувствительность СОС к числу процессоров

Если имеется функция П(a,b,…,z), зависящая от нескольких параметров, ее чувствительность к одному из них, например z, в данной точке (a_0, b_{0, …} z₀) можно определить вычислением производной функции П по z в точке (a_0, b_{0, …} z₀):

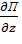(a_0, b_{0, …} z₀).

В случае СОС по формуле (1) можно получить

N(S, P, M, T) = N[S – P – M(N – 1)]/T = N(S – P)/T – MN(N - 1)/T (6)

Поэтому частная производная функция П по М имеет вид

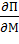(6, 1550, 130, М, 18) = 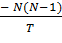_{N = 6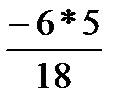} = ≈ -1

^T=18

Полученное значение представляет собой тангенс угла наклона характеристики чувствительности (рис.6, 7, 8, 9).

Из этих графиков видно, что производительность шестипроцессорной системы:

- более чувствительна к изменению коэффициента межпроцессорных накладных расходов (рис.6) и понижается с увеличением этого коэффициента;

- более чувствительна к изменению быстродействия процессора (рис. 7) и повышается с его увеличением;

- более чувствительна к изменению внутрипроцессорных накладных расходов (рис. 8) и понижается с его увеличением;

- более чувствительна к изменению числа операций на обработку сообщения (рис.9) и понижается с увеличением этого коэффициента.

3.1.1Чувствительность СОС к изменению параметра М

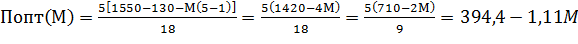
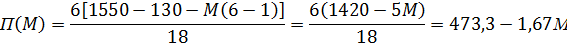
В рассматриваемом случае шестипроцессорной СОС любое увеличение коэффициента межпроцессорных накладных расходов на 30 единиц приведет к уменьшению производительности СОС на 50 сообщ./с (рис. 6).

Из графика видно, что чем меньше число процессоров, тем меньше будут межпроцессорные расходы, и как следствие, тем больше будет производительность системы.

M	Попт(М) (N=6)	П(М) (N=5)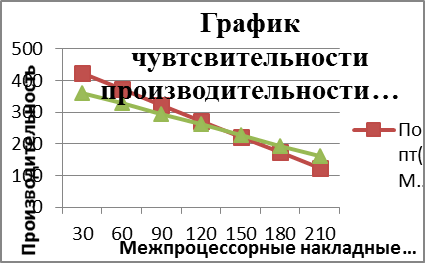
	423,2	361,1
	373,1	327,8
		294,5
	272,9	261,2
	222,8	227,9
	172,7	194,6		Рис. 6. График чувствительности производительности системы к M при N=5 и N=6
	122,6	161,3

3.1.2 Зависимость производительности от быстродействия процессора

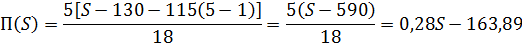
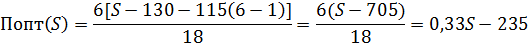
S	Попт(S) (N=6)	П(S) (N=5)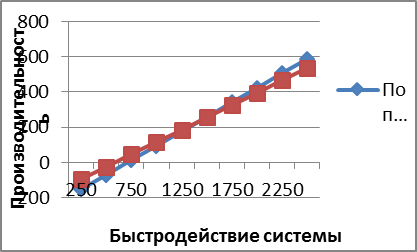
	-152,5	-93,9
	-70	-23,9
	12,5	46,1
		116,1
	177,5	186,1
		256,1
	342,5	326,1
		396,1
	507,5	466,1
		536,1		Рис.7. График чувствительности производительности системы к S при N=5 и N=6

Отсюда видно, что при увеличении быстродействия процессора производительность СОС так же увеличивается.

3.1.3 Чувствительность СОС к изменению параметра P

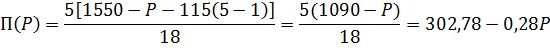
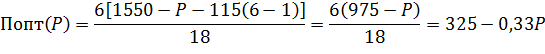
P	Попт(P) (N=6)	П(P) (N=5)
		274,78
		246,78
		218,78
		190,78
		162,78
		134,78
		106,78
		78,78
		50,78
	-5	22,78	Рис.8. График чувствительности производительности системы к S при N=5 и N=6

Очевидно, что при увеличении внутрипроцессорных накладных расходов производительность системы будет значительно уменьшаться. Чем меньшее число процессоров, тем меньше будет между ними междупроцессорных расходов, что приведет к значительному росту производительности СОС.

3.1.4 Чувствительность СОС к изменению параметра T

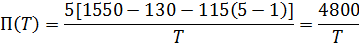
T	Попт(T) (N=6)	П(T) (N=5)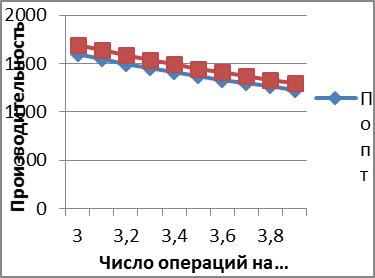
3,1	1548,387097	1635,483871
3,2		1584,375
3,3	1454,545455	1536,363636
3,4	1411,764706	1491,176471
3,5	1371,428571	1448,571429
3,6	1333,333333	1408,333333
3,7	1297,297297	1370,27027
3,8	1263,157895	1334,210526
3,9	1230,769231
		Рис.9. График чувствительности производительности системы к T при N=5 и N=6

3.2 Перекрестные зависимости

Для полного анализа системы необходимо рассмотреть и перекрестные зависимости – зависимости параметров системы от остальных параметров.

3.2.1 Зависимость межпроцессорных накладных расходов от параметров системы

Межпроцессорные накладные расходы рассчитываются по следующей формуле:

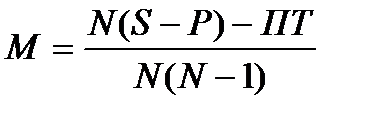(7)

Зависимость коэффициента М от внутрипроцессорных накладных расходов Р

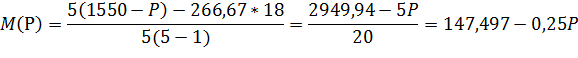
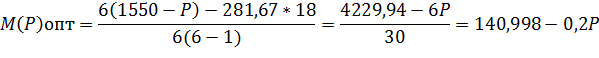
Получается, что в трехпроцессорной системе, межпроцессорные накладные расходы менее устойчивы к изменению внутрипроцессорных накладных расходов. Это можно увидеть на рисунке 10.

P	M(P) N = 5	M(P) N = 6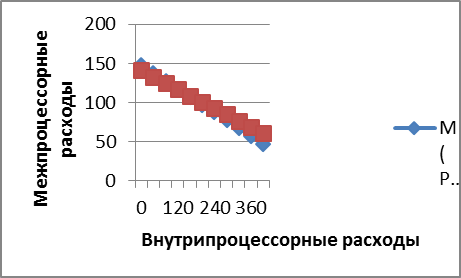
	147,497	140,998
	137,497	132,998
	127,497	124,998
	117,497	116,998
	107,497	108,998
	97,497	100,998
	87,497	92,998
	77,497	84,998
	67,497	76,998
	57,497	68,998
	47,497	60,998
		Рис.10. График чувствительности межпроцессорных накладных расходов системы к P при N=5 и N=6

При увеличении внутрипроцессорных расходов на 40 тыс. операций в секунду межпроцессорные накладные расходы сокращаются, в среднем на 8-10 тыс. операций в секунду. Это происходит потому, что при увеличении внутрипроцессорных расходов каждый процессор начинает лучше работать, и как следствие, требуется меньше затрат на организацию слаженной работы между процессорами.

Зависимость коэффициента М от быстродействия процессора S

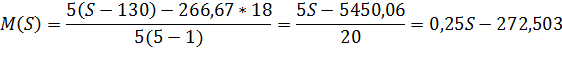
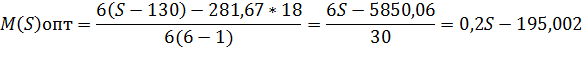
В системе с шестью процессорами, параметр М менее чувствителен к изменению быстродействия процессора (рис.11). Не зависимо от числа процессоров, при увеличении быстродействия процессора, межпроцессорные накладные расходы так же увеличиваются.

P	M(S) N = 5	M(S) N = 6
	-234,503	-165,002
	-197,003	-135,002
	-159,503	-105,002
	-122,003	-75,002
	-84,503	-45,002
	-47,003	-15,002
	-9,503	14,998
	27,997	44,998
	65,497	74,998
	102,997	104,998
	140,497	134,998
		Рис.11. График чувствительности межпроцессорных накладных расходов системы к S при N=5и N=6

Дата добавления: 2015-08-31