Составление структурной схемы САУ

4.1. Структурная схема механической части:

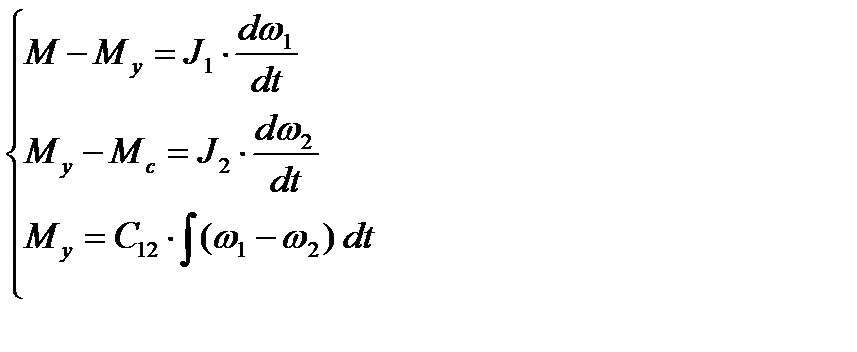
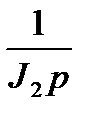
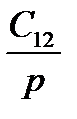
М_д

М_у

М_с

w₂

-

-

-

W₁(p)

W₂(p)

W₃(p)

4.2. Структурная схема двигателя постоянного тока

Структурная схема электродвигателя без учета электромагнитной инерции:

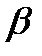
w₀(р)

w₁(р)  

М(р)

-

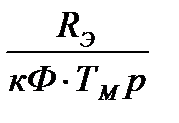
w₁(р)  

-М_с(р)

U_Я(p)

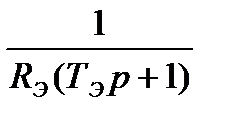
М(р)

I_я(р)

Структурная схема ДПТ с НВ:

4.3. Структурная схема тиристорного преобразователя:

U_У(p)

E_d(p)

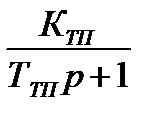
4.4. Структурная схема датчиков цепей обратных связей:

Обратная связь по скорости:

-U_Осi(p)

U_РС(p)

U_ЗТ(p)

I_ДВ(p)

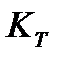
Обратная связь по току:

-U_ОСw(p)

U_З(p)

U_ЗС(p)

w_ДВ(p)

4.5. Структурная схема регулятора скорости:

К_РС

U_З(p)

-U_ОСw(p)

U_ЗС(p)

U_РС(p)

4.6. Структурная схема регулятора тока:

U_РС(p)

-U_ОСi(p)

U_ЗТ(p)

Uу(p)

4.7. Структурная схема (полная) САУ.

Структурная схема САУ с подчиненным регулированием без учета упругости механической передачи приведена на рисунке 4.1.

ω₁

M_c

К_рс

К_с

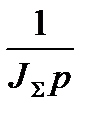
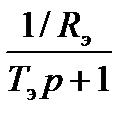
К_т

кФ

кФ

U_З

Рисунок 4.2 – Структурная схема САУ с подчиненным регулированием без учета упругости механической передачи

Структурная схема системы автоматического управления с подчиненным регулированием с учетом упругости механической передачи приведена на рисунке 4.3.

ω₂

M_c

К_рс

К_с

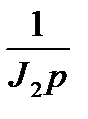
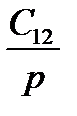
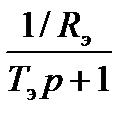
К_т

кФ

кФ

U_З

Рисунок 4.3 – Структурная схема САУ с подчиненным регулированием с учетом упругости механической передачи

5. ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ САУ ПОУПРАВЛЯЮЩЕМУ И ВОЗМУЩАЮЩЕМУ ВОЗДЕЙСТВИЯМ

5.1. Вывод передаточной функции САУ по управляющему воздействию:

ω₂

К_рс

К_с

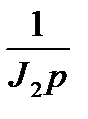
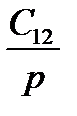
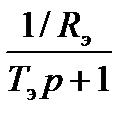
К_т

кФ

кФ

U_З

Мс=0.

Преобразуем схему, пренебрегая обратной связью кФ:

ω₂

W_рс

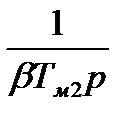
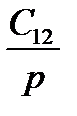
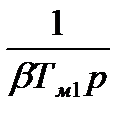
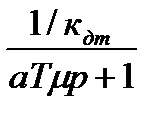
кФ

К_дс

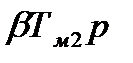
U_З

Определим постоянные времени:

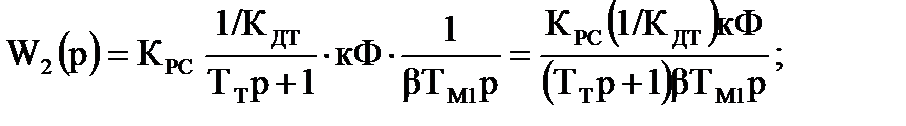
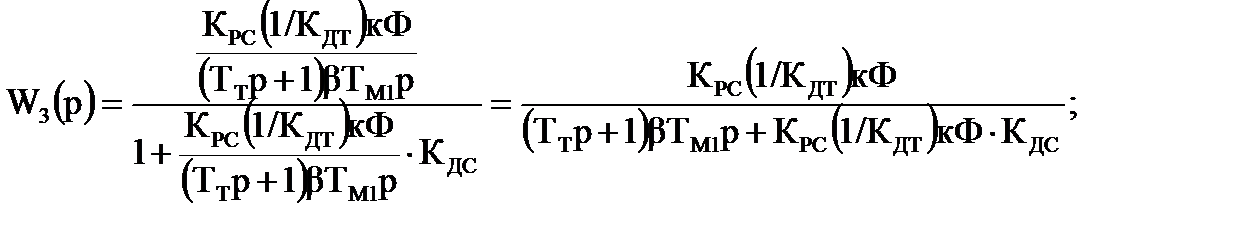
_Wpс(р)  

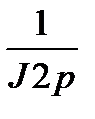
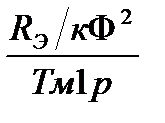
К_с

5.2 Вывод передаточной функции САУ по возмущающему воздействию

ω₂

M_c

К_рс

К_с

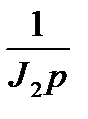
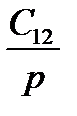
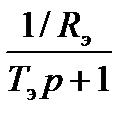
К_т

кФ

кФ

U_З

Преобразуем схему:

_Wpт(р)

К_рс

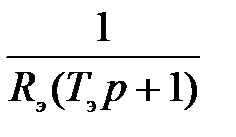
Кдт

кф

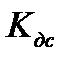
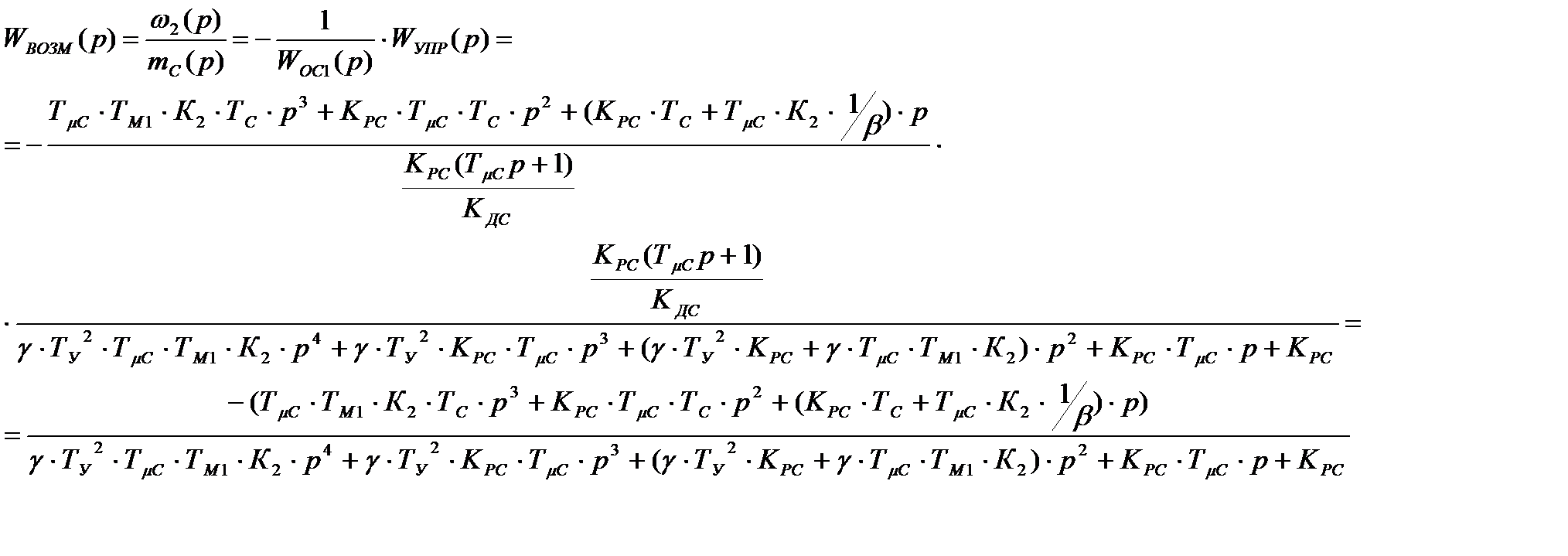
6. ИССЛЕДОВАНИЕ САУ НА УСТОЙЧИВОСТЬ

6.1. Алгебраические критерии устойчивости

Устойчивостью называют свойство системы возвращаться в исходный или принимать новый установившийся режим после всякого выхода из него в результате какого-либо воздействия.

Система устойчива, если ее выходная величина остается ограниченной в условиях действия на систему ограниченных по величине возмущений.

Критерий устойчивости Рауса – Гурвица

Запишем характеристическое уравнение нашей системы: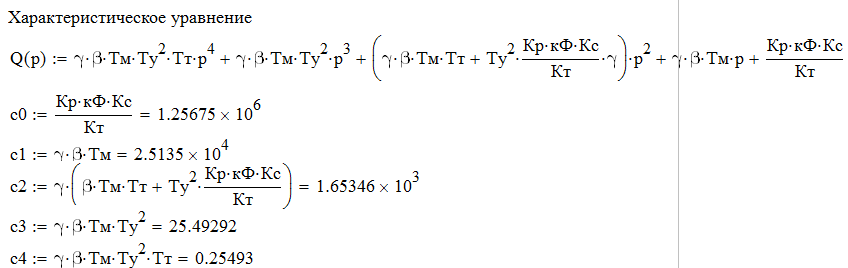

Так как определитель Гурвица больше нуля, то система устойчива.

Корневой метод

Условие устойчивости: все корни характеристического уравнения Q(p) должны лежать слева от мнимой оси.

Запишем характеристическое уравнение системы:

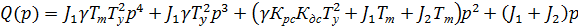
Действительные части корней – отрицательные, поэтому делаем вывод, что система устойчива и дополнительной коррекции не требует.

6.2. Частотные критерии устойчивости

Критерий устойчивости Михайлова.

Критерий Михайлова формируется так: система устойчива, если годограф Q(jw), начинаясь на действительной положительной полуоси, огибает против часовой стрелки начало координат, проходя последовательно n квадрантов, где n – порядок системы.

Запишем характеристическое уравнение системы:

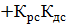
Заменим р на jω:

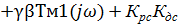
Выделим мнимую и действительную часть

Построим годограф Михайлова с помощью прикладной программы MathCad:

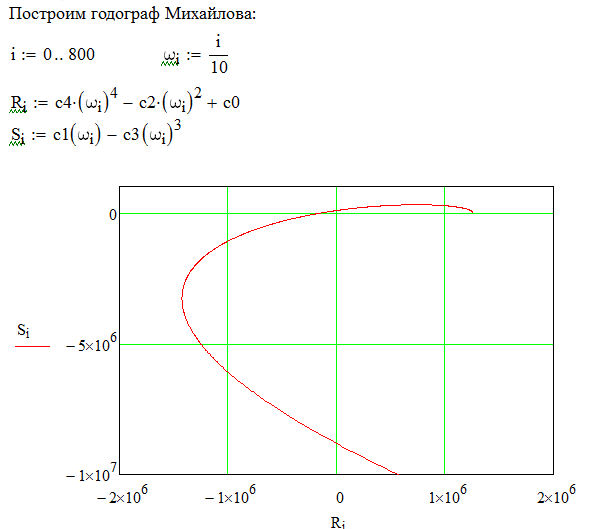
Рисунок 6.1 – Годограф Михайлова

Т.к. годограф последовательно проходит через четыре квадранта, огибая начало координат против часовой стрелки, окончательно можно сделать вывод, что система устойчива.

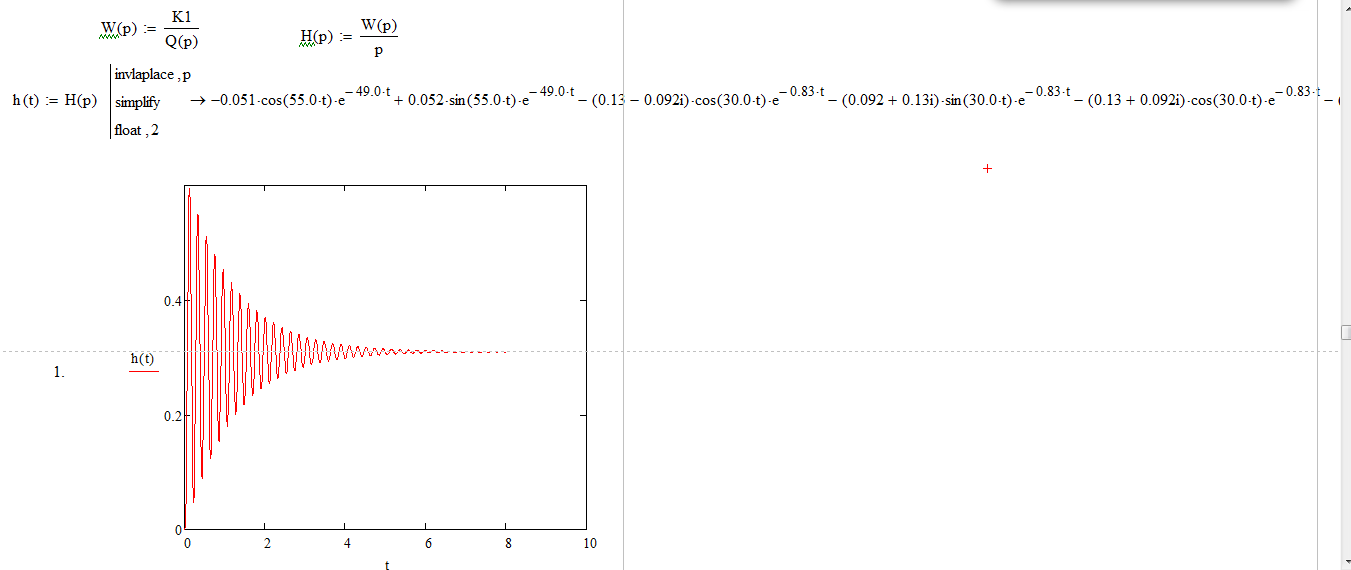Построим график переходных процессов.

Рисунок 6.2 – График переходного процесса

7. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ КАЧЕСТВА САУ

7.1. Определение показателей качества САУ методами теории автоматического управления:

Характеристический полином:

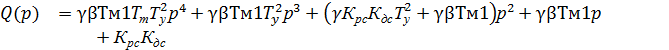
Корни характеристического уравнения:

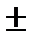-083246 30.17189j

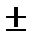54,71524

Берем корни лежащие ближе к мнимой оси.

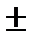-083246 30.17189j

α= -0.83246

β= 30,17189j

Показатели качества регулирования:

1.Запас устойчивости:

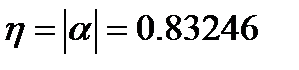
2. Время регулирования:

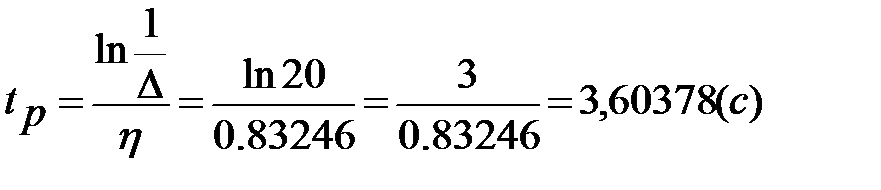
где Δ – ошибка регулирования (Δ = 5%)

3. Колебательность

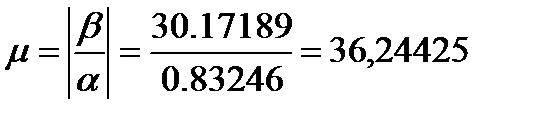
4. Перерегулирование

5. Демфирование

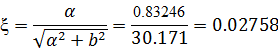
7.2. Сравнительный анализ показателей качества САУ с требуемыми по технологии

Параметры системы, полученные в результате расчета в отношении соответствия требованиям технологического процесса нельзя считать удовлетворительными т.к. колебательность, перерегулирование, время регулирования системы слишком велики. Исходя из этого делаем вывод, что нужна оптимизация САУ.

8. МОДЕЛИРОВАНИЕ САУ И ОПТИМИЗАЦИЯ

8.1 Математическая модель САУ с учетом упругости механической передачи.

Построим модель для симуляции системы в пакете Simulink прикладной программы Matlab.

Рисунок 8.2 – График переходного процесса скорости механизма и момента на валу

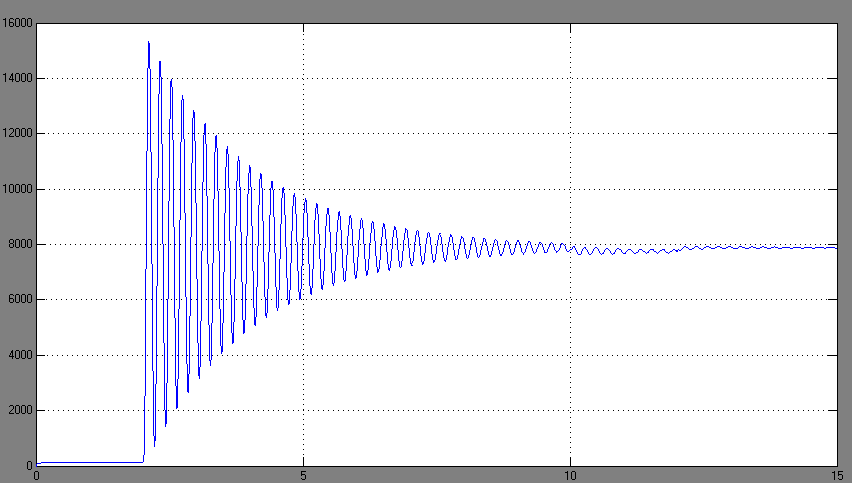
Рисунок 8.3 – График переходного процесса тока якоря

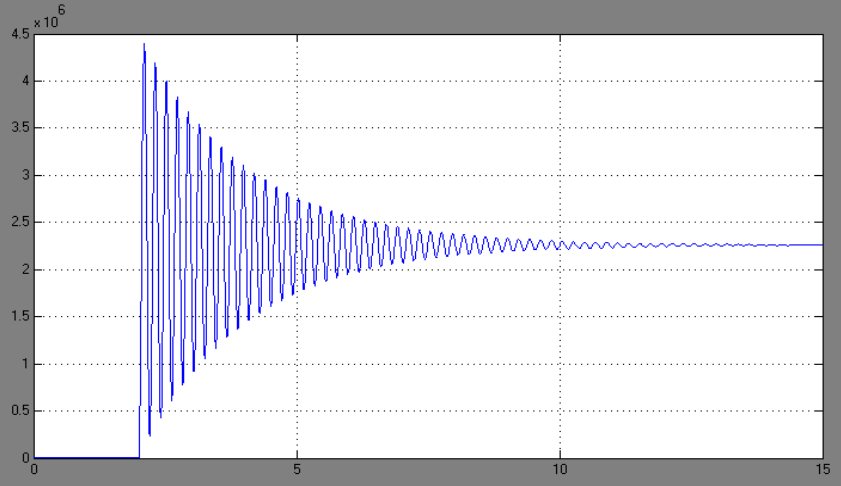
Рисунок 8.4 – График переходного процесса упругого момента.

8.2 Анализ результатов моделирования

Исходя из графиков переходных е обходи можно сделать е об, что САУ не удовлетворяет требованиям технологического процесса. В частности, необходимо снизить колебательность и изменить время регулирования. Следовательно, необходима коррекция параметров регулятора.

8.3 Оптимизация САУ

Оптимизируем систему методом проб и ошибок, подбирая коэффициент «а» и определяя корни характеристического полинома, добиваемся наиболее оптимального для данной САУ расположения корней.

Построим годограф Михайлова с помощью прикладной программы MathCad:

Рисунок 8.5 – Годограф Михайлова

Воспользуемся методом обратного преобразования Лапласа, с помощью прикладной программы MathCad получаем:

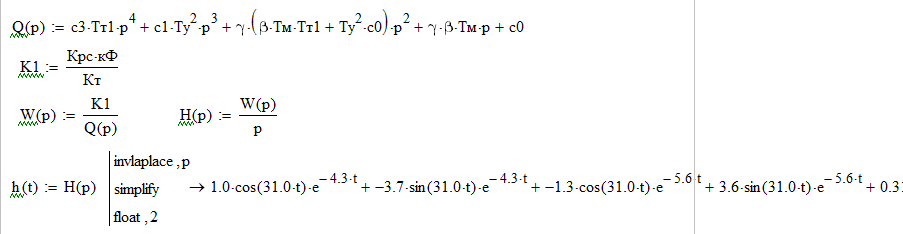
Рисунок 8.6 – График переходного процесса

Показатели качества регулирования оптимизированной САУ

1.Запас устойчивости:

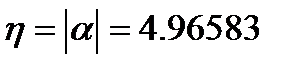
2. Время регулирования:

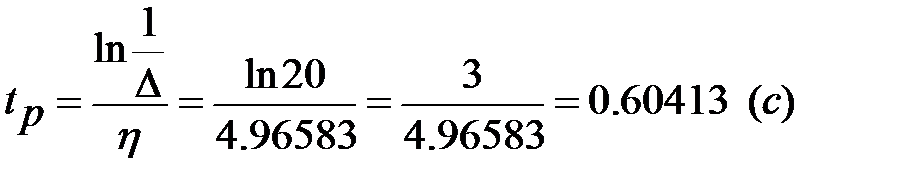
где Δ – ошибка регулирования (Δ = 5%)

3. Колебательность

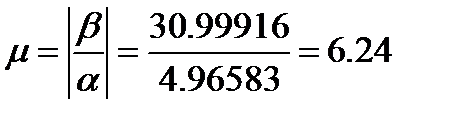
4. Перерегулирование

5. Демфирование

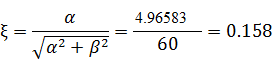
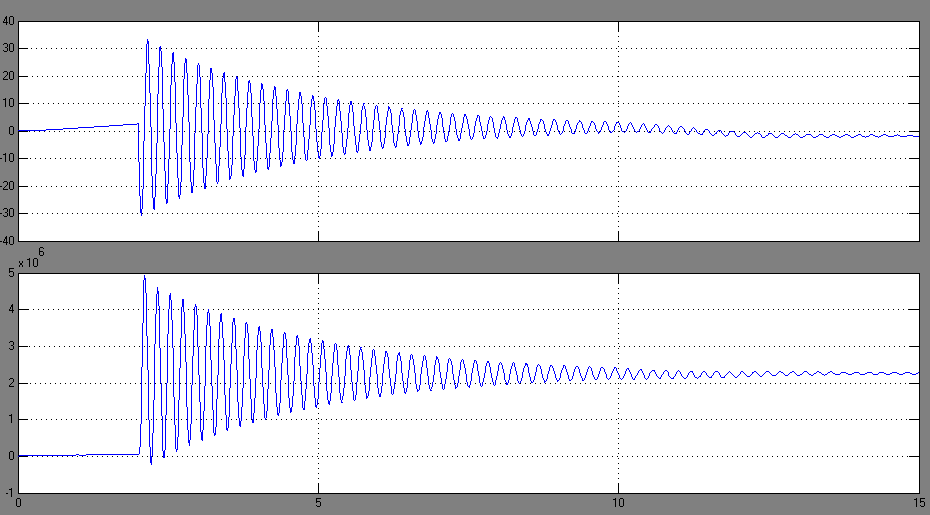
Рисунок 8.8 – График переходного процесса скорости механизма и момента на валу

Рисунок 8.9 – График переходного процесса тока якоря

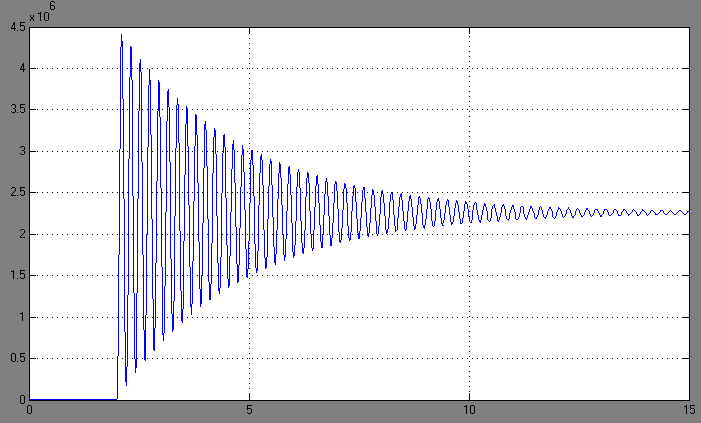
Рисунок 8.10 – График переходного процесса упругого момента.

При анализе получившихся графиков можно заметить, что теоретические данные не совпадают с экспериментальными.

ВЫВОДЫ

В данной расчетно-графической работе была рассчитана система автоматического управления главным приводом блюминга, выполненная по схеме САУ с подчинённым регулированием.

В процессе исследования выяснили, что система получилась устойчивой.

Исходя из расчетов, проведенных на основе исследования корневых показателей качества и показателей качества по кривым ПП, мы можем видеть, что данная САУ имеет близкое к оптимальному время регулирования, но в то же время, имеет довольно большое динамическое и статической падение скорости, так же большое значение колебательности и перерегулирования, что является не удовлетворительным для требований технологического процесса. Это все говорит о том, что данная САУ требует дальнейшей оптимизации и корректировки.

СПИСОК ЛИТЕРАТУРЫ

1. Задорожний Н. А. «Методические указания к выполнению курсовой работы по дисциплине «Теория автоматического управления»», ДГМА; Краматорск, 2006 г.

2. Задорожний Н. А., Задорожняя И. Н. «Анализ и синтез электромеханических систем управления приводом машин с упругими механическими связями», ДГМА; Краматорск, 2010 г.

3. Бесекерский В. А., Попов Е. П. «Теория систем автоматического управления»; издательство «Наука», Москва, 1975 г.

4. Бесекерский В. А., Герасимов А. Н., Лучко С. В. «Сборник задач по теории автоматического управления и регулирования», Издательство «Наука», Москва, 1978 г.

5. Хомяк А., Светличный А., Зайченко С., Федоряк Р. «Система прямого цифрового управления главным приводом блюминга», Кривой Рог, 2004 г.

Дата добавления: 2015-08-31