Модель движения космической станции в поле силы тяжести Земли, Луны и Солнца

Лабораторная работа №3

Чтобы решить задачу, необходимо для начала четко себе ее представить.

Предположим, всеми правдами и неправдами нам удалось заполучить двумерный участок безвоздушного пространства с находящимися в нем телами. Все тела перемещаются под действием сил гравитации [13]. Внешнего воздействия нет.

Необходимо построить процесс их движения относительно друг друга. Простота реализации и красочность конечного результата послужат стимулом и наградой. Освоение Питона будет хорошей инвестицией в будущее.

Введем систему координат [14].

Пусть система состоит из двух тел:

1. массивной звезды массой М и центром ;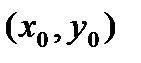

2. легкой планеты массой m, с центром в точке 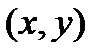, скоростью 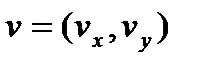и ускорением .

После разбора данного случая, студент легко перейдет к сложным системам со взаимным влиянием звезд и планет друг на друга.

Согласно Второму закону Ньютона:

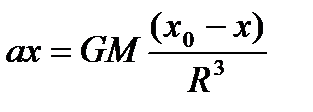
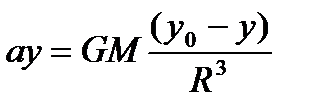
Это позволяет составить алгоритм перемещения планеты в поле гравитации звезды [15]:

1. Перед началом задается начальное положение планеты 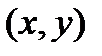и начальную скорость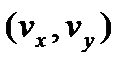

2. На каждом шаге вычисляется новое ускорение по формуле выше, после этого пересчитываем скорость и координаты:

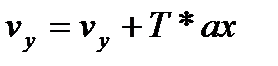
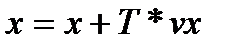
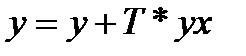
Лабораторная работа №4

1. Целесообразно до начала компьютерной реализации модели провести обезразмеривание переменных, входящих в уравнения, выявить безразмерные комбинации параметров модели и дальнейшие действия производить в безразмерных величинах.

2. Необходим контроль точности результатов и устойчивости применяемого численного метода. Для этого достаточно ограничиться эмпирическими приемами (например, сопоставлением решений, полученных с несколькими разными шагами по времени).

3. Целесообразно применять для моделирования стандартные методы интегрирования систем дифференциальных уравнений, описанные в математической литературе. Простейшие методы (метод Эйлера) часто бывают неустойчивы и их применение ведет к лишнему расходу времени.

4. Результаты моделирования следует выводить на экран компьютера в следующих видах: таблицы зависимостей перемещения и скорости от времени, графики этих зависимостей, траектории. Желательны динамические иллюстрации движения тел (скажем, изображение движений по траекториям в некотором условном масштабе времени через равные промежутки). Уместны звуковые сигналы (одни — в критические моменты для моделируемого движения, другие — через некоторый фиксированный отрезок пройденного пути и т.д.).

5. При выводе результатов в табличном виде следует учитывать, что соответствующий шаг по времени не имеет практически ничего общего с шагом интегрирования и определяется удобством и достаточной полнотой для восприятия результатов на экране. Экран, сплошь забитый числами, не поддается восприятию. Выводимые числа следует разумным образом форматировать, чтобы незначащие цифры практически отсутствовали.

6. При выводе результатов в графической форме графики должны быть построены так, как это принято в математической литературе (с указанием того, какие величины отложены по осям, масштабами и т.д.).

7. Поскольку таблицы, графики и траектории на одном экране обычно не помещаются, удобно сделать меню, в котором пользователь выбирает желаемый в настоящий момент вид представления результатов.

Ход лабораторной работы:

1)

Рис. 12 – Главная форма приложения Space

Запустите приложение Space (рис. 12).

2) В Главном меню выберите Файл – Открыть – Найдите файл с системой – Откройте файл с системой.

Запустите стандартную модель – Главное меню – Модель – Запуск (рис. 13)

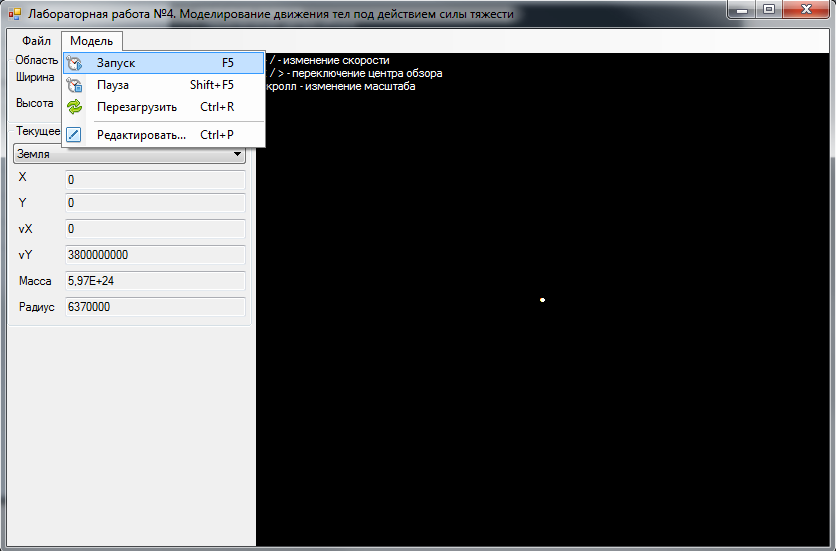
Рис. 13 – Запуск модели в приложении Space

Воспользуйтесь клавишами «+», «-», «>», «<».

Опишите свои наблюдения.

3) Выберите Запустите стандартную модель – Главное меню – Модель – Пауза.

4) Выберите Запустите стандартную модель – Главное меню – Модель – Редактировать.

В окне параметров системы (рис. 14) введите полученные на Практической работе №1 данные для реальной модели движения системы ИСЗ – Луна – Солнце – Земля [16].

Опишите свои наблюдения.

Какие выводы можно сделать о начальном состоянии системы?

Попытайтесь создать собственную модель на основе расчетов для выбранной системы, выполненных на Практической работе №1.

Рис. 14 – Окно параметров системы в приложении Space

Дополнительные задания к лабораторной работе

1. Выписать математическую модель, определить состав набора входных параметров и их конкретные числовые значения [17].

2. Если моделирование будет производиться в безразмерных переменных (решение — на усмотрение студента и преподавателя), то произвести обезразмеривание и найти набор значений безразмерных параметров.

3. Спроектировать пользовательский интерфейс программы моделирования, обращая особое внимание на формы представления результатов.

4. Выбрать метод интегрирования системы дифференциальных уравнений модели, найти в библиотеке стандартных программ или разработать самостоятельно программу интегрирования с заданной точностью.

5. Произвести отладку и тестирование полной программы.

6. Выполнить конкретное задание из своего варианта работы.

7. Качественно проанализировать результаты моделирования.

8. Создать текстовый отчет по лабораторной работе, включающий:

* титульный лист (название работы, исполнитель, группа и т.д.);

* постановку задачи и описание модели;

* результаты тестирования программы;

* результаты, полученные в ходе выполнения задания (в различных формах);

* качественный анализ результатов.

Варианты

Вариант 1

Проверить в компьютерном эксперименте выполнимость второго закона Ньютона.

Вариант 2

Проверить в компьютерном эксперименте выполнимость третьего закона Кеплера, определяющего движение небесных тел по замкнутой траектории.

Вариант 3

Промоделировать траекторию движения малого космического аппарата, запускаемого с борта космической станции, относительно Земли. Запуск осуществляется путем толчка в направлении, перпендикулярном плоскости орбиты движения станции.

Вариант 4

Как будет выглядеть полет искусственного спутника Земли, если учесть возмущающее действие Луны?

Вариант 5

Разработать и реализовать модель движения искусственного спутника Земли при учете воздействия на него малой постоянной силы, обусловленной «солнечным ветром». Считать, что плоскость орбиты движения спутника изначально перпендикулярна «солнечному ветру».

Вариант 6

Считая, что движение Луны вокруг Земли происходит практически по круговой орбите, проанализировать воздействие на эту орбиту со стороны Солнца для малого участка движения, на котором плоскость орбиты перпендикулярна оси «Солнце-Земля».

Вариант 7

Проанализировать особенности движения искусственного спутника Земли, движущегося по практически круговой орбите на высоте порядка 300 км, связанные с малым сопротивлением атмосферы.

Практическая работа 2

Цель: исследовать зависимость формы траектории от величины и направления начальной скорости.

Ход работы:

1. а) По форме траектории движения определить экспериментальным путем величину 1, 2, 3 космических скоростей ИСЗ при следующих условиях:

H = 9000000м

φ = 0˚00’

α = 0˚00’

б) Определить интервалы величин скоростей для параболической и эллиптической орбит.

Форма траектории
	круговая	эллиптическая	параболическая	гиперболическая
Величина скорости

2. Исследовать зависимость формы траектории ИСЗ от направления начальной скорости при следующих условиях

H = 9000000м

φ = 0˚00’

α = 0˚; α = 30˚; α = 45˚; α = 60˚; α = 90˚

V = 7900 м/с

Направление скорости (угол α)	0˚	30˚	45˚	60˚	90˚
Форма траектории

1. Сделать выводы

a) Как изменяется форма траектории ИСЗ в зависимости от изменения величины начальной скорости?

б) Как изменяется форма траектории ИСЗ в зависимости от изменения направления начальной скорости?

Заключение

Неотъемлемой частью обучения моделированию является модельный эксперимент. Основная цель организации каждого модельного эксперимента - это реализация эффективного моделирования. Она связывается с машинным временем - значительный объем обработки в модели повышает стоимость моделирования и понижает эффективность. Для каждой реальной системы часто приходится создавать множество разных моделей, отличающихся способом декомпозиции и уровнем детализации, методом моделирования, средствами программной реализации и т.д. Из множества сходных моделей необходимо выбрать самый эффективный вариант.

Описание теоретической части исследования показало, что существенное значение для достижения достаточной эффективности модели имеет полнота формальной системы абстрактного представления концептуальной модели, простота терминов описания, разработка оптимального плана и др. Применение универсальных программных систем отличается отсутствием специфических языковых операторов, поэтому они являются подходящими прежде всего для аналитического моделирования.

В ходе исследования был проведен детальный анализ обработки информации при компьютерном моделировании, в результате которого были выделены основные моменты изложения теоретического материала. Выделены особенности компьютерных вычислений в качестве объекта изучения при обучении моделированию. На основе всех проведенных исследований были разработаны практические и лабораторные задания для обучения компьютерному моделированию. Для выполнения отдельной лабораторной работы было разработано приложение для моделирования движения ИСЗ. Полученная база знаний была успешно применена при апробации.

Подводя итоги, можно сделать вывод о том, что в ходе работы над дипломным проектом все поставленные в начале исследования задачи, были решены.

Список литературы

1. Романски Р. Математическое моделирование и исследование стохастических временных характеристик процессов компютерной обработки данных // Информационные технологии. - Москва, Россия, 2001, No 2, - С. 51 - 55.

2. Рузавин Г. И. Методология научного познания. ­– М.: 2012 г. – 412 с.

3. Рыбаков Д.С., Дергачёва Л.М. Компьютерное моделирование: задачи оптимизации // Вестник российского университета дружбы. – 2007. – № 2-3.

4. Майер Р.В. Компьютерное моделирование: Учебник для студ. пед. вузов. - Глазов: ГГПИ, 2014. – 531 c.

5. Булавин Л.А., Выгорницкий Н.В., Лебовка Н.И. Компьютерное моделирование физических систем. – Долгопрудный: Издательский Дом “Интеллект”, 2011. – 352 c.

6. Калиткин Н.Н. Численные методы. – БХВ-Петербург, 2011. – 592 с.

7. Ращиков В.С., Рошаль А.С. Численные методы решения физических задач: Учебное пособие. –– СПб: Издательство “Лань”, 2005. – 208 с.

8. Майер Р.В. Компьютерное моделирование физических явлений. – Гла- зов, ГГПИ: 2009. – 112 с.

9. Гулд Х., Тобочник Я. Компьютерное моделирование в физике: В 2-х частях. Часть 1. – М.: Мир, 1990. – 350 с.

10. Бордовицына Т.В. Современное состояние теории движения искусственных спутников Земли. М.: Томский Государственный Университет, 2012. – с. 2–4

11. Васильев А.Н. Научные вычисления в Microsoft Excel. – М.: Издательский дом “Вильямс”, 2004.– 512 с.

12. Гельман В.Я. Решение математических задач средствами Excel: Практикум. – СПб.: Питер, 2003. – 240 с.

13. Майер Р.В. Задачи, алгоритмы, программы [Электронный ресурс] / Глазов: ГГПИ, 2011.URL: http://maier–rv.glazov. net (http://mayer.hop.ru)

14. Майер Р.В. Компьютерное моделирование физических явлений. – Глазов, ГГПИ: 2009. – 112 с.

15. Кушниренко А.Г., Лебедев Г.В, Сворень Р.А - Основы информатики и вычислительной техники. 2002 – 323 с.

16. Майер Р.В. Решение физических задач с помощью электронных таблиц MS Excel // International Journal of Open Information Technologies -- vol. 2, - no. 9, - 2014. – С. 18-23.

17. Майер Р.В. Решение физических задач с помощью электронных таблиц MS Excel // International Journal of Open Information Technologies -- vol. 2, - no. 9, - 2014. – С. 18-23.

18. Самарский А.А. Математическое моделирование: Идеи. Методы. Примеры /А.А.Самарский, А.П.Михайлов. – М.: Физматлит, 2001.– 320 с.

19. Старовиков М.И. Введение в экспериментальную физику: Учебное пособие. – Спб.: Издательство “Лань”, 2008. – 240 с.

20. Угринович Н.Д. Исследование информационных моделей. Элективный курс: Учебное пособие. – М.: БИНОМ. Лаборатория знаний, 2004. – 183 с.

21. Угринович Н.Д. Разработка информационных моделей. Элективный курс: Учебное пособие. – М.: БИНОМ., 2004. – 202 с.

22. Кострюков С. А., Максимов В. Е., Пешков В. В., Шунин Г. Е. Метод конечных элементов в компьютерном моделировании физико-технических систем. // Оптимизация и моделирование в автоматизированных системах: Межвуз. сб. научн. тр. Воронеж: Изд. ВГТУ, 1997. с. 136 – 141

23. Е. И. Бутиков. Основы классической динамики и компьютерное моделирование. Материалы научно-методической конференции, Академическая Гимназия, Санкт-Петербург -Старый Петергоф, 1998 – с. 47.

24. А. Ф. Кавтрев. "Методика использования компьютерных моделей на уроках физики". Пятая международная конференция "Физика всистеме современного образования", тезисы докладов, том 3,Санкт-Петербург: "Изд-во РГПУ им. А. И. Герцена", 2009 – с. 98-99.

25. П. И. Белостоцкий, Г. Ю. Максимова, Н. Н. Гомулина "Компьютерные технологии: современный урок физики и астрономии". Газета "Физика", 2009 – с. 3.

Дата добавления: 2015-08-31