Формирование сигналов с амплитудной модуляцией

Введение

В данной статье речь пойдет о разновидностях аналоговой амплитудной модуляции. Предполагается, что читатель понимает смысл комплексной огибающей полосового радиосигнала, а также понятия аналитического сигнала и преобразования Гильберта.

Как было отмечено ранее, процесс модуляции заключается в формировании низкочастотной комплексной огибающей

(1)

после чего производится перенос этой комплексной огибающей на несущую частоту умножением на

(2)

Также было отмечено, что все виды модуляции различаются только способом формирования комплексной огибающей на основе модулирующего сигнала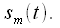

Рассмотрим как производится формирование комплексной огибающей в случае с амплитудной модуляцией (АМ).

При АМ производится изменение только амплитуды несущего колебания при постоянной начальной фазе:

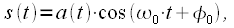
(3)

где 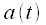- закон изменения амплитуды, а - постоянная начальная фаза несущего колебания. Потребуем, чтобы модулирующий сигнал имел нулевую постоянную составляющую и 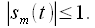Тогда где 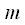носит название глубины АМ и радиосигнал с АМ имеет вид:

(4)

Поясним смысл глубины АМ, для этого возьмем частный случай модулирующего сигнала где В этом случае получим так называемую однотональную АМ. При амплитуда несущего колебания не меняется. На рисунках 1 - 4 приведены графики АМ сигнала при различной глубине модуляции: от 0 до 1,5. Синим показана амплитуда При глубине модуляции от 0 до 1 амплитуда несущего колебания совпадает с 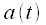, однако при наблюдается перемодуляция, так как 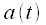пересекает ось абсцисс.

Рисунок 1: АМ сигнал при глубине модуляции равной 0

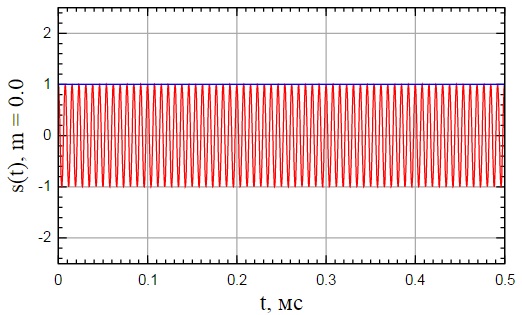Рисунок 2: АМ сигнал при глубине модуляции равной 0,5 Рисунок 3: АМ сигнал при глубине модуляции равной 1 Рисунок 4: АМ сигнал при глубине модуляции равной 1,5

Если глубина АМ выбрана так, что перемодуляции не наблюдается, то измерить глубину АМ можно по осциллограмме радиосигнала. Для этого необходимо померить максимальную и минимальную амплитуду несущего колебания как это показано на рисунке 5, и по ним рассчитать глубину АМ по формуле:

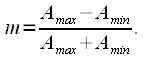
(5)

Рисунок 5: Измерение глубины АМ по осциллограмме радиосигнала

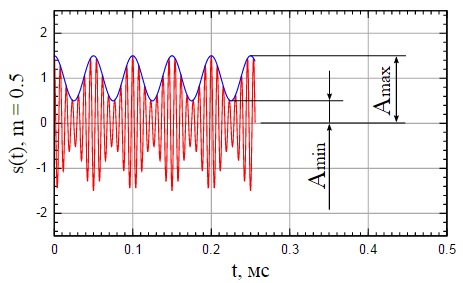
Необходимо отметить, что перемодуляция вредный эффект, которого необходимо избегать, в противном случае возникнут проблемы при демодуляции сигнала.

Теперь рассмотрим структурную схему АМ модулятора. Для этого выделим из АМ сигнала (4) комплексную огибающую:

(6)

Таким образом, комплексная огибающая равна 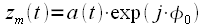, тогда квадратурные составляющие комплексной огибающей равны:

(7)

Тогда структурная схема АМ модулятора на базе универсального квадратурного модулятора может быть представлена как это показано на рисунке 6.

Рисунок 6: Структуреная схема АМ модулятора

Данная схема не является оптимальной, ее можно упростить, задав фазу комплексной огибающей равную нулю, тогда

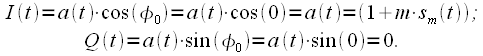
(8)

Таким образом, квадратурная составляющая не учитывается, и радиосигнал формируется простым умножением несущего колебания на как это показано на рисунке 7.

Рисунок 7: Упрощенная схема АМ

Дата добавления: 2015-08-31