Понятие о производной спектрофотометрии

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Айситулина К. Тренинги персонала в ресторане. - М.: Ресторанные ведомости, 2008.

2. Акурова Н., Крупцов А. Азбука ресторанного сервиса. - М: Дело, 2004.

3. Аренков И.А. Маркетинговые исследования: основы теории и методики. - СПб.: СПбУЭФ, 1992.

4. Багиев Г.Л. Методы получения и обработки маркетинговой информации. - СПб.: СПбУЭФ, 1996.

5. Багиев Г.Л., Аренков И. А. Основы маркетинговых исследований. - СПб.: СПбУЭФ,1996.

6. Бандурин А.В., Чуб Б.А. Стратегический менеджмент организации. - М.: Изд-во Михайлова В.А. 2000.

7. Батраева Э.А. Изучение спроса в общественном питании: теория и практика: Монография. Красноярск: КрасГУ, 2002.

8. Беляевский И.К. Маркетинговое исследование: информация, анализ, прогноз: Учеб. пособие. - М.: Финансы и статистика, 2001.

9. Богатин Ю. В., Швандар В.А. Экономическое управление бизнесом: Учеб. пособие для вузов. - М.: Юнити-Дана, 2001.

10. Болт Г.Дж. Практическое руководство по управлению сбытом. Пер.с англ. / Науч.ред. и авт.предисловия Ф.А. Крутиков. - М.: Экономика, 2000.

11. Большаков А.С., Михайлов В.И. Современный менеджмент: теория и практика. - СПб.: Питер, 2002.

12. Бородина В.В. Ресторанно-гостиничный бизнес. Маркетинг и менеджмент. - М.: Книжный мир, 2002.

13. Бороноева Т.А. Современный рекламный менеджмент. - М.: Аспект Пресс, 2002.

Производную спектрофотометрию относят к одному из вариантов дифференциальной спектрофотометрии. Если в описанном выше варианте дифференциальной спектрофотометрии используют разность оптических плотностей при одной и той же длине волны l = const (А_х = e l(c_x – c₀)), то в производной спектрофотометрии также измеряют разность светопоглощения, но при двух длинах волн l₁ и l₂, разделенных небольшим интервалом Dl = l₂ - l₁.

Предел отношения разности оптических плотностей DА = А₂ – А₁ соответственно при двух длинах волн l₂ и l₁к Dl равен математической первой производной

и представляет собой некоторую функцию f(l) от длины волны.

В производной спектрофотометрии определяют математические производные от оптической плотности по длине волны

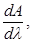
и т. д.

(чаще всего — не выше второй производной) и строят график спектральной кривой в координатах

, и т. д.

откладывая по оси абсцисс длину волны, а по оси ординат — первую или вторую производную (иногда — производные более высокого порядка).

В методе определяют также производные от оптической плотности не только по длине волны, но и по волновому числу v (или по частоте) и получают соответствующие спектральные кривые в координатах производная по волновому числу (ось ординат) — волновое число (ось абсцисс). Достоинство рассматриваемого метода состоит в том, что на спектральных кривых, записанных в координатах производная — длина волны (или производная — волновое число), отчетливо получаются полосы, проявляющиеся лишь в виде скрытых максимумов и нечетких перегибов на полосе поглощения при обычном представлении спектральной кривой в координатах оптическая плотность (или коэффициент погашения) – длина волны. Такие полосы на спектральных кривых производных можно использовать как в качественном анализе (идентификация веществ по спектру), так и при количественном определении веществ в растворах (c использованием в качестве аналитической полосы максимумов на производных спектральных кривых), в том числе компонентов смесей без их предварительного разделения.

Величина первой производной пропорциональна крутизне наклона; исходной спектральной кривой A = f(l), а точки пересечения кривой первой производной с осью длин волн отвечают максимумам или минимумам на исходной спектральной кривой. При этом форма производной кривой усложняется: максимуму на исходной спектральной кривой А = f(l) соответствуют положительный и отрицательный максимумы на кривой dA/dl = f(l).

На кривой второй производной максимуму в исходном спектре А = f(l) соответствует также максимум, но взятый с обратным знаком. К тому же вторая производная позволяет фиксировать две соседние полосы поглощения, разделенные меньшим интервалом длин волн. Поэтому на практике чаще предпочитают пользоваться спектральной кривой второй производной, чем первой.

Производные спектральные кривые получают либо численными методами дифференцирования, либо непосредственно на регистрирующем спектрофотометре, если на нем предусмотрена запись кривых производных (например, с использованием дифференцирующих приставок к саморегистрирующим спектрофотометрам).

Вид спектральных кривых существенно зависит от величины интервала Dl, используемого в расчетах кривой производной. В случае широких полос поглощения в исходных спектрах А = f(l) спектральную кривую производной рассчитывают для интервала Dl = 2; 4; 6 и 8 нм; оптимальный интервал составляет 4 нм.

На рис. 5 приведены спектральные кривые для раствора лекарственного препарата теофиллина в координатах Е — l (а) и d² А / dl² — l (б), где Е — удельный коэффициент погашения теофиллина в растворе. При этом кривая второй производной построена с интервалом Dl = 4 нм.

Двум отчетливым максимумам в спектре поглощения раствора теофиллина отвечают два столь же отчетливые минимумы (отрицательные максимумы) на кривой второй производной. Кроме того, на этой кривой проявляются и малоинтенсивные скрытые максимумы.

Рис. 5. Спектр поглощения (а) и спектральная кривая второй производной (б), построенная с интервалом Dl = 4 нм, раствора теофиллина

Рис. 6. Спектр поглощения (1) и спектральная кривая второй производной (2) раствора смеси амидопирина и дибазола

Метод позволяет идентифицировать скрытые максимумы в спектре раствора смесей. На рис. 6 в качестве примера представлены спектр поглощения раствора смеси лекарственных препаратов амидопирина с дибазолом и спектральная кривая второй производной для того же раствора. Полосы обоих компонентов, включая скрытые максимумы, четко проявляются на кривой второй производной и могут быть использованы для определения компонентов в их смеси.

На рис. 7 показана спектральная кривая четвертой производной для смеси амидопирина и дибазола. Скрытые максимумы и перегибы проявляются на ней еще более отчетливо, чем на спектральной кривой второй производной, что может быть использовано для идентификации дибазола в лекарственных формах.

Переход к производным кривым более высокого порядка повышает случайные ошибки фотометрических определений.

Разработаны многочисленные методики, использующие производную спектрофотометрию для идентификации и определения различных веществ, особенно — лекарственных препаратов. Так, по первым производным предложено анализировать смесь теобромина и салицилата натрия, бутамида в трехкомпонентной смеси. По вторым производным идентифицируют дибазол, кофеин, папаверина гидрохлорид, теобромин, теофиллин; определяют амидопирин, атропин, бензотропин, бутадион, дифенилгидантоин, кофеин, нифуроксим и фуразолидон при совместном присутствии, папаверина гидрохлорид, парацетамол, стрептомицин, теофиллин и др. По четвертой производной определяют дибазол.

Методами производной спектрофотометрии анализируют также соединения урана (VI) в присутствии солей железа; соединения редкоземельных элементов и т.д. [2]

Дата добавления: 2015-08-31