Анализ алгоритма

6 0 0 0 0 0 0 0 1 1

5 0 0 1 0 1 0 1 0 1

4 0 0 0 0 0 1 1 1 0

3 0 1 0 1 0 1 0 0 0

2 1 0 0 1 1 0 0 0 0

6 0 0 0 0 0 1 -1

5 0 0 0 0 -1 -1 1

4 0 0 0 1 1 0 0

3 0 1 -1 -1 0 0 0

{1,2}

{1,3}

{1,5}

{2,3}

{2,5}

{3,4}

{4,5}

{4,6}

{5,6}

(б) 1 1 1 1 0 0 0 0 0 0

Рисунок 1. а) Ориентированный граф и его матрица инциденций;

б) Неориенти­рованный граф и его матрица инциденций.

где b_ij = 1, если существует ребро, идущее из вершины х в вер­шину у, и b_ij = 0 в противном случае. Здесь мы подразумеваем, что ребро {х, у} неориентированного графа идет как от х к у, так и от у к х, так что матрица смежности такого графа всегда является симметричной. Это проиллюстрировано на рисунке 2.

Основным преимуществом матрицы смежности является тот факт, что за один шаг можно получить ответ на вопрос «су­ществует ли ребро из х в y?». Недостатком же является тот факт, что независимо от числа ребер объем занятой памяти составляет n². На практике это неудобство можно иногда уменьшить, храня целую строку (столбец) матрицы в одном машинном слове — это возможно для малых n.

В качестве еще одного аргумента против использования матрицы смежности приведем теорему о числе шагов, которое должен выполнить алгоритм, проверяющий на основе матрицы смежности некоторое свойство графа.

Пусть Р — некоторое свойство графа P(G) = 0 или P(G)=1 в зависимости от того, обладает или не обладает G на­шим свойством. Предположим, что свойство Р удовлетворяет следующим трем условиям:

(а) P(G)=P(G'), если графы G и G' изоморфны;

(б) P(G) = 0 для произвольного пустого графа <V,Æ> и P(G)=1 для произвольного полного графа <V, P₂(V)> с до­статочно большим числом вершин;

1 2 3 4 5 6 1 2 3 4 5 6

1 0 1 1 0 0 0 1 0 1 1 0 1 0

2 0 0 0 0 0 0 2 1 0 1 0 1 0

3 0 1 0 1 0 0 3 1 1 0 1 0 0

4 0 0 0 0 0 0 4 0 0 1 0 1 1

5 0 0 0 1 0 1 5 1 1 0 1 0 1

6 0 0 0 0 1 0 6 0 0 0 1 1 0

Рисунок 2. Матрицы инциденций для графов на рисунке 1.

(в) добавление ребра не нарушает свойства Р, т. е. P(G)<P(G') для произвольных графов G=(F,E) и G'=(V, E'), таких что Е = Е'.

Примером такого свойства Р является существование цикла (в графе, имеющем, по крайней мере три вершины).

Теорема. Если Р — свойство графа, отвечающее условиям (а), (б), (в), то каждый алгоритм, проверяющий свойство Р (т. е. вычисляющий значение P(G) для данного графа G) на основе матрицы смежности, выполняет в худшем случае Ω(n²) шагов, где n — число вершин графа.

Эта теорема справедлива также для ориентированных гра­фов и для свойств, не зависящих от петель графа, т, е. отве­чающих дополнительному условию

(г) P(G) = P(G') для произвольных ориентированных гра­фов G = < V, E>, G’ = < V, Е> U <v, v>>, v C V.

Более экономным в отношении памяти (особенно в случае, неплотных графов, когда m гораздо меньше n2) является ме­тод представления графа с помощью списка пар, соответствующих его ребрам. Пара <x, у> соответствует дуге <х, у>, если граф ориентированный, и ребру {х, y} - в случае неориентиро­ванного графа.

Рисунок 3. Списки ребер соответствующие графам на рисунке 1.

Очевидно, что объем памяти в этом случае составляет 2n. Неудобством является большое число шагов — порядка n в худшем случае, — необходимое для по­лучения множества вершин, к которым ведут ребра из данной вершины.

Ситуацию можно значительно улучшить, упорядочив множество пар лексикографически и применяя двоичный поиск, но лучшим решением во многих случаях оказывается структура данных, которую мы будем называть списками инцидентности. Она содержит для каждой вершины v C V список вершин и, таких что v -> u (или v — и в случае неориентированного гра­фа). Точнее, каждый элемент такого списка является записью u, содержащей вершину u. строка и указатель u. след на сле­дующую запись в списке (u. след = nil для последней записи в списке). Начало каждого списка хранится в таблице НАЧАЛО; точнее, НАЧАЛО[v] является указателем на начало спи­ска, содержащего вершины из множества {u: v+u} ({u: v - u} для неориентированного графа). Весь такой список обычно не­формально будем обозначать 3AПИСЬ[v], а цикл, выполняю­щий определенную операцию для каждого элемента и из этого списка в произвольной, но четко установленной последователь­ности, соответствующей очередности элементов в списке, будем записывать «for u C ЗАПИСЬ [v] do...».

Отметим, что для неориентированных графов каждое ребро {u, v} представлено дважды: через вершину v в списке ЗАПИСЬ[u] и через вершину u в списке ЗАПИСЬ[v]. Во многих алгоритмах структура графа динамически модифицируется добавлением и удалением ребер. В таких случаях полагаем, что в наших списках инцидентности элемент списка ЗАПИСЬ [u], содержащий вершину u, снабжен указателем на элемент спи­ска 3AПИCЬ[v], содержащий вершину u, и что каждый эле­мент списка содержит указатель не только к следующему эле­менту, но и к предыдущему. Тогда удаляя некоторый элемент из списка, можем легко за число шагов, ограниченное кон­стантой, удалить другой элемент, представляющий то же са­мое ребро, не просматривая список, содержащий этот элемент.

Аналогичным способом определяем для каждой вершины и неориентированного графа список ПРЕДШ[v], содержащий вершины из множества (u: u -> v).

Число ячеек памяти, необходимое для представления графа с помощью списков инцидентности, будет, очевидно, иметь по­рядок m + n. На рисунке 4 представлены списки инцидентности, соответствующие графам на рисунке 1.

(б)  

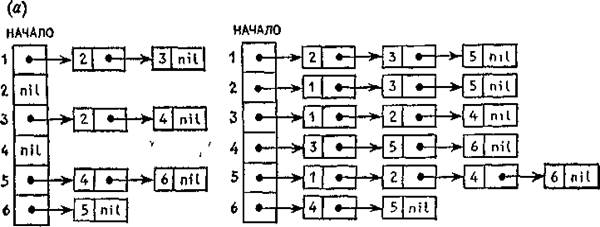
Рисунок 4. Списки инцидентности ЗАПИСЬ[v], v =V, соответствующие графам на рисунке 1.

Рассмотрим метод поиска в графе, называемый поиском в ширину (англ.: breadth first search). Прежде чем описать его, отметим, что при поиске в глубину, чем позднее будет посещена вершина, тем раньше она будет использована — точнее, так будет при допущении, что вторая вершина посещается перед использованием первой. Это прямое следствие того факта, что просмотренные, но еще не исполь­зованные вершины скапливаются в стеке. Поиск в ширину, грубо говоря, основывается на замене стека очередью. После такой модификации, чем раньше посещается вершина (поме­щается в очередь), тем раньше она используется (удаляется из очереди). Использование вершины происходит с помощью про­смотра сразу всех еще не просмотренных соседей этой вершины. Вся процедура поиска представлена ниже (данная процедура используется также и для просмотра графа, и в псевдокоде, описанном ниже, отсутствуют операторы, которые не используются для поиска).

1 procedure WS (v);

(*поиск в ширину в графе с началом в вершине v;

переменные НОВЫЙ, ЗАПИСЬ — глобальные *)

2 begin

3 ОЧЕРЕДЬ:= Æ; ОЧЕРЕДЬ <= v; НОВЫЙ [v]:= ложь

4 while ОЧЕРЕДЬ ¹ Æ do

5 begin р<= ОЧЕРЕДЬ; посетить р;

6 for u Î ЗАПИСЬ [р] do

7 if НОВЫЙ [u] then

8 begin ОЧЕРЕДЬ <= u; НОВЫЙ [u]:=ложь

9 end

10 end

11 end

Примечание: в 7-й строке псевдокода кроме условия НОВЫЙ[u] должно также выполниться условие наличия связи (ребра) между v-й и u-й вершинами. Для установки наличия ребра сначала в списке v-й вершины ищется информационное значение u-й вершины. Если оно найдено, то ребро установлено, если нет, то информационное значение v-й вершины ищется в списке u-й вершины, т.е. наоборот. В результате добавления двух лишних циклов поиска общий алгоритм поиска несколько теряет компактность, но на быстродействии в целом это не сказывается.

1 procedure Write_S;

2 begin

3 for v Î V do НОВЫЙ[u]:= истина; (* инициализация *)

4 for v Î V do

5 if HOBЫЙ[v] then WG(v)

6 end

Способом, аналогичным тому, какой был применен для по­иска в глубину, можно легко показать, что вызов процедуры WS(v) приводит к посещению всех вершин связной компоненты графа, содержащей вершину v, причем каждая вершина про­сматривается в точности один раз. Вычислительная сложность поиска в ширину также имеет порядок О(m + n), так как каждая вершина помещается в очередь и удаляется из очереди в точ­ности один раз, а число итераций цикла 6, очевидно, будет иметь порядок числа ребер графа.

В очереди помещены сначала вершины, находящиеся на расстоянии 0 от v (т. е. сама вершина v), затем поочередно все новые вершины, достижимые из v, т. е. вершины, находя­щиеся на расстоянии 1 от v, и т. д. Под расстоянием здесь мы понимаем длину кратчайшего пути. Предположим теперь, что уже рассмотрели все вершины, находящиеся на расстоянии, не превосходящем r, от v, что очередь содержит все вершины, находящиеся от v на расстоянии r, и только эти вершины. Использовав каждую вершину р, находящую­ся в очереди, наша процедура просматривает некоторые новые вершины, и каждая такая новая вершина u находится, оче­видно, на расстоянии г + 1 от v. После использования всех вер­шин из очереди, находящихся на расстоянии r от v, она (оче­редь), очевидно, содержит множество вершин, находящихся на расстоянии r + 1 от v, и легко заметить, что условие индукции выполняется и для расстояния r + 1.

На рисунке 5 представлен граф, вершины которого зануме­рованы согласно очередности, в которой они посещаются в про­цессе поиска в глубину.

Как и в случае поиска в глубину, процедуру WS можно использовать без всяких модификаций и тогда, когда списки инцидентности ЗАПИСЬ[v], v = V, определяют некоторый ориентированный граф. Очевидно, что тогда посещаются толь­ко те вершины, до которых существует путь от вершины, с ко­торой мы начинаем поиск.

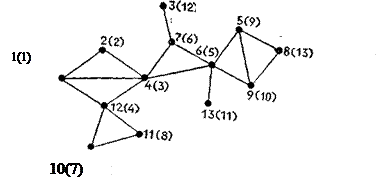Рисунок 5. Нумерация вершин графа (в скобках), соответствующая очередности, в которой они просматриваются в процессе поиска в ширину.

Дата добавления: 2015-08-31