Экстремумы функции одной переменной

2.1. Построить график функции 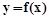, найти наименьшее и наибольшее значение функции и указать, при каких значениях аргумента они достигаются.

2.1.1.

2.1.2.

2.1.3.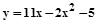

2.1.4.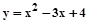

2.1.5. .

2.2. Найти наименьшее и наибольшее значение функции 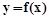, заданной в замкнутом промежутке 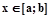и указать, при каких значениях аргумента они достигаются. Предварительно построить график этой функции.

2.2.1.

2.2.2.

2.2.3.

2.2.4.

2.2.5. .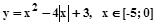

2.3. Решить предлагаемую задачу. По условию задачи сделать чертеж.

2.3.1. Дан D ABC, в котором ÐC = g, а площадь его равна S. Определить длины сторон, образующих ÐC так, чтобы длина стороны, лежащей против ÐC, имела минимально возможную длину.

2.3.2. Из орудия, расположенного под углом a к горизонту, произведен выстрел с начальной скоростью v₀. Определить, при каком значении a дальность полета снаряда будет максимальной, если при этом не учитывать сопротивление воздуха и высоту орудия.

Указание. При решении следует использовать формулы, выражающие зависимость дальности и высоты полета снаряда от времени: дальность полета - ; высота полета - .

2.3.3. Высота четырехугольной пирамиды равна и проектируется в точку пересечения диагоналей прямоугольника, лежащего в его основании. По ребрам пирамиды ползет жук со скоростью 1 см/с. Достаточно ли ему двух секунд, чтобы спуститься с вершины по боковому ребру на основание, если вдоль периметра основания он проползает за 8 секунд?

2.3.4. Определить максимальную площадь участка и его размеры так, чтобы его можно было оградить куском проволоки

данной длины t м.

2.3.5. Из квадратного листа железа шириной 60 см изготовить коробку без крышки так, чтобы вместимость ее была максимальная, а дно квадратное.

2.3.6. Из трех одинаковых досок шириной h см нужно изготовить жолоб с поперечным сечением в форме трапеции.

Как это сделать, чтобы пропускная способность жолоба была наибольшей?

2.3.7. Из всех параллелепипедов с заданной суммой длин трех его взаимно перпендикулярных ребер найти такой,

у которого максимальный объем.

2.3.8. Из всех треугольников с данным основанием длиной a и данным углом при вершине a найти тот,

который имеет максимальную площадь.

2.3.9. Из всех треугольников с данным основанием длиной a и данным углом при вершине a найти тот,

который имеет максимальный периметр.

2.3.10. Из всех конусов, описанных около данного шара, найти такой, объем которого наименьший.

2.3.11. Спортплощадку прямоугольной формы и площадью 810 м² нужно огородить с севера и юга деревянным забором, а с востока и запада - проволочным. Установка 1 м деревянного забора обходится в 500 рублей, а проволочного - в 200 рублей. Определить размеры участка и соответствующие затраты так, чтобы затраты оказались минимальными.

2.3.12. Из куска гранита нужно вырубить постамент в форме прямоугольного параллелепипеда так, чтобы его высота была равна диагонали основания, а площадь основания равна 4 м². Определить длины сторон основания, соответствующие наименьшей площади его поверхности.

2.4. Найти наименьшее и наибольшее значение функции 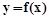, заданной в замкнутом промежутке 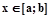и указать, при каких значениях аргумента они достигаются.

2.4.1.

2.4.2. .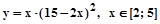

Дата добавления: 2015-07-13