Области применения и ограничения использования линейного программирования для решения экономических задач

Особенно широкое применение методы и модели линейного программирования получили при решении задач экономии ресурсов (выбор ресурсосберегающих технологий, составление смесей, раскрой материалов, производственно-транспортных и других задач). [2, c.92]

Рассмотрим постановку задачи о наилучшем использовании ресурсов. Пусть некоторая производственная единица (цех, завод, объединение и т. д.), исходя из конъюнктуры рынка, технических или технологических возможностей и имеющихся ресурсов, может выпускать n различных видов продукции (товаров), известных под номерами, обозначаемыми индексом j . Товары будем обозначать . Предприятие при производстве этих видов продукции должно ограничиваться имеющимися видами ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов, рабочей силы, оборудования, электроэнергии и т. д.). Все эти виды ограничивающих факторов называют ингредиентами . Пусть их число равно m; припишем им индекс i . Они ограничены, и их количества равны соответственно условных единиц. Таким образом, - вектор ресурсов. Известна экономическая выгода (мера полезности) производства продукции каждого вида, исчисляемая, скажем, по отпускной цене товара, его прибыльности, издержкам производства, степени удовлетворения потребностей и т. д. Примем в качестве такой меры, например, цену реализации 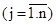, т. е. — вектор цен. Известны также технологические коэффициенты , которые указывают, сколько единиц i–го ресурса требуется для производства единицы продукции j-го вида. Матрицу коэффициентов называют технологической и обозначают буквой А. Имеем . Обозначим через план производства, показывающий, какие виды товаров 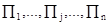нужно производить и в каких количествах, чтобы обеспечить предприятию максимум объема реализации при имеющихся ресурсах. Так как - цена реализации единицы j-й продукции, цена реализованных единиц будет равна , а общий объем реализации примет вид (формула 2.1). Это — целевая функция, которую нужно максимизировать.

(2.1)

Так как - расход i-го ресурса на производство единиц j-й продукции, то, просуммировав расход i-горесурса на выпуск всех n видов продукции, получим общий расход этого ресурса, который не должен превосходить единиц (формула 2.2).

(2.2)

Чтобы искомый план был реализован, наряду с ограничениями на ресурсы нужно наложить условие неотрицательности на объёмы выпуска продукции .

В модель задачи о наилучшем использовании ресурсов входят: целевая функция (формула 2.3), система ограничений (формула 2.4) и условия неотрицательности (формула 2.5)

(2.3)

(2.4)

(2.5)

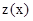Так как переменные входят в функцию и систему ограничений только в первой степени, а показатели являются постоянными в планируемый период, то это – задача линейного программирования.

В различных отраслях народного хозяйства возникает проблема составления таких рабочих смесей на основе исходных материалов, которые обеспечивали бы получение конечного продукта, обладающего определенными свойствами. К этой группе задач относятся задачи о выборе диеты, составлении кормового рациона в животноводстве, шихт в металлургии, горючих и смазочных смесей в нефтеперерабатывающей промышленности, смесей для получения бетона в строительстве и т. д.. Высокий уровень затрат на исходные сырьевые материалы и необходимость повышения эффективности производства выдвигает на первый план следующую задачу: получить продукцию с заданными свойствами при наименьших затратах на исходные сырьевые материалы.

Сущность задачи об оптимальном раскрое состоит в разработке таких технологически допустимых планов раскроя, при которых получается необходимый комплект заготовок, а отходы (по длине, площади, объему, массе или стоимости) сводятся к минимуму. Более сложные постановки ведут к задачам целочисленного программирования.

Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления в n пунктов назначения . При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза. Обозначим через 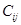тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, через – запасы груза в i-м пункте отправления, через – потребности в грузе в j–м пункте назначения, а через 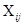– количество единиц груза, перевозимого из i-го пункта отправления в j-й пункт назначения. Тогда математическая постановка задачи состоит в определении минимального значения функции (формула 2.7) при определенных ограничениях (формула 2.8) и условиях неотрицательности (формула 2.9).

(2.7)

(2.8)

(2.9)

Обычно исходные данные транспортной задачи записывают в виде таблицы, которую называют матрицей планирования. (табл. 2.1).

Таблица 2.1

Матрица планирования ТЗ

Поставщики	Потребители	Запасы
B1	B2	…	Bn
A1	C11	C12	…	C1n	a1
A2	C21	C22	…	C2n	a2
…	…	…	…	…	…
Am	Cm1	Cm2	…	Cmn	am
b1	b2	…	bn

Таким образом, обеспечивается доставка необходимого количества груза в каждый из пунктов назначения, вывоз имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки. Всякое неотрицательное решение систем линейных уравнений называется планом транспортной задачи. План, при котором целевая функция принимает свое минимальное значение, называется оптимальным планом транспортной задачи. Если в опорном плане число отличных от нуля компонент равно в точности n+m–1, то план является невырожденным, а если меньше – то вырожденным. [3 c.132-134]

Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, то модель такой транспортной задачи называется закрытой. Если же указанное условие не выполняется, то модель транспортной задачи называется открытой.

В случае превышения запаса над потребностью, вводится фиктивный (n+1)–й пункт назначения с потребностью (формула 2.10) и соответствующие тарифы считаются равными нулю. Аналогично, в случае, если потребности превышают количество запасов, также вводится фиктивный (m+1)–й пункт отправления с запасом груза и тарифы полагаются равными нулю (формула 2.11). Этим задача сводится к обычной транспортной задаче, из оптимального плана которой получается оптимальный план исходной задачи.

(2.10)

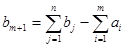(2.11)

Как и для всякой задачи линейного программирования, оптимальный план транспортной задачи является и опорным планом. Опорный планявляется допустимым решением ТЗ и используется в качестве начального базисного решения при нахождении оптимального решения методом потенциалов. Существует четыре метода нахождения опорных планов:

1. метод северо-западного угла;

2. метод минимального элемента;

3. метод двойного предпочтения;

4. метод штрафов (Фогеля).

"Качество" опорных планов, полученных этими методами, различается: в общем случае метод Фогеля дает наилучшее решение (зачастую оптимальное), а метод северо-западного угла– наихудшее.

Все существующие методы нахождения опорных планов отличаются только способом выбора клетки для заполнения. Само заполнение происходит одинаково независимо от используемого метода. Следует помнить, что перед нахождением опорного плана транспортная задача должна быть сбалансирована.

В методе северо-западного угла из всех не вычеркнутых клеток выбирается самая левая и верхняя (северо-западная) клетка. Другими словами, на каждом шаге выбирается первая из оставшихся не вычеркнутых строк и первый из оставшихся не вычеркнутых столбцов.

Для того чтобы заполнить клетку (i,j), необходимо сравнить текущий запас товара в рассматриваемой i-й строке с текущей потребностью в рассматриваемом j-м столбце. Нахождение опорного плана продолжается до тех пор, пока не будут вычеркнуты все строки и столбцы. [3 c.137]

В методе минимального элемента первой клеткой выбирают клетку с наименьшей суммой доставки и заполняют ее максимально возможным грузом.

Если таблица стоимостей велика, то перебор всех элементов затруднителен. В этом случае используют метод двойного предпочтения, суть которого заключается в следующем: в каждой строке и каждом столбце отмечают «V» наименьшую стоимость, а затем клетки с двойным символом «VV» заполняют с учетом наименьшей стоимости. Затем распределяют перевозки по клеткам, отмеченным знаком «V». В оставшейся части таблицы перевозки распределяют по наименьшей стоимости.

На каждом шаге метода Фогеля для каждой i-й строки вычисляются штрафы, как разность между двумя наименьшими тарифами строки. Таким же образом вычисляются штрафы для каждого j-го столбца. После чего выбирается максимальный штраф из всех штрафов строк и столбцов. В строке или столбце, соответствующем выбранному штрафу, для заполнения выбирается не вычеркнутая клетка с минимальным тарифом. Если существует несколько одинаковых по величине максимальных штрафов в матрице, то в соответствующих строках или столбцах выбирается одна не вычеркнутая клетка с минимальным тарифом.

Если клеток с минимальным тарифом также несколько, то из них выбирается клетка (i,j) с максимальным суммарным штрафом, т.е. суммой штрафов по i-й строке и j-му столбцу.

Если план транспортной задачи является оптимальным, то ему соответствует система из m+n чисел Ui и Vj, удовлетворяющих условиям: Ui+Vj=Cij для занятых клеток и Ui+Vj≤Сij в свободных клетках. Числа Ui и Vj называются потенциалами соответственно поставщиков и потребителей. При решении одному неизвестному потенциалу придается произвольное значение. [3 c.141]

Дата добавления: 2017-01-13