Фрагменты теории

УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАНИЯ

ЦЕЛЬ И СОДЕРЖАНИЕ ЗАДАНИЯ

ВВЕДЕНИЕ

М 74

Рецензенты:

В.В. Смагин – канд.тех. наук, доцент кафедры НГ, и и КГ

В.М. Бабенко – доцент кафедры НГ, и и КГ

О.В. Мухина - доцент кафедры НГ, и и КГ

Составители: А.Ф. Медведь¹, В.Г. Середа²

М 74 Моделирование сечений, пересечений и разверток поверхностей: метод. указания / сост. А.Ф. Медведь¹, В.Г. Середа². – Севастополь: СевГУ, 2016. – 28 с.: ил.

Методические указания составлены в соответствии с рабочей программой дисциплины «Начертательная геометрия и инженерная графика» на основании государственного образовательного стандарта высшего профессионального образования.

В указаниях даны варианты индивидуальных заданий, изложена методика графических построений и приведены образцы выполненных заданий.

Методические указания предназначены для студентов технических специальностей дневной и заочной формы обучения.

Рекомендовано учебно-методическим советом института в качестве методических указаний.

.

УДК 514.18(076)

© Медведь А.Ф.¹,

Середа В.Г.², сост., 2016

© ФГАОУВО «Севастопольский

государственный университет», 2016

СОДЕРЖАНИЕ

ВВЕДЕНИЕ
1. Цель и содержание задания
2. Указания к выполнению задания
3. Фрагменты теории
4. Пошаговое выполнение задач
4.1. Решение задачи 1
4.2. Решение задачи 2
4.3. Решение задачи 3
4.4. Перенос точки с развертки на поверхность
5. Вопросы для самоконтроля
ЗАКЛЮЧЕНИЕ
БИБЛИОГРАФИЧЕСКИЙ СПИСОК ЛИТЕРАТУРЫ

В инженерной практике встречаются задачи, в которых необходимо построить проекции поверхностей, усеченных плоскостями, выполнить построения линий пересечения поверхностей, а также построить развертку (плоскую фигуру, полученную после совмещения поверхности с плоскостью) поверхности.

Сечение – это плоская фигура, ограниченная линией пересечения плоскости с поверхностью.

Сечение многогранника – плоский многоугольник с числом вершин равным числу пересеченных плоскостью ребер.

Сечение кривой поверхности – плоская фигура, ограниченная кривой линией.

Линией пересечения двух кривых поверхностей является пространственная кривая.

Развертка поверхности – это плоская фигура, полученная после совмещения поверхности с плоскостью путем изгиба.

Вариант для выполнения задания определяется как остаток от деления трех последних цифр номера зачетной книжки на 30. Например, если номер зачетной книжки студента 030231, то он выполняет 21-й вариант, так как при делении 231 на 30 в остатке будет 21. Если остаток равен нулю, то принимается 30 вариант.

Цель задания – приобретение студентами практических навыков построений на чертеже сечений поверхностей плоскостью, линий пересечения поверхностей и их разверток.

Содержание работы. Задание состоит из трех задач.

Задача 1. Построить три проекции пирамиды, усеченной плоскостями.

Задача 2. Построить две проекции линии пересечения конуса со сферой (нечетные варианты – способом секущих плоскостей, а четные – способом концентрических сфер).

Задача 3. Построить развертку усеченной пирамиды, приведенной в задаче 1.

Задание выполняется на одном листе формата А3 (420х297). Образец выполненного задания приведен на рис. 1.

Решение задачи 1 выполняется вверху на левой половине листа, решение задачи 2 – на правой половине листа, а решение задачи 3 – внизу на левой половине листа. Рекомендуемая компоновка листа приведена на рисунке 2.

Исходные данные к задачам 1 и 2 выбираются по таблицам 1 и 2, а для задачи 3 из задачи 2. Чертежи поверхностей выполняются в масштабе 1:1.

Задание выполняется в следующей последовательности.

1. Выбираем по варианту из таблицы 1 поверхность пирамиды и параметры, характеризующие положение секущих плоскостей, а из таблицы 2 параметры пересекающихся поверхностей – конуса и сферы.

2. Строим в тонких линиях (толщина 0,2…0,3 мм) три проекции пирамиды в верхней части листа слева.

3. Наносим положение секущих плоскостей на фронтальной проекции пирамиды.

4. Достраиваем горизонтальную и профильную проекции секущих плоскостей.

5. Строим развертку усеченной пирамиды в нижней части листа.

6. Строим в тонких линиях две проекции пересекающихся геометрических тел.

7. Строим линию пересечения геометрических тел.

8. Обводим толстой линией (толщина 0,7…0,8 мм) контурные линии.

9. Заполняем основную надпись.

Рис. 1

Таблица 1 – Исходные данные к задаче 1

№ варианта	Параметры, мм	Поверхность пирамиды
d	h	a	b	c	e

Таблица 2 – Исходные данные к задаче 2

№ варианта	Параметры, мм	Поверхности конуса и сферы
H	R	r	a	b

Рис. 2

Сечение пирамиды плоскостью – это плоский многоугольник, число вершин которого равно числу пересеченных ребер. Сечение геометрических тел плоскостями строится по алгоритму, содержащему следующие операции:

– определить расположение поверхности и секущих плоскостей относительно друг друга и плоскостей проекций;

– определить количество секущих плоскостей;

– построить проекции опорных и промежуточных точек линии контура сечения на каждом участке;

– определить проекции линии контура сечения, соединяя соответствующие опорные и промежуточные точки.

К опорным точкам относятся: экстремальные точки (высшая и низшая, самая близкая и самая удаленная, крайняя левая и крайняя правая) и точки видимости (точки, разграничивающие линию сечения на видимую и невидимую части). Видимыми будут проекции тех точек линии контура сечения, которые принадлежат видимым на этой проекции граням, ребрам или образующим поверхности.

Следует помнить, что если секущая плоскость частного положения, то одна проекция контура сечения многогранника прямая, а другая – многоугольник.

При пересечении двух криволинейных поверхностей образуется пространственная кривая линия, порядок которой определяется произведением порядков пересекающихся поверхностей.

Для построения линии пересечения двух поверхностей вращения в задании рекомендуется использовать два способа:

– способ секущих плоскостей;

– способ секущих концентрических сфер.

Способ секущих плоскостей применяется, если обе поверхности можно пересечь плоскостями уровня по простейшим линиям (прямым или окружностям).

Способ секущих концентрических сфер применяется при соблюдении следующих условий:

– если пересекаются поверхности вращения;

– если пересекаются оси этих поверхностей;

– если пересекающиеся оси образуют плоскость уровня.

Решение задач на построение линии пересечения двух поверхностей выполняется по общему алгоритму, состоящему из следующих операций:

– построить поверхность-посредник, пересекающий заданные поверхности по прямым или окружностям;

– построить линии пересечения поверхности-посредника с каждой из заданных поверхностей;

– построить точки пересечения полученных линий;

– выполнить три предыдущие графические операции для получения необходимого числа опорных (определяющих конфигурацию и видимость участков линии пересечения) и промежуточных (уточняющих конфигурацию линии пересечения) точек линии пересечения;

– построить проекции линии пересечения поверхностей, проходящей через полученные опорные и промежуточные точки, с учетом ее видимости (видимы те точки линии пересечения, которые принадлежат двум видимым образующим).

Центр сфер-посредников находится в точке пересечения осей вращения поверхностей. Область существования сфер-посредников определяется сферическим кольцом. Максимальный радиус R_max кольца равен расстоянию от центра сферы до наиболее удаленной точки пересечения очерков поверхностей. Минимальный радиус R_min кольца равен расстоянию от центра сферы до точки касания очерка поверхности большего размера.

Развертывание поверхностей – это задачи, в которых по заданным проекциям поверхности определяются совмещенные с плоскостью истинные величины ее отсеков.

Решение этих задач основано на знании следующих свойств развертываемых поверхностей:

– длины двух соответствующих линий поверхности и развертки равны между собой;

– углы между соответствующими линиями поверхности и развертки равны между собой;

– замкнутая линия на поверхности и соответствующая ей линия на развертке ограничивают равные площади;

– прямой на поверхности соответствует прямая линия на развертке, (но не наоборот);

– параллельным прямым на поверхности соответствуют параллельные прямые на развертке.

Встречающиеся в задании пошаговое деление окружности на пять равных частей приведено в таблице 3. Деление окружности на шесть частей понятно из табл. 4.

Наиболее часто встречающиеся графические операции в задании приведены в табл. 5.

Таблица 3 – Деление окружности на пять равных частей

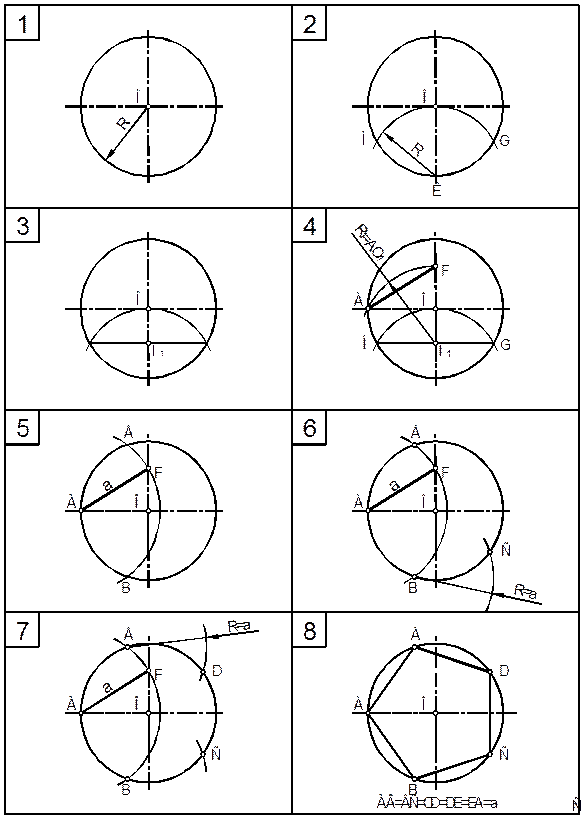
Таблица 4 – Деление окружности на шесть равных частей

Таблица 5 – Основные графические операции, встречающиеся в индивидуальных заданиях

Если секущая плоскость параллельна горизонтальной плоскости проекций, то сечение шестигранной пирамиды шестиугольник, подобный основанию. Инвариант. Если точка лежит на поверхности, то она лежит на линии принадлежащей этой поверхности. Алгоритм. 1. Строим фронтальную проекцию Г2 вспомогательной плоскости уровня G, проходящей через заданную проекцию А3 точки А на поверхности. Плоскость G пересекает пирамиду по шестиугольнику m. Фронтальная проекция шестиугольника m2 совпадает с фронтальной проекцией Г2 секущей плоскости G. 2. Строим горизонтальную проекцию m1 линии пересечения m. 3. Проводим линию связи из точки А2 до пересечения с горизонтальной проекцией шестиугольника m1 в точке А1.

Сечение пирамиды горизонтальной плоскостью Г.

Продолжение табл. 5

Сечение конуса горизонтальной плоскостью Г.

Если секущая плоскость параллельна горизонтальной плоскости проекций, то сечение конуса – окружность. Алгоритм. 1. Строим фронтальную проекцию Г2 вспомогательной плоскости уровня G, проходящей через заданную точку А. Плоскость G пересекает конус по окружности m радиусом R. Фронтальная проекция m2 окружности совпадает с фронтальной проекцией Г2 плоскости G. 2. Строим горизонтальную проекцию m1 окружности радиусом R. 3. Строим горизонтальную проекцию А1 точки А, как результат пересечения вертикальной линии связи с m1.

Сечение конуса фронтально проецирующей плоскостью Т, параллельной образующей конуса.

Если секущая плоскость параллельна одной образующей, то сечение конуса – парабола. Алгоритм. 1. Разбиваем фронтальную проекцию линии сечения на ряд опорных A2, B2, C2 и промежуточных точек, F2, E2, D2. 2. Строим горизонтальные проекции опорных точек А, В и С, как точек, принадлежащих окружностям на поверхности конуса. 3. Строим горизонтальные проекции промежуточных точек F, E и D (например, точка лежит на окружности m с радиусом R).

Продолжение табл. 5

Если секущая плоскость пересекает образующие конуса и не перпендикулярна оси вращения, то сечение конуса – эллипс. Алгоритм. 1. Определяем на фронтальной проекции размер большой оси A2B2 эллипса. Малая ось эллипса проходит через середину (точка С) большой оси АВ эллипса. 2. Строим горизонтальную проекцию А1В1 и C1D1 осей эллипса. Точки А1 и В1 лежат на горизонтальных проекциях очерковых образующих конуса. Точки C1 и D1 лежат на горизонтальной проекции окружности, лежащей в плоскости уровня Г, проходящей через точки С и D. 3. Выбираем на фронтальной проекции промежуточные точки Е2 и F2, принадлежащие эллипсу. 4. Строим горизонтальные проекции Е1 и F1 промежуточных точек Е и F. 5. Соединяем полученные точки лекальной кривой линией.

Сечение конуса фронтально проецирующей плоскостью Т.

Если секущая плоскость параллельна оси конуса, то сечение конуса – гипербола. Алгоритм. 1. Определяем точки A и B основания гиперболы, как результат пересечения плоскости S с основанием конуса. 2. Определяем вершину C гиперболы, лежащую на окружности, принадлежащей конусу и касающейся плоскости S. Точка касания является основанием перпендикуляра, опущенного из оси конуса на плоскость. 3. Достраиваем проекции промежуточных точек, как точек лежащих на окружностях принадлежащих конусу в местах пересечения с секущей плоскостью S.

Сечение конуса фронтальной плоскостью

Продолжение табл. 5

Определение общих точек пересечения повехностей способом секущих плоскостей.

Алгоритм. 1. Строим фронтальную проекцию G2 вспомогательной секущей плоскости Г. 2. Строим горизонтальные проекции m1 и n1 окружностей m и n, как результат пересечения горизонтальной секущей плоскости c двумя поверхностями. 3. Определяем точки D1 и D1¢ пересечения окружностей m1 и n1, которые принадлежат линии пересечения поверхностей. 4. Строим фронтальные проекции D2 и D2¢ точек D и D¢. Точка D2¢ – невидимая и на фронтальной проекции не обозначена.

Определение общих точек пересечения повехностей способом секущих концентрических сфер.

Алгоритм. 1. Определяем фронтальную проекцию О2 центра О вспомогательных секущих сфер, как результат пересечении осей поверхностей вращения (конуса и сферы). 2. Строим фронтальную проекцию вспомогательной секущей сферы радиусом Rc, которая пересекает коническую поверхность по двум окружностям m и k, а сферу по окружности n. 3. Определяем фронтальные проекции С2 и D2, точек С и D, как результат пересечения окружностей m2 c n2 и k2 c n2 соответственно. 4. Строим горизонтальные проекции окружностей m1 и k1. 5. Определяем горизонтальные проекции С1 и D1 точек С и D, как результат пересечения вертикальных линий связи с соответствующими окружностями m1 и k1.

Дата добавления: 2017-01-13