
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вопросы для контроля. Задачи, решаемые на картах и планах
|
|
|
|
А В
Задачи, решаемые на картах и планах
На картах и планах решаются задачи определения прямоугольных и географических координат, измерение расстояний, углов ориентирования, уклонов и углов наклона, решение обратных геодезических задач и другие. Остановимся на рассмотрении некоторых из них.
а). Измерение на карте углов ориентирования
Ориентировать линию на местности – значит определить её положение относительно другого направления, принятого за исходное.
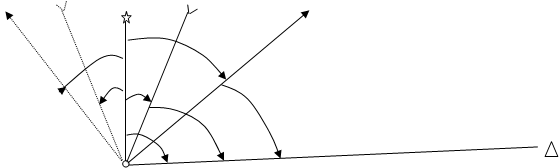
В качестве исходных в геодезии используют следующие направления (рисунок 11):
- северное направление истинного меридиана;
- северное направление осевого меридиана Х 0;
- северное направление магнитного меридиана;
Углы ориентирования, измеряемые относительно перечисленных исходных направлений называют соответственно истинным азимутом Аи, дирекционным углом  , магнитным азимутом Ам. Все эти углы измеряются по ходу часовой стрелки от 0 0 до 360 0.
, магнитным азимутом Ам. Все эти углы измеряются по ходу часовой стрелки от 0 0 до 360 0.
Ист. мерид.Линия сетки Магнитн. мерид.
-  +
+ 
-  +
+ 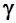
Аи  А м
А м
Рисунок 11 - Углы ориентирования
Угол 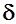 (между истинным и магнитным меридианами называется магнитным склонением. Оно может быть западным - склонение со знаком " - " (-
(между истинным и магнитным меридианами называется магнитным склонением. Оно может быть западным - склонение со знаком " - " (- 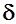 ) или восточным - склонение со знаком " + " (+
) или восточным - склонение со знаком " + " (+ 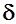 ).
).
Угол 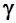 между истинным меридианом и вертикальной линией сетки называют сближением меридианов. Оно так, же как и магнитное склонение может быть западным - (-
между истинным меридианом и вертикальной линией сетки называют сближением меридианов. Оно так, же как и магнитное склонение может быть западным - (- 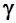 ) или восточным (+
) или восточным (+ 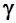 ).
).
Значения магнитного склонения и сближения меридианов подписываются под южной рамкой карты. При необходимости сближение меридианов нов может быть вычислено по формуле
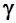 = sin
= sin 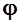 (
( -
-  0),
0),
где 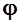 ,
,  - географические соответственно широта и долгота точки;
- географические соответственно широта и долгота точки;
 0 - долгота осевого меридиана зоны;
0 - долгота осевого меридиана зоны;
Между истинным, магнитным азимутами и дирекционным углом существует определённая математическая зависимость.
Из рисунка 11 нетрудно заметить, что
А и =  + (
+ (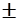
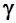 ),
),
А и = А м + (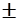
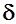 ).
).
Приравняв правые части равенства, получим
А м =  + (
+ (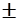
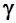 ) - (±
) - (± 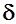 ).
).
 Направления могут быть прямыми и обратными. У линии АВ (рисунок 12) направление с точки А на точку В называют прямым, а с точки В к на точку А – обратным.
Направления могут быть прямыми и обратными. У линии АВ (рисунок 12) направление с точки А на точку В называют прямым, а с точки В к на точку А – обратным.
 АВ В
АВ В
А  ВА
ВА
Рисунок 12 - Прямые и обратные направления
(дирекционные углы, азимуты направлений)
Соответственно и дирекционные углы и азимуты направлений бывают прямыми и обратными:  АВ – прямой дирекционный угол (
АВ – прямой дирекционный угол ( пр),
пр),  ВА – обратный дирекционный угол (
ВА – обратный дирекционный угол ( обр),
обр),
Зависимость между прямым и обратным дирекционными углами выражается соотношением
 пр =
пр =  обр ± 180 0.
обр ± 180 0.
На практике при решении различных задач часто используются не дирекционные углы, а румбы.
Румбом направления r называют острый угол в пределах 900 в одной из четвертей между ближайшим северным или южным меридианом (вертикальной линией сетки) и данным направлением.
При обозначение румба указывают четверть, а затем угловую величину в градусной мере. Например, для первой четверти - СВ: 450 35 ', для второй - ЮВ: 650 37 '; для третьей ЮЗ: 420 35 ' ; для четвёртой - СЗ: 570 51 '
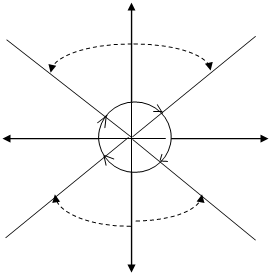
Румбы и дирекционные углы (азимуты) направлений могут быть представлены в виде рисунка 13.
С
 |
r1V r1
 1
1
 1V
1V
З 1V 1 В
111  11 11
11 11
 111
111
r111 r11
Ю
Рисунок 13 - Зависимость между румбом и дирекционным углом
Из приведенного рисунка нетрудно вывести и соотношения, представляющие собой зависимость между дирекционным углом (азимутом) направления и румбом (таблица 1).
Таблица 1 - Соотношения между румбами и дирекционными углами
| Знаки | Четверть | Формулы | |
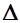 Х Х
| 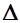 У У
| ||
| + | + | 1 - СВ |  1 = r1 1 = r1
|
| - | + | 11 - ЮВ |  11 = 180 0 - r11 11 = 180 0 - r11
|
| - | - | 111 - ЮЗ |  11 = 180 0 + r111 11 = 180 0 + r111
|
| + | - | 1V - CЗ |  11 = 360 0 - r1V 11 = 360 0 - r1V
|
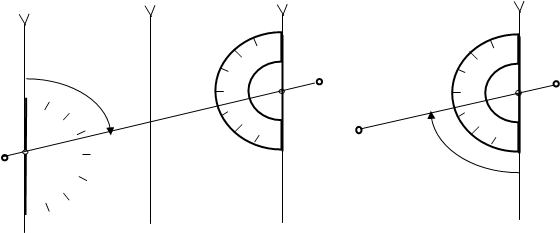
Значения дирекционных углов и румбов измеряются по карте, если провести в данной точке исходное направление. Дирекционные углы измеряются с помощью транспортира, устанавливаемого в точке пересечения данного направления с вертикальной линией сетки или линией ей параллельной, относительно северного направления вертикальной линии сетки от 00 до 3600, а румбы – от 00 до 900 относительно северного или южного направлений вертикальной линии сетки. На рисунке 14 а,б показаны примеры измерения по карте дирекционного угла и румба.
а) Измерение дирекционного угла б) Измерение румба
В

 АВ В
АВ В
 ВА А r ВА
ВА А r ВА
А
Рисунок 14 - Измерения по карте дирекционного угла и румба
б) Решение обратной геодезической задачи
Сущность решения задачи заключается в определении по прямоугольным координатам двух точек расстояния между ними и дирекционного угла направления с одной точки на другую (рисунок 15).
Х
 | |||
 | |||
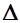 У
У
В
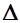 Х
Х  АВ d AB
АВ d AB 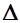 Х
Х
 |
А У
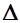 У
У
Рисунок 15 - Решение обратной геодезической задачи
Из треугольника АВС d2 АВ = 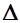 Х2 +
Х2 + 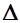 У2. Из этого же треугольника следует, что если направление находится в первой четверти, то дирекционный угол (АВ вычисляется из соотношения
У2. Из этого же треугольника следует, что если направление находится в первой четверти, то дирекционный угол (АВ вычисляется из соотношения
 АВ = arc tg (±
АВ = arc tg (± 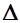 У) / (± (
У) / (± (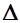 Х).
Х).
В общем случае для нахождения дирекционного угла направления необходимо определить румб направления по аналогичной формуле
rАВ = arc tg (± 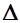 У) / (±
У) / (± 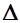 Х),
Х),
затем по знакам 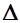 У и
У и 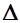 Х определить четверть, в которой находится направление, после чего перейти к дирекционному углу по соответствующей формуле таблицы 1.
Х определить четверть, в которой находится направление, после чего перейти к дирекционному углу по соответствующей формуле таблицы 1.
Вычислив румб r и дирекционный угол  направления, расстояние d между двумя точками можно вычислить по формулам
направления, расстояние d между двумя точками можно вычислить по формулам



 d =
d = 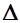 У / sin r =
У / sin r = 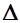 Х / cos r,
Х / cos r,
d = (± 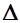 У) / sin
У) / sin  = (±
= (± 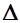 Х) / cos
Х) / cos  .
.
в). Измерение площадей по карте
Аналитический способ. Его применяют в том случае, если участок местности ограничен ломаной линией, а прямоугольные координаты вершин известны.
Принцип определения площади участка местности, показанного на рисунке 16, заключается в следующем:
- вершины участка проектируют на оси Х и У, в результате чего образуется ряд трапеций, основаниями которых являются координаты Хi вершин участков, а высотами – приращения координат 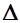 Уi;
Уi;
- вычисляют площади трапеций и получают площадь участка, как сумму площадей трапеций.
 Х
Х
ХВ B
ХА A
ХС C
А ' B ' С '
0 УА УВ УС
Рисунок 16 - Аналитический способ определения площади
Рассмотрим в качестве примера определение площади участка местности, образованного треугольником АВС, координаты вершин которого ХА, УА; ХВ, УВ; ХС, УС.
Итак, необходимо определить площади трёх трапеций: АА'ВВ', ВВ'СС', АА'СС'.
Площади указанных трапеций определяются по формулам
S1 = S АА'ВВ' = 0.5 (ХА + ХВ) (УВ – УА),
S2 = S DD'CC' = 0.5 (ХB + ХC) (УC – УB),
S3 = S АА'CC' = 0.5 (ХА + ХC) (УC – УА).
Площадь S треугольника АВС может быть вычислена по формуле
S = S1 + S2 + S3.
Сложив выражения для определения площадей и выполнив несложные преобразования, получим
S = 0.5 ХА (УВ – УС)+ ХВ (УС – УА) + ХС (УА – УВ)
или
S = 0.5 УА (ХС – ХВ)+ УВ (ХА – ХС) + УС (ХВ – ХА).
Если вершины участка пронумеровать по часовой стрелке, то формулы определения площади можно представить в следующем обобщённом виде:
S = 0.5 Хi (У i+1 - У i-1),
S = 0.5 Уi (Х i-1 - Х i+1),
где i = 1, 2, 3..., n.
Механический способ. Он основан на использовании специального прибора – полярного планиметра (рисунок 17).
Рисунок 17 - Полярный планиметр
Данный планиметр имеет два рычага - полюсный 1 и обводной 2, соединённых шаровым шарниром 3, укреплённым на конце полюсного рычага. На обводном рычаге помещена передвижная каретка 4 с отсчётным устройством 5. Обводной рычаг имеет на конце ручку 6 и лупу 7 с кружком в центре (в первых образцах планиметров вместо лупы на конце обводного рычага закреплена игла)
Перед измерением площади центр лупы устанавливают над какой-то точкой контура, принятой за начальную и по отсчётному механизму делают отсчёт u1. Затем обводят измеряемую площадь и снимают отсчёт u2 после установки центра лупы вновь над начальной точкой.
В принципе искомая площадь вычисляется по формуле
S = C (U2 – U1),
где С – цена одного деления планиметра.
Величина С определяется несколькими обводами контура геометрической фигуры известной площади. В качестве неё выбирают, как правило, контур одного или нескольких квадратов километровой сетки.
Для обеспечения достаточной точности площадь вычисляют по результатам нескольких обводов участка карты или плана.
Точность определения площади обоими способами неодинакова. Наибольшей точностью (1:1000) характеризуется аналитический способ. Механический способ позволяет определить площадь с относительной ошибкой 1:200 - 1:300.
1. Понятие плана и карты.
2. Виды масштабов, точность масштаба.
3. Понятие номенклатуры карт и планов. Как получают лист карты масштаба 1:1000000.
4. Понятие горизонтали. Как получают изображение горизонтали на плоскости.
5. Понятие высоты сечения, заложения.
6. Понятие уклона, крутизна ската. Выразить уклон i = 0.053 в процентах и промиле.
7. Понятие дирекционного угла, истинного, магнитного азимутов Зависимость между ними.
8. Понятие румба. Зависимость между румбом и дирекционным углом.
9. Сущность решение обратной геодезической задачи.
10. Сущность аналитического способа определения площади.
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 272; Нарушение авторских прав?; Мы поможем в написании вашей работы!