Равносильность формул логики предикатов

Пусть формулы А и В имеют одно и то же множество свободных переменных.

Определение. Формулы А и В равносильны в данной интерпретации, если на любом наборе значений свободных переменных они принимают одинаковые значения (т. е. если формулы выражают в данной интерпретации один и тот же предикат).

Определение. Формулы А и В равносильны на множестве М, если они равносильны во всех интерпретациях, заданных на множестве М..

Определение. Формулы А и В равносильны в логике предикатов, если они равносильны на всех множествах (АºВ).

Укажем несколько правил перехода от одних формул к другим, им равносильным.

Для формул логики предикатов сохраняются все равносильности и правила равносильных преобразований логики высказываний.

Утверждение. Всякую формулу логики предикатов, содержащую символы ® и», можно преобразовать в равносильную ей формулу, не содержащую этих символов.

Кроме этого, существуют следующие правила:

1. Перенос квантора через отрицание

2. Вынос квантора за скобки

3. Перестановка одноименных кванторов

"х "у А(х, у) º "у "х А(х, у),

$х $у А(х, у) º $у $х А(х, у).

4. Переименование связанных переменных.

Заменяя связанную переменную формулы А другой переменной, не входящей в эту формулу, в кванторе и всюду в области действия квантора получаем формулу, равносильную А.

Определение. Формула А, равносильная формуле В, и не содержащая символов ®,», а также составных формул под знаком отрицания, называется приведенной формой формулы В.

Теорема. Для любой формулы существует равносильная ей приведенная формула, причем множества свободных и связанных переменных этих формул совпадают.

Пример.

Преобразовать в приведенную форму формулу .

Решение.

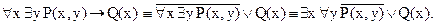
Дата добавления: 2017-01-13