Методические указания к решению задачи 3

Для решения этой задачи требуются знания закона Ома для участка цепи, законов Кирхгофа и методик расчета сложных электрических цепей постоянного тока.

Содержание зада­чи и схема цепи с соответствующими данными приведены в индивидуальном задании. Перед решением задачи рассмотрите типовой пример 3.

Пример3а

Рис. 1.3а. Схема сложной электрической цепи постоянного тока

В качестве примера рассмотрим цепь, схема которой изображена на рис. 3а.

Схема содержит пять ветвей (m =5) и три узла (n =3). На схеме обозначаем произвольно направление токов в ветвях и направления обхода контуров (против часовой стрелки). При расчете данной цепи по методу непосредственного применения законов Кирхгофа необходимо решать систему из пяти уравнений.

Дано: Е₁=Е₂=30 В;

R₁= R₂=1Ом,

R₃= 4Ом,

R₄= 2Ом,

R₅= 3Ом.

Определить токи в ветвях: I₁, I₂, I₃, I₄,I₅

По первому закону Кирхгофа составляем два уравнения для двух любых узлов из трех.

Для узла 2: I₁- I₃ – I₅=0 (3.1)

Для узла 3: - + I₅=0 (3.2)

Остальные недостающие уравнения составляем по второму закону Кирхгофа.

Для контура I: Е₁= I₁R₁+ I₃R₃ (3.3)

II: Е₂ = I₂R₂+ I₄R₄ (3.4)

III: 0 = I₃R₃ + I₄R₄ – I₅R₅ (3.5)

С целью упрощения расчета сокращаем число уравнений системы до двух, используя метод подстановок (метод Гаусса).

Из уравнения для второго узла находим ток I₁ = I₃ +I₅ и подставляем его в уравнение для первого контура и получаем:

Е₁= (I₃+ I₅) R₁+ I₃R₃= I₃(R₃+ R₁) + I₅R₁ (3.6)

Из уравнения для третьего узла находим ток I₂ = I₄ +I₅ и подставляем его в уравнение для второго контура и получаем:

Е₂ = (I₄ +I₅)R ₂+ I₄R₄+= I₄(R ₂+ R₄) +I₅R ₂ (3.7)

Из уравнения для третьего контура находим ток I₅:

I₅= (3.8)

Подставляем значение тока I₅ из уравнения (3.8) в уравнения (3.6) и (3.7).

В результате получаем:

Е₁= I₃(R₃+ R₁+ R₃ R₁/ R₅) + I₄(R₄ R₁/ R₅)

Е₂= I₃(R₂ R₃/ R₅)+ I₄(R₂+ R₄+ R₂ R₄/ R₅)

Подставив в систему из двух уравнений числовые значения э.д.с. и сопротивлений получим:

19/3 I₃ + 2/3 I₄=30

4/3 I₃ +11/3 I₄=30

Рассмотрим решение системы уравнений с помощью определителей:

I₃= I₄= ,

где -главный определитель системы уравнения;

_I3 - частный определитель по току I₃;

_I4 - частный определитель по току I₄.

Главный определитель содержит столбцы левой части системы уравнений; - частный определитель получают путем замены столбца левой части, где находится неизвестный ток, столбцом правой части системы уравнений:

19/3 2/3 30 2/3 19/3 30

= _I3 = _I4 =

4/3 11/3 30 11/3 4/3 30

= 19/3∙11/3 - 4/3∙2/3 =22∙1/3

_I3=30∙11/3 -30∙2/3 =90

_I4 =19/3∙30 - 4/3∙30 =150.

Ток в третий ветви I₃= =90/ 22∙1/3 = 4,03А.

Ток в четвертой ветви I₄= = 150/22∙1/3 = 6,72 А.

Из уравнения (3.8) ток в пятой ветви

I₅= = 9,85А

Из уравнения (3.1) ток в первой ветви

I₁= I₃+ I₅= 4,03 +9,85= 13,88А, а из уравнения (3.2) ток во второй ветви

I₂= I₄+ I₅= 6,72+9,85=16,57А

Правильность расчета токов в ветвях электрической цепи проверяем с помощью уравнения баланса мощностей источников и приемников электроэнергии:

Правая часть характеризует мощность пассивных источников, а левая – мощность активных элементов ^цепи. При составлении уравнения баланса мощностей следует иметь в виду, что в левой части его со знаком плюс записываются те слагаемые, для которых направления э.д.с. и тока совпадают, если не совпадают, то со знаком минус.

Баланс мощностей соответствует следующему уравнению:

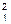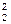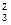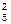Е₁ I₁+ Е₂ I₂= I R₁+ I R₂+ I R₃+ I R₄+ I R₅$

30∙13,88+30∙16,57= 13,88²∙1+16,57²∙1+ 4,03²∙4+6,72²∙2+9,85²∙3

914 Вт = 914 Вт.

Соблюдение баланса мощностей свидетельствует о правильности расчета токов в электрической цепи.

Пример 3б.

Для расчета сложных электрических цепей можно использовать метод контурных токов, в основу которого положены расчетные контурные токи, замыкающиеся по смежным контурам разветвленных электрических цепей.

В процессе расчета по этому методу определяют независимые замкнутые контуры и задаются условными положительными направлениями контурных токов. Число уравнений равно числу контурных токов. Направления обхода контуров выбирают совпадающими с направлениями контурных токов.

При составлении уравнений по второму закону Кирхгофа для контуров э.д.с. источников и напряжения принимаются положительными, если их направление совпадает с направлением контурных токов, при несовпадении – со знаком минус.

Величины контурных токов во внешних ветвях равны по значению токам в них. Токи в смежных ветвях равны разности контурных токов соседних контуров.

Знак контурных токов зависит от того, совпадает направление контурного тока с током в данной ветви или нет.

Определить токи в ветвях методом контурных токов для той же электрической цепи (рис. 1.3а).

По второму закону Кирхгофа составляем три уравнения электрического состояния: для верхнего, среднего и нижнего контуров:

I_I (R₁+R₃) + I_IIR₁=E₁

I_II (R₁+R₂ +R₅) + I_I R₁+ I_III R₂= E₁+ E₂

I_II R₂ ++ I_III (R₂ + R₄)= E₂

Подставляя в полученные уравнения известные величины, имеем:

5 I_I + I_II = 30

I_I+ 5 I_II + I_III = 60

I_II + 3I_III = 30

Главный определитель системы:

5 1 0 5 1 1 1 1 5

= 1 5 1= 5 1 3 - 1 0 3 + 0 0 1 = 5 (15 – 1) – (3 – 0) = 70 – 3 =67

0 1 3

Определитель по току I_I:

30 1 0 5 1 60 1 60 5

= 60 5 1 = 30 1 3 - 1 30 3 + 0 30 1 = 30(15 -1) – (180 -30)

30 1 3

= 420 -150 = 270.

Определитель по току I_II:

5 30 0 60 1 1 1 1 60

= 1 60 1 = 5 30 3 - 30 0 3 + 0 0 30

0 30 3

= 5(180 – 30) - 30(3 -0) = 660.

Определитель по току I_III:

5 1 30 5 60 1 60 1 5

= 1 5 60 = 5 1 30 - 1 0 30 + 30 0 1

0 1 30

= 5 (150 – 60) - 30 + 30 (1 - 0) = 450.

Вычисляем контурные токи:

I_III =

Токи в ветвях электрической цепи определяем с учетом первого закона Кирхгофа для узловых точек:

I₁= I_I +I_II= 4,03 + 9,85 = 13,88А;

I₂ = I_II + I_III = 9,85 + 6,72 = 16, 57А;

I₃= I_I= 4,03A; I₄ = I_III =6,72 A; I₅ = I_II= 9,85 A.

Ответ: I₁=13,88А; I₂ =16, 57А; I₃=4,03A; I₄ = 6,72 A; I₅ = 9,85 A.

Пример 3в.

Для цепи рис. 1.3б определить токи во всех участках и напряжения между узловыми точками А, Би Впри следующих данных: R₁=R₃=2 Ом; R₂=1,6 Ом; E₁ = 3,6 В; E₂ = 4,8 В; R_ВТ1 = R_ВТ2 = 0,5 Ом.

Решение задачи

1. Применение метода наложения к цепи рис. 3б.

Разветвленные цепи с несколькими-источниками

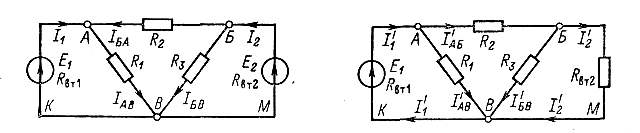
Рис. 1.3.б. Сложная цепь с двумя Рис. 1.3.в. Исключение одной ЭДС
источниками энергии из сложной цепи

Рис. 1.3г. Исключение второй ЭДС из сложной цепи

По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частичных токов, созданных каждой э.д.с. в отдельности.

2. Обозначение частичных токов.

Все частичные токи от э.д.с. Е₁ обозначим буквой I с одним штрихом, а от э.д.с. Е₂ – с двумя штрихами.

3. Вычисление частичных токов.

Для цепи с э.д.с. Е₁ (рис.3.в) рассчитаем сначала общее сопротивление.

Сопротивление участка БВ

но соединено последовательно с сопротивлением R ₂, поэтому

Два одинаковых сопротивления Raбв и R₁ соединены параллельно, поэтому общее сопротивление всей внешней цепи

Ток источника

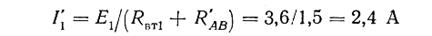
разветвляется в узловой точке А на два одинаковых тока:

Ток I^' _АБ разветвляется в узловой точке Б на токи

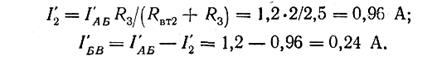
Рис. 1.3д. Исключение второй ЭДС из сложной цепи

Для цепи с ЭДС Е₂ (рис. 3г)

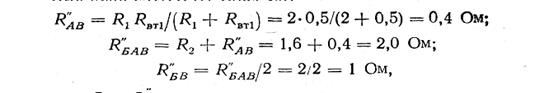
так как Rз=R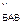

В ветви источника с э.д.с. Е₂ ток

Поскольку R"_бав = R з=2,0 Ом, ток

Токи в параллельных ветвях участка АВ

5. Вычисление токов в исходной цепи (рис. 3б).

Выполним алгебраическое сложение частич­ных токов.

На участке ВКА частичный ток (рис, 3в) направлен

от узла В к узлу А, а частичный ток (рис. 3г) — от узла А к узлу В, т. е. навстречу первому. Поэтому суммар­ный ток

Направление тока I₁ (рис. 3б) совпадает с направлени­ем большего частичного тока, т. е. тока . Аналогичным образом определяем I_Ба и I₂:

Направления токов I_БА и I₂ (рис. 3б) совпадают с на­правлениями токов I"_БА и I2 соответственно.

В ветви АВ оба частичных тока (I" _АВ и Г _АВ)совпадают по направлению, поэтому

Аналогично

6. Вычисление напряжений.

Напряжения меж­ду узловыми точками

7. Проверка результатов вычислений.

Для проверки расчетов составим уравнения по законам Кирхгофа.

Для узла А, I_АВ=I₁ + I_БА; действительно 1,52 = 1,12+ 0,4.

Для узла Б, I₂=I_БА + I_БВ; действительно 2,24=0,4+1,84.

Для контура АБВ U ав— U вб+ U ба = 0, действительно +3,04—3,68+0,64 = 0

(обход против направления движе­ния стрелки часов).

Ответ: I₁=1,12 А; I₂ =2,24 А; I_БА =0,4 А; I_АВ =1,52 А; I_БВ =1,84 А; U_БА=0,64 В;

U_АВ=3,04 В; U_БВ= 3,68 В.

Дата добавления: 2017-01-13