Структура контрольной работы, рекомендации по выполнению заданий

Контрольная работа состоит из пяти практических заданий.

Задание 1. Найти предел

Чтобы вычислить предел, необходимо определить, чему равна функция в точке, соответствующей предельному значению аргумента.

В некоторых случаях задача не имеет конечного решения, а подстановка значения, к которому стремится переменная, дает неопределенность вида «ноль на ноль» или «бесконечность на бесконечность». В этом случае применимо правило, выведенное Бернулли и Лопиталем, которое подразумевает взятие первой производной.

Как и любое другое математическое понятие, предел может содержать под своим знаком выражение функции, слишком громоздкое или неудобное для простой подстановки. Тогда необходимо прежде упростить его, пользуясь обычными методами, например, группировка, вынесение общего множителя и замена переменной, при которой меняется и предельное значение аргумента.

Задание 2. Найти производную.

Для быстрого вычисления производных первым делом выучите таблицу производных основных элементарных функций.

Затем определите к какому типу относится ваша функция. Если это простая функция от одного переменного, найдите ее в таблице и вычислите.

Если вам нужно найти производную суммы или разности двух функций, то вычислите производные каждого слагаемого, а затем сложите их.

Вычисляйте производную произведения двух функций по формуле (f(x)×g(x))′=f(x)′×g(x)+f(x)×g(x)′, то есть как сумму произведений производной первой функции на вторую функцию и производной второй функции на первую функцию.

Если ваша функция представляет собой частное двух функций, то есть имеет вид f(x)/g(x), для вычисления ее производной используйте формулу (f(x)/g(x))′=(f(x)′×g(x)−f(x)×g(x)′)/(g(x)²).

Если вам нужно вычислить производную сложной функции, то есть функции имеющей вид f(g(x)), аргументом которой является какая-либо зависимость, используйте следующее правило: (f(g(x)))′=(f(g(x))′×(g(x))′. Сначала возьмите производную по сложному аргументу, считая его простым, затем посчитайте производную сложного аргумента и результаты перемножьте. Таким способом вы найдете производную любой степени вложенности. Например, (sin(x)³)′=3×(sin(x))²×(sin(x))′=3×(sin(x))²×cos(x).

Если ваша задача вычислить производную высшего порядка, то вычисляйте последовательно производные низшего порядка. Например, (x³)′′=((x³)′)′=(3×x²)′=6×x.

Задание 3. Исследовать функцию и построить график.

Найдите область определения функции. Например, функция sin(x) определена на всем интервале от -∞ до +∞, а функция 1/x — на интервале от -∞ до +∞ за исключением точки x = 0.

2 Определите области непрерывности и точки разрыва. Обычно функция непрерывна в той же самой области, где она определена. Чтобы обнаружить разрывы, нужно вычислить пределы функции при приближении аргумента к изолированным точкам внутри области определения. Например, функция 1/x стремится к бесконечности, когда x→0+, и к минус бесконечности, когда x→0-. Это значит, что в точке x = 0 она имеет разрыв второго рода. Если пределы в точке разрыва конечны, но не равны, то это разрыв первого рода. Если же они равны, то функция считается непрерывной, хотя в изолированной точке она и не определена.

3 Найдите вертикальные асимптоты, если они есть. Здесь вам помогут вычисления предыдущего шага, поскольку вертикальная асимптота практически всегда находится в точке разрыва второго рода. Однако иногда из области определения бывают исключены не отдельные точки, а целые интервалы точек, и тогда вертикальные асимптоты могут располагаться на краях этих интервалов.

4 Проверьте, обладает ли функция особыми свойствами: четностью, нечетностью и периодичностью. Функция будет четной, если для любого x в области определения f(x) = f(-x). Например, у= cos(x) и у=x²— четные функции.

5 Нечетность функции обозначает, что для любого x в области определения f(x) = -f(-x). Например, у=sin(x) и у=x³ — нечетные функции.

6 Периодичность — свойство, говорящее о том, что есть некое число T, называемое периодом, такое, что для любого x f(x) = f(x + T). Например, все основные тригонометрические функции (синус, косинус, тангенс) — периодические.

7 Найдите точки экстремума. Для этого вычислите производную от заданной функции и найдите те значения x, где она обращается в ноль. Например, функция f(x) = x³ + 9x² -15 имеет производную g(x) = 3x² + 18x, которая обращается в ноль при x = 0 и x = -6.

Чтобы определить, какие точки экстремума являются максимумами, а какие минимумами, отследите изменение знаков производной в найденных нулях. g(x) меняет знак с плюса на минус в точке x = -6, а в точке x = 0 обратно с минуса на плюс. Следовательно, функция f(x) в первой точке имеет максимум, а во второй — минимум.

9 Таким образом, вы нашли и области монотонности: f(x) монотонно возрастает на промежутке -∞;-6, монотонно убывает на -6;0 и снова возрастает на 0;+∞.

10 Найдите вторую производную. Ее корни покажут, где график заданной функции будет выпуклым, а где - вогнутым. Например, второй производной от функции f(x) будет h(x) = 6x + 18. Она обращается в ноль при x = -3, меняя при этом знак с минуса на плюс. Следовательно, график f(x) до этой точки будет выпуклым, после нее — вогнутым, а сама эта точка будет точкой перегиба.

11 У функции могут быть и другие асимптоты, кроме вертикальных, но только в том случае, если в ее область определения входит бесконечность. Чтобы их найти, вычислите предел f(x), когда x→∞ или x→-∞. Если он конечен, то вы нашли горизонтальную асимптоту.

12 Наклонная асимптота — прямая вида kx + b. Чтобы найти k, вычислите предел f(x)/x при x→∞. Чтобы найти b — предел (f(x) – kx) при том же x→∞.

13 Постройте график функции по вычисленным данным. Обозначьте асимптоты, если они есть. Отметьте точки экстремума и значения функции в них. Для большей точности графика вычислите значения функции еще в нескольких промежуточных точках. Исследование завершено.

Задание 4. Найти неопределенный интеграл.

Интегрирование - процесс, обратный дифференцированию. В большинстве учебников функция, получаемая в результате интегрирования, обозначается как F(x) и носит название первообразной. Производная первообразной равна F'(x)=f(x). Например, если в задаче дана функция f(x)=2x, процесс интегрирования выглядит следующим образом: ∫2x=x²+C, где C=const, при условии, что F'(x)=f(x)
Процесс интегрирования функции можно записать и иным образом:
∫f(x)=F(x)+C

2 Обязательно запомните следующие свойства интегралов:
1. Интеграл суммы равен сумме интегралов:
∫[f(x)+z(x)]=∫f(x)+∫z(x) Для доказательства этого свойства возьмите производные от левой и правой части интеграла, после чего используйте аналогичное свойство суммы производных, пройденное вами ранее.

2. Постоянный множитель выносится за знак интеграла: ∫AF(x)=A∫F(x), где A=const.

3 Простые интегралы вычисляются с использованием специальной таблицы. Однако, чаще всего в условиях задач встречаются сложные интегралы, для решения которых знания таблицы недостаточно. Приходится прибегать к использованию ряда дополнительных методов. Первый из них заключается в интегрировании функции путем ее подведения под знак дифференциала: ∫f(d(x)z'(x)dx=∫f(u)d(u)
Под u подразумевается сложная функция, которая и преобразовывается в простую.

4 Существует также несколько более сложный метод, который обычно применяется в случае, если необходимо проинтегрировать сложную тригонометрическую функцию. Он заключается в интегрировании по частям. Выглядит это следующим образом: ∫udv=uv-∫vdu Представьте себе, например, что дан интеграл ∫x*sinx dx. Обозначьте х как u, а dv - как sinxdx. Соответственно, v=-cosx, а du=1 Подставляя эти значения в вышеуказанную формулу, получите следующее выражение:
∫x*sinxdx=-x *cosx-∫(-cosx)=sinx-x*cosx+C, где С=const.

5 Еще один метод заключается в замене переменной. Он применяется в том случае, если под знаком интеграла имеются выражения со степенями или корнями. Формула замены переменной обычно имеет следующий вид:
[∫f(x)dx]=∫f[z(t)]z'(t)dt, причем, t=z(t)

Задания 5. Вычислить интеграл.

В общем виде определенный интеграл записывается так:

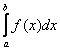
Прибавились пределы интегрирования.

Нижний предел интегрирования стандартно обозначается буквой .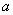
Верхний предел интегрирования стандартно обозначается буквой .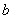
Отрезок 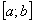называется отрезком интегрирования. У определенного интеграла есть геометрический смысл. Самая популярная задача – вычисление площади с помощью определенного интеграла. Решить определенный интеграл – это значит, найти число. Решить определенный интеграл можно с помощью формулы Ньютона-Лейбница:

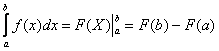
ВАРИАНТЫ ЗАДАНИЙ

Вариант - 1

1. Найти предел:

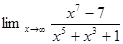
2. Найти производную:

а) 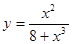б)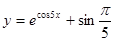

3. Исследовать функцию и построить график:

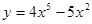
4. Найти неопределенный интеграл:

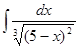
5. Вычислить интеграл:

Вариант - 2

1. Найти предел:

2. Найти производную:

а) 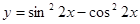б)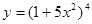

3. Исследовать функцию и построить график:

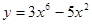
4. Найти неопределенный интеграл:

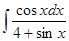
5. Вычислить интеграл:

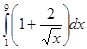
Вариант - 3

1. Найти предел:

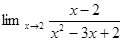
2. Найти производную:

а) 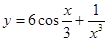б)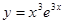

3. Исследовать функцию и построить график:

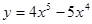
4. Найти неопределенный интеграл:

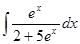
5. Вычислить интеграл:

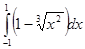
Вариант - 4

1. Найти предел:

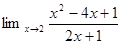
2. Найти производную:

а) 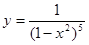б)

3. Исследовать функцию и построить график:

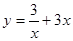
4. Найти неопределенный интеграл:

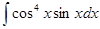
5. Вычислить интеграл:

Вариант - 5

1. Найти предел:

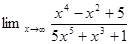
2. Найти производную:

а) 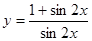б)

3. Исследовать функцию и построить график:

4. Найти неопределенный интеграл:

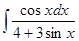
5. Вычислить интеграл:

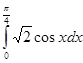
Вариант - 6

1. Найти предел:

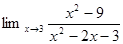
2. Найти производную:

а) 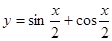б)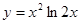

3. Исследовать функцию и построить график:

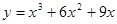
4. Найти неопределенный интеграл:

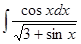
5. Вычислить интеграл:

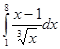
Вариант - 7

1. Найти предел:

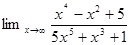
2. Найти производную:

а) 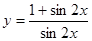б)

3. Исследовать функцию и построить график:

4. Найти неопределенный интеграл:

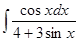
5. Вычислить интеграл:

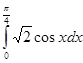
Вариант - 8

1. Найти предел:

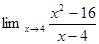
2. Найти производную:

а) 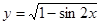б)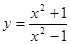

3. Исследовать функцию и построить график:

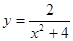
4. Найти неопределенный интеграл:

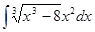
5. Вычислить интеграл:

Вариант - 9

1. Найти предел:

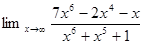
2. Найти производную:

а) б)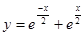

3. Исследовать функцию и построить график:

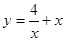
4. Найти неопределенный интеграл:

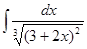
5. Вычислить интеграл:

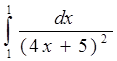
Вариант - 10

1. Найти предел:

2. Найти производную:

а) 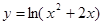б)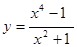

3. Исследовать функцию и построить график:

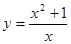
4. Найти неопределенный интеграл:

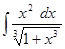
5. Вычислить интеграл:

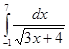
Вариант – 11

1. Найти предел:

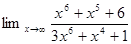
2. Найти производную:

а) 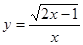б)

3. Исследовать функцию и построить график:

4. Найти неопределенный интеграл:

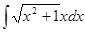
5. Вычислить интеграл:

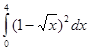
Вариант – 12

1. Найти предел:

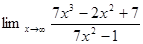
2. Найти производную:

а) 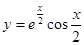б)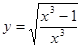

3. Исследовать функцию и построить график:

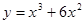
4. Найти неопределенный интеграл:

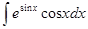
5. Вычислить интеграл:

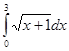
Вариант - 13

1. Найти предел:

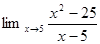
2. Найти производную:

а) 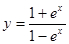б)

3. Исследовать функцию и построить график:

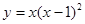
4. Найти неопределенный интеграл:

5. Вычислить интеграл:

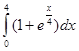
Вариант - 14

1. Найти предел:

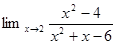
2. Найти производную:

а) 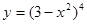б)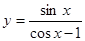

3. Исследовать функцию и построить график:

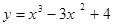
4. Найти неопределенный интеграл:

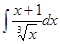
5. Вычислить интеграл:

Вариант - 15

1. Найти предел:

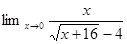
2. Найти производную:

а) 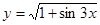б)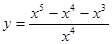

3. Исследовать функцию и построить график:

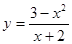
4. Найти неопределенный интеграл:

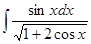
5. Вычислить интеграл:

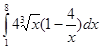
Вариант – 16

1. Найти предел:

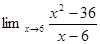
2. Найти производную:

а) 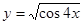б)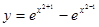

3. Исследовать функцию и построить график:

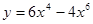
4. Найти неопределенный интеграл:

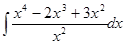
5. Вычислить интеграл:

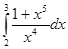
Вариант – 17

1. Найти предел:

2. Найти производную:

а) б)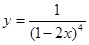

3. Исследовать функцию и построить график:

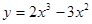
4. Найти неопределенный интеграл:

5. Вычислить интеграл:

Вариант – 18

1. Найти предел:

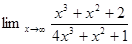
2. Найти производную:

а) 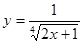б)

3. Исследовать функцию и построить график:

4. Найти неопределенный интеграл:

5. Вычислить интеграл:

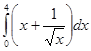
Вариант – 19

1. Найти предел:

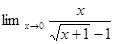
2. Найти производную:

а) 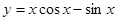б)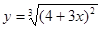

3. Исследовать функцию и построить график:

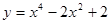
4. Найти неопределенный интеграл:

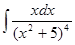
5. Вычислить интеграл:

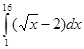
Вариант – 20

1. Найти предел:

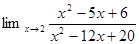
2. Найти производную:

а) 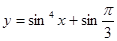б)

3. Исследовать функцию и построить график:

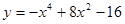
4. Найти неопределенный интеграл:

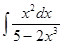
5. Вычислить интеграл:

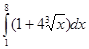
Вариант – 21

1. Найти предел:

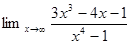
2. Найти производную:

а) 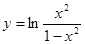б)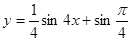

3. Исследовать функцию и построить график:

4. Найти неопределенный интеграл:

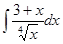
5. Вычислить интеграл:

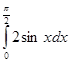
Вариант – 22

1. Найти предел:

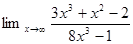
2. Найти производную:

а) 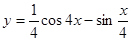б)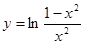

3. Исследовать функцию и построить график:

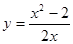
4. Найти неопределенный интеграл:

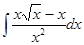
5. Вычислить интеграл:

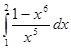
Вариант – 23

1. Найти предел:

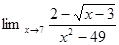
2. Найти производную:

а) 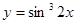б)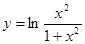

3. Исследовать функцию и построить график:

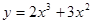
4. Найти неопределенный интеграл:

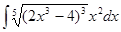
5. Вычислить интеграл:

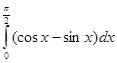
Вариант – 24

1. Найти предел:

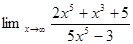
2. Найти производную:

а) б)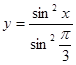

3. Исследовать функцию и построить график:

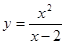
4. Найти неопределенный интеграл:

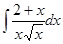
5. Вычислить интеграл:

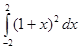
Вариант – 25

1. Найти предел:

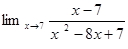
2. Найти производную:

а) б)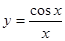

3. Исследовать функцию и построить график:

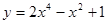
4. Найти неопределенный интеграл:

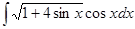
5. Вычислить интеграл:

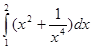
ВАРИАНТ – 26

1. Найти предел:

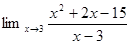
2. Найти производную:

а) 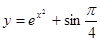б)

3. Исследовать функцию и построить график:

4. Найти неопределенный интеграл:

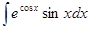
5. Вычислить интеграл:

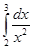
ВАРИАНТ – 27

1. Найти предел:

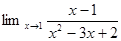
2. Найти производную:

а) 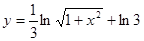б)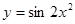

3. Исследовать функцию и построить график:

4. Найти неопределенный интеграл:

5. Вычислить интеграл:

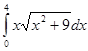
ВАРИАНТ – 28

1. Найти предел:

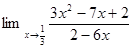
2. Найти производную:

а) 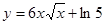б)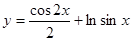

3. Исследовать функцию и построить график:

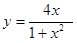
4. Найти неопределенный интеграл:

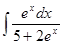
5. Вычислить интеграл:

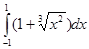
ВАРИАНТ – 29

1. Найти предел:

2. Найти производную:

а) 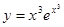б)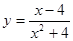

3. Исследовать функцию и построить график:

4. Найти неопределенный интеграл:

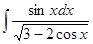
5. Вычислить интеграл:

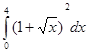
ВАРИАНТ – 30

1. Найти предел:

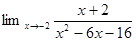
2. Найти производную:

а) 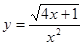б)

3. Исследовать функцию и построить график:

4. Найти неопределенный интеграл:

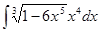
5. Вычислить интеграл:

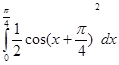
ВАРИАНТ – 31

1. Найти предел:

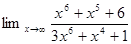
2. Найти производную:

а) 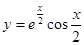б)

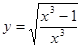
3. Исследовать функцию и построить график:

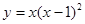
4. Найти неопределенный интеграл:

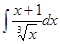
5.Вычислить интеграл:

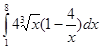
ВАРИАНТ – 32

1. Найти предел:

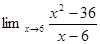
2. Найти производную:

а) 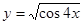б)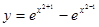

3. Исследовать функцию и построить график:

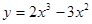
4. Найти неопределенный интеграл:

5. Вычислить интеграл:

ВАРИАНТ – 33

1. Найти предел:

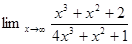
2. Найти производную:

а) 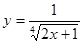б)

3. Исследовать функцию и построить график:

4. Найти неопределенный интеграл:

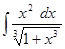
5. Вычислить интеграл:

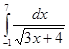
ВАРИАНТ – 34

1. Найти предел:

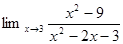
2. Найти производную:

а) 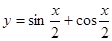б)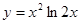

3. Исследовать функцию и построить график:

4. Найти неопределенный интеграл:

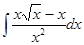
5. Вычислить интеграл:

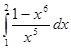
ВАРИАНТ – 35

1. Найти предел:

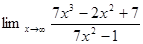
2. Найти производную:

а) 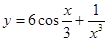б)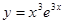

3. Исследовать функцию и построить график:

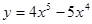
4. Найти неопределенный интеграл:

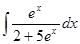
5. Вычислить интеграл:

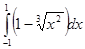
ВАРИАНТ – 36

1. Найти предел:

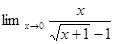
2. Найти производную:

а) 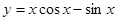б)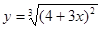

3. Исследовать функцию и построить график:

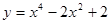
4. Найти неопределенный интеграл:

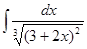
5. Вычислить интеграл:

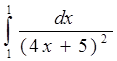
ВАРИАНТ – 37

1. Найти предел:

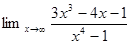
2. Найти производную:

а) 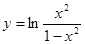б)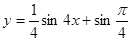

3. Исследовать функцию и построить график:

4. Найти неопределенный интеграл:

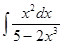
5. Вычислить интеграл:

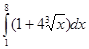
ВАРИАНТ – 38

1. Найти предел:

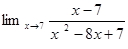
2. Найти производную:

а) б)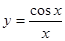

3. Исследовать функцию и построить график:

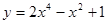
4. Найти неопределенный интеграл:

5. Вычислить интеграл:

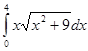
ВАРИАНТ – 39

1. Найти предел:

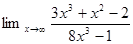
2. Найти производную:

а) 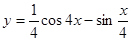б)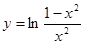

3. Исследовать функцию и построить график:

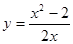
4. Найти неопределенный интеграл:

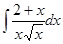
5. Вычислить интеграл:

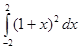
ВАРИАНТ – 40

1. Найти предел:

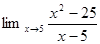
2. Найти производную:

а) 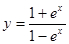б)

3. Исследовать функцию и построить график:

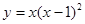
4. Найти неопределенный интеграл:

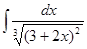
5. Вычислить интеграл:

Дата добавления: 2017-01-13