Понятие об интегрирующем множителе

КОНОНОВА О.А., ИЛЬИНКОВА Н.И., РОМАНОВА Н.С.

ИНТЕГРИРУЮЩИЙ МНОЖИТЕЛЬ

УРАВНЕНИЯ В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ

ДИФФЕРЕНЦИАЛЬНЫЕ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ

Учебно-методическое пособие для студентов

физического факультета специальности

1-31 04 01 «Физика»,

радиофизического факультета специальностям

1-31 04 02 «Радиофизика»,

1-31 04 03 «Физическая электроника»,

1-98 01 01-02 «Компьютерная безопасность»

Минск 2009 г.

Учебно-методическое пособие по курсу «Дифференциальные и интегральные уравнения. Уравнения в полных дифференциалах. Интегрирующий множитель» предназначено для самостоятельного изучения и последующего контроля полученных знаний по теме «Уравнения в полных дифференциалах. Интегрирующий множитель» студентов I курса физического и II курса радиофизического факультетов Белорусского государственного университета.

Ответственный за выпуск: Н.С.Романова.

В односвязной области рассмотрим уравнение вида

, (1)

где M (x, y), N (x, y), непрерывно дифференцируемые функции. Уравнение (1) называется уравнением в полных дифференциалах, если выполнено условие

. (2)

Тогда существует такая функция u (x, y), что левая часть уравнения (1) является ее полным дифференциалом

. (3)

Уравнение в полных дифференциалах всегда интегрируется в квадратурах.

Если условие (2) не выполняется, то уравнение (1) не является уравнением в полных дифференциалах. Возникает вопрос: «Если уравнение (1) не является «в полных дифференциалах», то можно ли его привести к уравнению в полных дифференциалах?» Во многих случаях удается найти функцию , после умножения, на которую уравнение не в полных дифференциалах (1) преобразуется в уравнение в полных дифференциалах

, (4)

т.е. .

Функция в уравнении (4) называется интегрирующим множителем, а U (x, y) ‑ соответствующим ему интегралом уравнения (1), U (x, y)= С.

2. Нахождение интегрирующего множителя

Интегрирующий множитель имеет непрерывные частные производные первого порядка. Поэтому учитывая, что

,

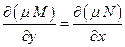получим уравнение с частными производными первого порядка с неизвестной функцией

. (5)

В некоторых случаях удается найти решение уравнения (4) и тем самым найти интегрирующий множитель уравнения (1).

I. Случай интегрирующего множителя вида .

Для интегрирующего множителя этого типа уравнение (5) имеет следующий вид:

, (6)

отсюда получим .

Если обозначить , то . Здесь при , содержится случай интегрирующего множителя, зависящего только от x или только y.

II. Интегрирующий множитель , зависящий только от произведения xy, существует, если

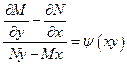, где .

III. Интегрирующий множитель , зависящий только от суммы x + y, существует, если

, где .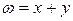

Рассмотрим следующие примеры решения дифференциальных уравнений с помощью нахождения интегрирующего множителя.

Дата добавления: 2017-01-13