
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уравнения, не разрешенные относительно производной
|
|
|
|
Линейные уравнения
40. Найти кривые, у которых площадь трапеции, ограниченной осями координат, касательной и ординатой точки касания, есть величина постоянная, равная 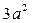 .
.
41. Найти кривые, у которых площадь треугольника, ограниченного касательной, осью абсцисс и отрезком от начала координат до точки касания, есть величина постоянная, равная  .
.
42. В баке находится 100  раствора, содержащего 10
раствора, содержащего 10  соли. В бак втекает 5
соли. В бак втекает 5  воды в минуту, а смесь с той же скоростью переливается в другой 100-литровый бак, первоначально наполненный чистой водой. Избыток жидкости из него выливается. Когда количество соли во втором баке будет наибольшим? Чему оно равно?
воды в минуту, а смесь с той же скоростью переливается в другой 100-литровый бак, первоначально наполненный чистой водой. Избыток жидкости из него выливается. Когда количество соли во втором баке будет наибольшим? Чему оно равно?
43. За время  (где
(где  очень мало и выражено в долях года) из каждого грамма радия распадается
очень мало и выражено в долях года) из каждого грамма радия распадается  грамма и образуется
грамма и образуется  грамма радона. Из каждого грамма радона за время
грамма радона. Из каждого грамма радона за время  распадается
распадается  грамма. В начале опыта имелось некоторое количество
грамма. В начале опыта имелось некоторое количество  чистого радия. Когда количество образовавшегося и еще не распавшегося радона будет наибольшим?
чистого радия. Когда количество образовавшегося и еще не распавшегося радона будет наибольшим?
44. Найти кривую, каждая касательная к которой образует с осями координат треугольник с постоянной площадью 2  .
.
45. Найти кривую, для которой отрезок касательной, заключенный между координатными осями, имеет постоянную длину  .
.
46. Найти кривую, каждая касательная к которой отсекает на осях координат такие отрезки, что сумма величин, обратных квадратам длин этих отрезков, равна 1.
47. Найти кривую, проходящую через начало координат и такую, что отрезок нормали к ней, отсекаемый сторонами первого координатного угла, имеет постоянную длину, равную 2.
К разделу 2. Уравнения, допускающие понижение порядка
48. Определить кривую, у которой радиус кривизны равен постоянной величине.
49. Найти кривые, у которых в любой точке радиус кривизны вдвое больше отрезка нормали, заключенного между этой точкой кривой и осью абсцисс. Рассмотреть два случая: а) кривая обращена выпуклостью к оси абсцисс; б) вогнутостью к оси абсцисс.
50. Найти кривые, у которых радиус кривизны обратно пропорционален косинусу угла между касательной и осью абсцисс.
51. Найти кривую, проходящую через начало координат и такую, что площадь треугольника, образованного касательной к кривой в некоторой точке, ординатой этой точки и осью абсцисс, прямо пропорциональна площади криволинейной трапеции, образованной кривой, осью абсцисс и ординатой этой точки.
52. Определить форму равновесия нерастяжимой нити с закрепленными концами, на которую действует нагрузка так, что на каждую единицу длины горизонтальной проекции нагрузка одинакова (цепи цепного моста). Весом самой нити пренебречь.
53. Найти форму равновесия однородной нерастяжимой нити с закрепленными концами под действием ее веса.
54. Найти время, нужное телу для того, чтобы упасть на Землю в высоты 400000  (приблизительное расстояние от Луны к центру Земли), если радиус Земли равен приблизительно 6400
(приблизительное расстояние от Луны к центру Земли), если радиус Земли равен приблизительно 6400  .
.
55. Найти скорость, с которой тело упадет на поверхность Земли, если считать, что оно падает с бесконечно большой высоты и движение происходит только под влиянием притяжения Земли. Радиус Земли считать равным 6400  .
.
56. Найти закон движения материальной точки массы  по прямой
по прямой  под действием отталкивающей силы, обратно пропорциональной третьей степени расстояния точки
под действием отталкивающей силы, обратно пропорциональной третьей степени расстояния точки  от неподвижного центра
от неподвижного центра 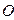 .
.
57. Тело массой  падает с некоторой высоты. При падении тело испытывает сопротивление, прямо пропорциональное квадрату скорости. Найти закон движения падающего тела.
падает с некоторой высоты. При падении тело испытывает сопротивление, прямо пропорциональное квадрату скорости. Найти закон движения падающего тела.
58. Найти закон движения тела, падающего без начальной скорости, допуская, что сопротивление воздуха прямо пропорционально квадрату скорости и что скорость имеет своим пределом при  величину
величину
75  .
.
К разделу 3. Линейные уравнения
59. Найти уравнение движения точки, если ускорение в зависимости от времени выражается формулой 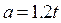 , и если при
, и если при  расстояние
расстояние 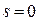 , а при
, а при  расстояние
расстояние 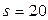 .
.
60. Цепь длиной 6 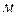 соскальзывает со стола. В момент начала движения со стола свисал 1
соскальзывает со стола. В момент начала движения со стола свисал 1 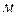 цепи. За какое время со стола соскользнет вся цепь? Трением пренебречь.
цепи. За какое время со стола соскользнет вся цепь? Трением пренебречь.
61. Цепь переброшена через гладкий гвоздь. В момент начала движения с одной стороны свисает 8  цепи, а с другой стороны – 10
цепи, а с другой стороны – 10  цепи. За какое время вся цепь соскользнет с гвоздя? Трением пренебречь.
цепи. За какое время вся цепь соскользнет с гвоздя? Трением пренебречь.
62. Тело массой  скользит по горизонтальной плоскости под действием толчка, давшего начальную скорость
скользит по горизонтальной плоскости под действием толчка, давшего начальную скорость  . На тело действует сила трения, равная
. На тело действует сила трения, равная  . Найти расстояние, которое тело способно пройти.
. Найти расстояние, которое тело способно пройти.
63. Поезд движется по горизонтальному пути. Вес поезда – 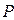 , сила тяги паровоза
, сила тяги паровоза  , сила сопротивления при движении –
, сила сопротивления при движении –  , где
, где  и
и  – постоянные,
– постоянные,  – скорость поезда;
– скорость поезда;  – пройденный путь. Определить закон движения поезда, считая, что при
– пройденный путь. Определить закон движения поезда, считая, что при 
 и
и  .
.
64. Материальная точка массой  отталкивается от центра
отталкивается от центра 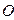 с силой, прямо пропорциональной расстоянию. Сопротивление среды прямо пропорционально скорости движения. Найти закон движения.
с силой, прямо пропорциональной расстоянию. Сопротивление среды прямо пропорционально скорости движения. Найти закон движения.
65. Материальная точка массы  движется прямолинейно, приближаясь к центру, отталкивающему ее с силой, равной
движется прямолинейно, приближаясь к центру, отталкивающему ее с силой, равной  , где
, где  – расстояние от точки до центра. Найти закон движения, если в начальный момент времени точка находилась от центра на расстоянии
– расстояние от точки до центра. Найти закон движения, если в начальный момент времени точка находилась от центра на расстоянии  и имела скорость
и имела скорость 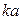 .
.
66. Материальная точка медленно погружается в жидкость. Найти закон движения, считая, что при медленном погружении сопротивление жидкости прямо пропорционально скорости погружения.
В задачах 67–71 принять, что при отклонении груза от положения равновесия на расстояние  пружина действует на него с силой
пружина действует на него с силой 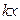 , направленной к положению равновесия.
, направленной к положению равновесия.
67. Найти период свободных колебаний массы  , подвешенной к пружине, если движение происходит без сопротивления.
, подвешенной к пружине, если движение происходит без сопротивления.
68. Груз массой 
 подвешен на пружине и оттянул ее на
подвешен на пружине и оттянул ее на 
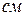 . Затем пружина оттягивается еще на
. Затем пружина оттягивается еще на 
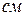 и отпускается без начальной скорости. Найти закон движения пружины, пренебрегая сопротивлением среды.
и отпускается без начальной скорости. Найти закон движения пружины, пренебрегая сопротивлением среды.
69. Два одинаковых груза подвешены к концу пружины. Найти закон движения одного из грузов, если другой оборвется. Дано, что удлинение пружины под влиянием одного из грузов равно 
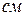 .
.
70. Один конец пружины закреплен неподвижно, а к другому прикреплен груз массой  При движении груза со скоростью
При движении груза со скоростью  сила сопротивления равна
сила сопротивления равна 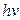 . При
. При  грузу, находившемуся в положении равновесия, сообщена скорость
грузу, находившемуся в положении равновесия, сообщена скорость 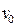 . Исследовать движение груза в случаях
. Исследовать движение груза в случаях  и
и  .
.
71. Решить предыдущую задачу при дополнительном условии, что к грузу приложена еще периодическая внешняя сила  . Показать, что при любых начальных условиях движение груза будет приближаться к периодическому и найти это периодическое движение (вынужденные колебания).
. Показать, что при любых начальных условиях движение груза будет приближаться к периодическому и найти это периодическое движение (вынужденные колебания).
72. Частица массой  движется по оси
движется по оси  , отталкиваясь от точки
, отталкиваясь от точки 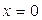 с силой
с силой 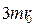 и притягиваясь к точке
и притягиваясь к точке  с силой
с силой  , где
, где  и
и  – расстояния до этих точек. Определить движение частицы с начальными условиями
– расстояния до этих точек. Определить движение частицы с начальными условиями 
В задачах 73 – 78 можно пользоваться следующими законами теории электрических цепей:
1) для каждого узла цепи сумма всех притекающих токов равна сумме вытекающих токов;
2) алгебраическая сумма напряжений источников тока, содержащихся в любом замкнутом контуре цепи, равна алгебраической сумме падений напряжений на всех остальных участках этого контура.
Имеем:
падение напряжения на сопротивлении  равно
равно 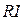 ;
;
падение напряжения на самоиндукции  равно
равно 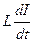 ;
;
падение напряжения на конденсаторе емкости  равно
равно 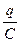 , где
, где  – заряд конденсатора в момент времени
– заряд конденсатора в момент времени 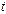 ; при этом
; при этом  ;
;
во всех трех случаях  – сила тока, протекающего через рассматриваемый участок цепи в данный момент
– сила тока, протекающего через рассматриваемый участок цепи в данный момент 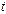 .
.
В этих формулах  выражается в амперах,
выражается в амперах,  – в омах,
– в омах,  – в генри,
– в генри, 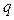 – в кулонах,
– в кулонах,  – в фарадах,
– в фарадах, 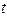 – в секундах, напряжение – в вольтах.
– в секундах, напряжение – в вольтах.
73. Электрическая цепь состоит из последовательно включенных источника постоянного тока, дающего напряжение  , сопротивления
, сопротивления  , самоиндукции
, самоиндукции  и выключателя, который включается при
и выключателя, который включается при  . Найти зависимость силы тока от времени.
. Найти зависимость силы тока от времени.
74. Решить предыдущую задачу, заменив самоиндукцию  конденсатором емкости
конденсатором емкости  . Конденсатор до замыкания цепи не заряжен.
. Конденсатор до замыкания цепи не заряжен.
75. Последовательно включены сопротивление  и конденсатор емкости
и конденсатор емкости  , заряд которого при
, заряд которого при  равен
равен 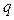 . Цепь замыкается при
. Цепь замыкается при  . Найти силу тока в цепи в зависимости от времени.
. Найти силу тока в цепи в зависимости от времени.
76. Последовательно включены самоиндукция  , сопротивление
, сопротивление  и конденсатор емкости
и конденсатор емкости  , заряд которого при
, заряд которого при  равен
равен 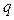 . Цепь замыкается при
. Цепь замыкается при  . Найти силу тока в цепи и частоту колебаний в том случае, когда разряд носит колебательный характер.
. Найти силу тока в цепи и частоту колебаний в том случае, когда разряд носит колебательный характер.
77. Последовательно включены источник тока, напряжение которого меняется по закону  , сопротивление
, сопротивление  и самоиндукция
и самоиндукция  . Найти силу тока в цепи (установившийся режим).
. Найти силу тока в цепи (установившийся режим).
78. Последовательно включены источник тока, напряжение которого меняется по закону  , сопротивление
, сопротивление  , самоиндукция
, самоиндукция  и емкость
и емкость  . Найти силу тока в цепи (установившийся режим). При какой частоте
. Найти силу тока в цепи (установившийся режим). При какой частоте  сила тока наибольшая?
сила тока наибольшая?
К разделу 4. Линейные системы
79. Тело массой  движется на плоскости
движется на плоскости  , притягиваясь к точке
, притягиваясь к точке 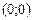 с силой
с силой 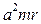 , где
, где 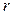 – расстояние до этой точки. Найти движение тела при начальных условиях:
– расстояние до этой точки. Найти движение тела при начальных условиях:  и траекторию этого движения.
и траекторию этого движения.
80. Один конец пружины закреплен неподвижно в точке 0, а к другому прикреплен груз массой  , соединенный другой пружиной с грузом массы
, соединенный другой пружиной с грузом массы  . Оба груза двигаются без трения по одной прямой, проходящей через точку 0. Каждая из пружин растягивается на величину
. Оба груза двигаются без трения по одной прямой, проходящей через точку 0. Каждая из пружин растягивается на величину  под действием силы
под действием силы  . Найти возможные периодические движения системы.
. Найти возможные периодические движения системы.
81. На концах вала закреплены два шкива, моменты инерции которых  и
и 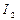 . При повороте одного шкива относительно другого на любой угол
. При повороте одного шкива относительно другого на любой угол 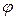 вследствие деформации вала возникают упругие силы с крутящим моментом
вследствие деформации вала возникают упругие силы с крутящим моментом  . Найти частоту крутильных колебаний вала при отсутствии внешних сил.
. Найти частоту крутильных колебаний вала при отсутствии внешних сил.
К разделу 5. Уравнения в частных производных первого порядка
82. Найти общее уравнение поверхностей, пересекающих под прямым углом поверхности семейства 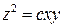 .
.
83. Найти поверхность, проходящую через прямую 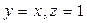 , и ортогональную к поверхностям
, и ортогональную к поверхностям  .
.
84. Написать уравнение в частных производных, которому удовлетворяют цилиндрические поверхности с образующими, параллельными вектору 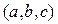 . Найти общее решение этого уравнения.
. Найти общее решение этого уравнения.
85. Пользуясь результатом предыдущей задачи, найти уравнение цилиндрической поверхности с образующими, параллельными вектору  , и направляющей
, и направляющей  .
.
86. Написать уравнение в частных производных, которому удовлетворяют все конические поверхности с вершиной в данной точке 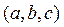 , и решить его.
, и решить его.
87. Найти поверхности, у которых любая касательная плоскость пересекает ось 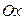 в точке с абсциссой, вдвое меньшей абсциссы точки касания.
в точке с абсциссой, вдвое меньшей абсциссы точки касания.
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 1199; Нарушение авторских прав?; Мы поможем в написании вашей работы!