
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Число Рейнольдса характеризует соотношение между силами инерции и молекулярного трения (вязкости), которое определяет гидродинамический режим вынужденного движения среды
|
|
|
|
Пограничным слоем называют область течения (вблизи стенки) вязкой теплопроводной жидкости, характеризуемую малой толщиной и большим поперечным градиентом скорости или температуры, изменением которых обусловлены процессы переноса вещества, количества движения и теплоты.
Под внешним потоком подразумевают область потока жидкости, в которой влияние сил вязкости ничтожно мало по сравнению с силами инерции, в то время как в пограничном слое силы вязкости и инерции соизмеримы.
Толщина пограничного слоя  — величина условная, так как переход от пограничного слоя к внешнему потоку не является резким. За толщину пограничного слоя
— величина условная, так как переход от пограничного слоя к внешнему потоку не является резким. За толщину пограничного слоя  принимают расстояние от поверхности стенки до слоя жидкости, скорость которого отличается от скорости внешнего потока на малую, заранее заданную величину.
принимают расстояние от поверхности стенки до слоя жидкости, скорость которого отличается от скорости внешнего потока на малую, заранее заданную величину.
При теплообмене между стенкой и средой в области, граничащей с поверхностью тела, возникает тепловой пограничный слой, представляющий собой пристенный слой жидкости, в котором температура меняется от температуры стенки  до температуры внешнего потока
до температуры внешнего потока 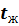 .
.
Термическое сопротивление пограничного слоя  во много раз превышает термическое сопротивление турбулентного внешнего потока и является определяющим в процессах конвективного теплообмена. Поэтому изменение температуры от
во много раз превышает термическое сопротивление турбулентного внешнего потока и является определяющим в процессах конвективного теплообмена. Поэтому изменение температуры от 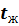 до
до  сосредоточено в основном в пределах пограничного слоя.
сосредоточено в основном в пределах пограничного слоя.
| 1.2 | УРАВНЕНИЕ КОНВЕКТИВНОГО ТЕПЛООБМЕНА |
И. Ньютон впервые обратил внимание на то, что разность температур является решающим фактором в процессе теплообмена между телом и средой. В ХVIII в. русский физик Г. Рихман первым дал обстоятельный анализ процессов охлаждения нагретых тел в воздухе и показал их зависимость не только от разности температур, но и от площади поверхности и объема тела.
Последующие исследования выявили большую сложность процессов теплообмена, тесно переплетающихся с гидродинамическими процессами. Было найдено, что в процессе теплообмена количество теплоты, отдаваемой или получаемой телом от окружающей среды, прямо пропорционально площади поверхности тела  , разности температур поверхности тела
, разности температур поверхности тела  и среды (жидкости)
и среды (жидкости) 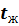 , длительности процесса, а также зависит от физических свойств среды, характера ее движения, формы тела и его геометрических размеров. Для элементарной площадки и элементарного времени процесс описывается уравнением
, длительности процесса, а также зависит от физических свойств среды, характера ее движения, формы тела и его геометрических размеров. Для элементарной площадки и элементарного времени процесс описывается уравнением

| (1) |
названным основным уравнением конвективного теплообмена или законом Ньютона–Рихмана.
В уравнении (1)  – температурный напор;
– температурный напор;  – коэффициент пропорциональности, названный коэффициентом теплоотдачи, Вт/(м2 × К).
– коэффициент пропорциональности, названный коэффициентом теплоотдачи, Вт/(м2 × К).
Для стационарного процесса теплообмена при неизменных температуре среды и площади поверхности тепловой поток

| (2) |
а плотность теплового потока

| (3) |
Из уравнения Ньютона–Рихмана имеем

| (4) |
т. е. коэффициент теплоотдачи равен количеству теплоты, воспринимаемой (или отдаваемой) единицей поверхности в единицу времени при разности температур между поверхностью и движущейся средой в 1 К.
Коэффициент теплоотдачи характеризует интенсивность теплообмена между поверхностью тела и омывающей средой и учитывает конкретные условия протекания этого процесса. Так как  зависит от скорости движения среды
зависит от скорости движения среды  , формы поверхности тела
, формы поверхности тела  , его линейных размеров
, его линейных размеров  ,
, 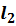 ,..., ориентации поверхности в пространстве, температурного напора
,..., ориентации поверхности в пространстве, температурного напора  , температуры среды
, температуры среды 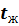 и т. п., то коэффициент теплоотдачи, в отличие от коэффициентов теплопроводности и температуропроводности, не является теплофизической характеристикой вещества, и его значения не приводятся в справочниках.
и т. п., то коэффициент теплоотдачи, в отличие от коэффициентов теплопроводности и температуропроводности, не является теплофизической характеристикой вещества, и его значения не приводятся в справочниках.
Наиболее существенное влияние на величину  оказывают коэффициент теплопроводности
оказывают коэффициент теплопроводности  , удельная теплоемкость
, удельная теплоемкость  , плотность
, плотность  , динамическая вязкость
, динамическая вязкость  (или кинематическая вязкость
(или кинематическая вязкость  ), коэффициент объемного расширения
), коэффициент объемного расширения  .
.
Все реальные жидкости обладают вязкостью. Вязкость — свойство жидкости оказывать сопротивление перемещению (сдвигу) ее слоев. Динамическая вязкость  характеризует собой силу, которая возникает на квадратном метре поверхности двух перемещающихся друг относительно друга слоев жидкости при градиенте скорости
характеризует собой силу, которая возникает на квадратном метре поверхности двух перемещающихся друг относительно друга слоев жидкости при градиенте скорости  . В уравнениях теплопередачи и гидродинамики часто используют кинематическую вязкость
. В уравнениях теплопередачи и гидродинамики часто используют кинематическую вязкость  .
.
При кажущейся простоте расчета процесса теплоотдачи по формуле (2) оказывается, что определить коэффициент теплоотдачи  задача довольно трудная. Аналитическое определение
задача довольно трудная. Аналитическое определение  наталкивается на математические трудности, которые не обеспечивают нужную точность вычисления, а в большинстве случаев оказываются непреодолимыми. В настоящее время теоретически решено всего несколько задач конвективного теплообмена. Поэтому коэффициент
наталкивается на математические трудности, которые не обеспечивают нужную точность вычисления, а в большинстве случаев оказываются непреодолимыми. В настоящее время теоретически решено всего несколько задач конвективного теплообмена. Поэтому коэффициент  в большинстве случаев определяют экспериментально. Но эксперимент не всегда осуществим на практике, а результаты отдельных опытов справедливы только для данного конкретного случая. На помощь приходит теория подобия, позволяющая распространить результаты единичного опыта на группу подобных явлений.
в большинстве случаев определяют экспериментально. Но эксперимент не всегда осуществим на практике, а результаты отдельных опытов справедливы только для данного конкретного случая. На помощь приходит теория подобия, позволяющая распространить результаты единичного опыта на группу подобных явлений.
| 1.3 | ОСНОВЫ ТЕОРИИ ПОДОБИЯ |

| Рис. 2. Геометрическое подобие плоских фигур |
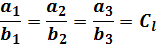
| или | 
|
Величина  – константа геометрического подобия. По аналогии можно утверждать, что прямые трубы подобны, если соблюдается равенство
– константа геометрического подобия. По аналогии можно утверждать, что прямые трубы подобны, если соблюдается равенство

|
где  ,
,  ,
,  – диаметры труб, а
– диаметры труб, а  ,
, 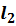 ,
,  – их длина. Понятие подобия может быть распространено и на любые физические величины, а также процессы и явления.
– их длина. Понятие подобия может быть распространено и на любые физические величины, а также процессы и явления.
Для сложных процессов, характеризующихся многими физическими величинами, каждая переменная величина имеет свою константу подобия  . Если явления подобны, то константы подобия находятся между собой в определенных соотношениях и для данного процесса (системы) их выбор обусловлен условием подобия физических явлений. Эти безразмерные соотношения представляют собой комплексы, составленные из физических величин, характеризующих это явление (процесс). Называются они критериями (числами) подобия. Для всех подобных явлений критерии подобия имеют одинаковое числовое значение.
. Если явления подобны, то константы подобия находятся между собой в определенных соотношениях и для данного процесса (системы) их выбор обусловлен условием подобия физических явлений. Эти безразмерные соотношения представляют собой комплексы, составленные из физических величин, характеризующих это явление (процесс). Называются они критериями (числами) подобия. Для всех подобных явлений критерии подобия имеют одинаковое числовое значение.
Таким образом, критерием подобия называется безразмерный комплекс, составленный из величин, существенных для данного процесса.
Все критерии подобия имеют определенный физический смысл, а их нулевая размерность может служить проверкой правильности их составления. Обычно их называют именами ученых, внесших большой вклад в изучение процессов теплообмена и гидродинамики, и обозначают начальными латинскими буквами фамилий.
Основная идея теории подобия заключается в том, что первое частное решение явления (искомую закономерность) получают экспериментально на модели, а результаты представляют в критериальном виде, что позволяет легко и быстро получать данные для других явлений, подобных модельному. Теория подобия дает общие методические указания по выбору величин, измеряемых в опыте, по обработке полученных результатов, по обобщению результатов эксперимента на другие явления, подобные исследованному, а также позволяет рассчитать и построить модель, подобную натуре.
Теория подобия базируется на трех теоремах. В знаменитой книге «Математические начала натуральной философии» И. Ньютон в 1686 г. на примере подобного течения двух жидкостей впервые распространил геометрическое подобие на физические явления. Но если Ньютон высказал только основную идею подобия физических явлений, то французский математик Ж. Бертран в 1848 г. дал строгое доказательство и установил основное свойство подобных явлений, названное позже первой теоремой подобия: подобные между собой явления имеют одинаковые критерии подобия. Эта теорема позволяет вывести уравнения для критериев подобия и указывает, что в опытах нужно измерять лишь те величины, которые содержатся в критериях подобия изучаемого процесса.
Следующий шаг в развитии теории подобия был сделан в начале нашего столетия, когда русский ученый А. Федерман в 1911 г. и американский физик Дж. Букингем в 1914 г. независимо друг от друга предложили вторую теорему подобия, согласно которой исходные математические уравнения, характеризующие данное физическое явление, всегда могут быть представлены в виде зависимости между критериями подобия, характеризующими это явление. Эти функциональные зависимости между критериями подобия называются уравнениями подобия или критериальными уравнениями. Из теоремы следует, что результаты опытов необходимо обрабатывать и представлять в виде критериальных уравнений.
Третья теорема подобия была предложена советскими учеными М. В. Кирпичевым и А. А. Гyxманом в 1936 г.: подобны те явления, условия однозначности которых подобны и для которых критерии подобия, составленные из условий однозначности, численно равны. Третья теорема устанавливает признаки, по которым определяют, какие явления подобны друг другу, т. е. она позволяет выявить те явления, на которые могут быть распространены результаты эксперимента, полученные на модели.
Все основные критерии подобия тепловых, механических и гидромеханических явлений получаются из математических уравнений, описывающих соответствующий процесс. Например, соотношение сил инерции
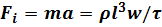
|
и массовых сил (сил тяжести)

|
в потоке жидкости характеризуется безразмерным комплексом:

|
который называется критерием Фруда:

| (5) |
где 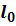 – определяющий линейный размер.
– определяющий линейный размер.
Критерий Фруда характеризует соотношение массовых сил (сил тяжести) и сил инерции при вынужденном движении жидкости. Число Фруда используется при испытании в опытных бассейнах моделей кораблей, глиссеров и т. п.
Связь между силами инерции  и давления
и давления  при вынужденном движении жидкости
при вынужденном движении жидкости

|
характеризуется критерием Эйлера

| (6) |
Из выражения (6) следует, что число Эйлера является мерой отношения перепада статических давлений в потоке (гидравлического сопротивления) к кинетической энергии потока.
Очень важным для решения задач гидродинамики и вынужденной конвекции является безразмерный комплекс, показывающий связь между силами инерции и силами вязкости
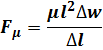
|

|
Комплекс назван критерием Рейнольдса:

| (7) |
Так как  , где
, где  – кинематическая вязкость, то
– кинематическая вязкость, то

| (8) |
При свободном движении среды (естественная конвекция), когда движение осуществляется только за счет разности плотностей, вызванной неравномерностью температурного поля, критерием подобия, определяющим распространение теплоты в среде, является критерий Грасгофа. Он находится из произведения числа Рейнольдса на отношение подъемной силы

|
к силе вязкости  :
:

|
Учитывая, что  , окончательно имеем
, окончательно имеем

| (9) |
где  – температурный коэффициент объемного расширения.
– температурный коэффициент объемного расширения.
Число Грасгофа характеризует соотношение между подъемной силой, возникающей в среде вследствие разности плотностей, и силой молекулярного трения (вязкости).
Таким образом, если речь идет о гидромеханическом подобии потоков, то для них в любых сходственных точках критерии подобия 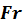 (или
(или 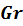 ),
),  и
и  имеют одинаковые значения.
имеют одинаковые значения.
Важнейшие критерии теплового подобия могут быть получены из основных уравнений передачи теплоты.
Количество теплоты, переда иной теплопроводностью, в соответствии с законом Фурье

| (10) |
Количество теплоты, переданной в процессе теплоотдачи, составляет

| (11) |
Теплота, воспринятая телом массой М,

| (12) |
Разделив (10) на (12), получаем безразмерный комплекс

|
являющийся одним из важнейших критериев подобия критерием Фурье:

| (13) |
где  – температуропроводность.
– температуропроводность.
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 2296; Нарушение авторских прав?; Мы поможем в написании вашей работы!