Теоретические сведения. Позиционные игры с полной информацией

Введение

Позиционные игры с полной информацией

Методические указания

по выполнению лабораторной работы

по курсу «Теория принятия решений

в условиях информационных конфликтов»

Калуга, 2014

УДК 681.3-7

ББК 32.973

Данные методические указания разработаны в соответствии с учебным планом специальности 090903.65 «Информационная безопасность автоматизированных систем».

Указания рассмотрены и одобрены:

кафедрой ЭИУ6-КФ «Информационная безопасность автоматизированных систем»

протокол № ___ от _____________ 2014 г.

Зав. кафедрой ЭИУ6-КФ ______________­­­­­__к.т.н., доц. Мазин А.В.

методической комиссией факультета ЭИУК

протокол № _____ от ____________________ 2014 г.

Председатель методической комиссии

факультета ЭИУК ___________________к.т.н., доц. Адкин М.Ю.

методической комиссией Калужского филиала МГТУ им. Н.Э. Баумана

протокол № _____ от ____________________ 2014 г.

Председатель методической комиссии

КФ МГТУ им. Н.Э. Баумана ___________________ к.т.н., доц. Малышев Е.Н.

Рецензент:

к.т.н., доц. кафедры ЭИУ3-КФ ___________________ Николаенко С.И.

Авторы ассистент кафедры ЭИУ6-КФ

____________Клочко Ольга Сергеевна

В методических указаниях изложены основные сведения о позиционных играх с полной информацией. Методическое пособие предназначено для студентов специальности 090303 «Информационная безопасность автоматизированных систем» и направления подготовки 230100 «Информатика и вычислительная техника» и может быть рекомендовано к применению при проведении лабораторных работ по дисциплине «Теория принятия решений в условиях информационного конфликта».

© Калужский филиал МГТУ им. Н.Э. Баумана, 2014 г.

© Кафедра ЭИУ6-КФ, 2014г.

© Клочко О.С., 2014г.

СОДЕРЖАНИЕ

Введение. 4

1. Теоретические сведения. 5

2. Практическая часть. 6

3. Задание. 6

4. Контрольные вопросы.. 7

Литература. 8

Тема работы: позиционные игры с полной информацией.

Требования к оборудованию:

• Компьютер уровня не ниже, чем Pentium/RAM 128 MB/HDD 1 GB;
• Операционная система Windows версии 2000 или выше с типовым вариантом установки;
• Среда разработки Microsoft Visual Studio версии 2005 или выше;
• Офисная программа Microsoft Office Word версии 2003 или выше с типовым вариантом установки.

Цель работы: получить практические навыки решения позиционных игр с полной информацией.

Содержание работы:

1. Изучение теоретических сведений о позиционных играх с полной информацией.

2. Получение практических навыков решения позиционных игр с полной информацией.

3. Оформление отчета.

Требования к отчету. Индивидуальный отчетстудента должен быть представлен в распечатанной форме с типовым титульным листом. Отчет должен содержать:

1. Задание.

2. Теоретические сведения.

3. Листинг программы.

4. Результат работы программы.

5. Вывод.

Длительность работы. 6 академических часов.

Защита работы: собеседование с преподавателем по контрольным вопросам.

Позиционная игра – это бескоалиционная игра, моделирующая процессы последовательного принятия решений игроками в условиях меняющейся во времени и, вообще говоря, неполной информации.

Процесс игры состоит в последовательном переходе от одного состояния игры к другому состоянию, который осуществляется либо путем выбора игроками одного из возможных действий в соответствии с правилами игры, либо случайным образом (случайный ход).

Состояния игры принято называть узлами или позициями, а возможные выборы в каждой позиции – альтернативами. Окончательные позиции называются вершинами.

Характерной особенностью позиционной игры является возможность представления множества позиций в виде древовидного упорядоченного множества, которое называется деревом игры (Рис.1).

Рис.1

Символы О,А или В указывают, кто из игроков делает очередной ход в данной позиции (О – ход игры осуществляет «природа»).

Описание конечной игры двух лиц с помощью дерева, узлы которого соответствует ситуациям,в которых стороны осуществляют свои выборы, а вершины – ситуациям завершения операции, является моделью игры в позиционной или развернутой форме.

Цепь, связывающая начальную позицию с данной вершиной, называется партией.

Позиционная игра называется игрой с полной информацией, если в любой точке любой ее партии игрок, делающий ход, точно знает, в какой позиции он находится и какие выборы были сделаны ранее, а следовательно, из-за древовидности графа игры может восстановить и все предыдущие позиции. В графическом исполнении каждый узел такой игры будет представлять собой отдельное информационное множество, и поэтому в такой игре информационные множества пунктиром не отмечаются.

Теорема. В любой конечно-шаговой игре с полной информацией на конечном древовидном графе существует ситуация абсолютного равновесия по Нэшу.

Каждый ход игрока однозначно определяет последующую позицию дерева игры. В результате последовательного выбора позиций игроков однозначно реализуется некоторая последовательность узлов, определяющая путь в древовидном графе, исходящий из начальной позиции и достигающий одной из конечных вершин. Такой путь называется партией игры.

Разобьём все множество позиций дерева игры на три подмножества:

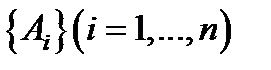- - множество очередности игрока А, т.е. множество позиций игрока А, в которых ему предоставлено право выбора очередной альтернативы. для наглядности будем изображать на дереве игры эти позиции кружками;

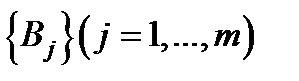- - множество очередности В, т.е. множество позиций игрока В, в которых ему предоставлено право выбора очередной альтернативы. для наглядности будем изображать на дереве игры эти позиции квадратами;

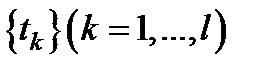- - множество конечных вершин, в которых задаются функции выигрышей игроков в виде: 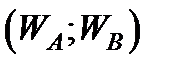(на первом месте стоит выигрыш игрока А в партии игры, определяемой данной вершиной, на втором – выигрыш игрока В). Для наглядности будем изображать на дереве игры конечные вершины овалами, в которых проставлены выигрыши игроков.

Ребра, выходящие из каждого узла, определяют альтернативы выбора на данном этапе. Поскольку выбор альтернативы в узле дерева игры эквивалентен выбору следующей позиции, будем считать, что стратегии указывают в каждой позиции номер ребра, по которому следует двигаться далее.

Дата добавления: 2017-01-13