Расчет коэффициента распыления изотропной мишени ионами инертных газов

ЦЕЛЬ РАБОТЫ

Изучить теоретические особенности ионно-плазменного распыл­ения и ме­тодику расчета коэффициента распыления изотропной ми­шени ионами инерт­ных газов.

1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

2.1. Ионное распыление

Физическим ионным распылением или просто ионным распылением назы­вается процесс удаления материала с поверхности в результате взаимодействия с ним энергетических ионов. Распыление впервые наблюдалось в 1852 году. Это явление первоначально было названо “катодным испарением”, поскольку материал катода “испарялся” при температурах существенно ниже температуры плавления материалов. Впоследствии утвердился термин “катодное распыле­ние”, так как на распыляемый материал - катод, подавался отрицательный элек­тричес­кий потенциал, ускоряющий в направлении его поверхности положи­тельные ионы. Однако этот термин определяет лишь ограниченный круг про­цессов ионного распыления. Распыление может проводиться предварительно сформированными и ускоренными до необходимых энер­гий пучками ионов без подачи на обрабатываемый материал отрица­тельного потенциала.

Развитие процесса ионного распыления с увеличением дозы ион­ной обра­ботки характеризуется двумя основными этапами. Первый этап - переходный, предравновесный. Он характеризуется постоянным ростом скорости распыле­ния. Происходит удаление поверхностных загрязнений, изменение рельефа по­верхности, ее структуры, энергии связей атомов на поверхности и, наконец, ус­тановление равновесной концентрации захваченных материалом ионов аргона. Второй этап - установившийся режим процесса ионного распыления. Распыля­ются собственно материал и внедренные в него ионы, концентрация которых установилась. Этот этап является основным в процессе распыления.

Современное представление о процессе взаимодействия, приводящего к распылению, предполагают, что в результате проникновения иона в материал возникает каскад бинарных упругих столкновений смещенных атомов, в которых происходит обмен энергией и импульса­ми между атомами. Среднее время развития каскада столкновений по­рядка c. Масса ионов должна быть достаточно велика, т.е. близка или больше массы атомов материала, чтобы увеличить вероятность смещения атомов в столкновениях, т.е. вероятность возникновения каскада столкновений. Конечным результатом каскада столкно­вений может стать передача поверхностному атому достаточной энер­гии и необходимого импульса нужной направленности (наружу из материала) для преодоления сил его связи на поверхности. Схема такого каскада представлена на рис.2.1. Если начало каскада нахо­дится глубоко от поверхности материала, то поверхностным атомам будет передана энергия, недостаточная для распыления. Таким обра­зом, энергия ионов определяет интенсивность процесса ионного рас­пыления.

Рис.2.1. Схема каскада упругих столкновений атомов А в мате­риале при ионной бомбардировке.

Ионное распыление материала начинается, когда энергия ионов пре­высит некоторую величину , получившую название порого­вой энергии распыления. Пороговую энергию можно определить из следующего выраже­ния:

(2.1)

где ; 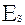- энергия сублимации материала (эВ); и -атомные массы иона и материала. слабо зависит от массы сталкивающихся частиц и лежит в диапазоне 10 - 30 эВ для ионов Ne,Ar, Кr и Хе. При ионы не распыляют материал, и при взаимодействии с атомарно-чистой поверхностью происходит их отражение, адсорбция с последующей десорбцией и нейтрализация, осуществляе­мая электронами, эмиттированными из материала под действием элек­трического поля ионов. Если на поверхности материала присутствуют адсорбированные инородные частицы и химические соединения, то в результате ионной бомбардировки происходит их десорбция и хими­ческие превращения (например, полимеризация).

Среднее расстояние, проходимое внедренным в материал ионом до его ос­тановки, зависит от энергии и атомного номера иона, а также атомного номера и кристаллической структуры материала. В боль­шинстве случаев важно знать не средний пробег ионов в материале, а среднюю глубину их проникновения от поверхности. Средняя глуби­на проникновения ионов аргона в диапазоне энер­гий (0,5 - 5,0 кэВ) составляет для кремния 3,5; для двуокиси кремния 5,0; для золота 1,3; для алюминия 1,5 нм/кэВ. Толщина нарушенного слоя приблизи­тельно равна удвоенной средней глубине проникновения ионов в ма­териал и возрастает с увеличением дозы ионного облучения. Основ­ная доля энергии ио­нов (70 – 90%) выделяется в материале в виде тепла, менее 5% расходуется на распыление, а оставшаяся часть затрачивается на радиационные повреждения материала, внедрение ионов, вторичную электронную эмиссию и электромаг­нитное излучение в широком спектре частот.

2.2. Коэффициент распыления

Для характеристики процесса ионного распыления используется параметр К, называемый коэффициентом распыления. Коэффициент рас­пыления определяется как количество распыленных атомов, приходящихся на один бомбардирующий ион (атом/ион). Когда состав распы­ленных частиц многоэлементный, например при распылении многоком­понентных материалов, для характеристики распыления используются парциальные (селективные) коэффициенты распыления отдельных ком­понентов или коэффициент распыления, выраженный в единицах моле­кула/ион. Для характеристики процесса распылени полимерных сое­динений типа фоторезистов, имеющих молекулы с очень большим чис­лом атомов, понятие коэффициента распыления теряет смысл, поскольку совершенно неопределенным становится состав продуктов распыления. В этом случае оперируют понятием скорости распыления, характеризующим толщину удаленного слоя материала в единицу вре­мени при заданной мощности ионной обработки. Скорость и коэффици­ент распыления связаны соотношением

(2.2)

гдее - заряд электрона, Кл; - плотность материала, ; - плотность тока ионов, 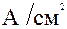; - масса атомов материала, г/моль; - число Аво­гадро, ; - скорость распыления, где h - толщина стравливае­мого слоя материала, см, a t - время распыле­ния, с.

Установлено, что эффективность процесса распыления определя­ется:

- зависимостью коэффициента распыления от характеристик бом­барди­рующих ионов: атомного номера, массы, энергии, направленнос­ти движения ионов по отношению к обрабатываемому материалу;

- от характеристик обрабатываемого материала: атомного номе­ра, массы, относительной плотности, энергии связи атомов, состав­ляющих материал, сте­пени кристалличности материала и состояния его поверхности;

- плотностью тока бомбардирующих ионов;

- влиянием среды: давления и состава остаточных и рабочих газов, нали­чием различного рода излучений и т.п.

Эффективность процесса ионного распыления в большей степени опреде­ляется энергией иона. С увеличением энергии К(Е) возраста­ет, достигает мак­симума, а затем уменьшается. В соответствии с представлениями о потерях энергии и пробеге ионов в материалах такой вид К(Е) достаточно легко объяс­ним. С увеличением энергии увеличивается поступление ее в обрабатываемый материал. Следова­тельно, растет доля энергии, передаваемой атомам на по­верхности. Однако одновременно растет глубина проникновения ионов в мате­ри­ал. Каскады столкновений, в результате которых энергия иона пере­дается на поверхность, начинаются на большей глубине, в процессе передачи энергии участвует большее числе ионов. Доля энергии, теряемой ионом в упругих столкновениях с атомами, уменьшается с увеличением энергии. В результате уменьшается энергия, которую получают атомы на поверхности. На рис. 2.2 представлен характер­ный вид зависимости коэффициента распыления серебра, меди и мо­либдена от энергии бомбардирующих ионов аргона К(Е).

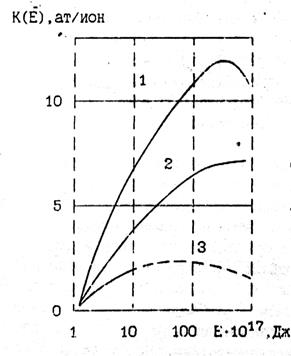
Рис.2.2. Зависимость коэф­фициентов распыления се­ребра (1), меди (2) и мо­либдена (3) от энергии ио­нов аргона

Практически у всех материалов с увеличением угла падения ионов от­носительно нормали к поверхности происходит увеличение коэффициента рас­пыления, затем достижение максимума и резкий спад до нуля. Подобную зави­симость изменения можно объяснить двумя причинами. С увеличением угла падения иона уменьшается глубина от поверхности, на которую он прони­кает в материал. Цепочки каскадных столкновений, в результате которых рас­пыляются атомы на поверхности, развиваются вблизи поверхности материала и они более короткие. Следовательно, повышается вероятность передачи атомам на поверхности энергии, достаточной для распыления. В то же время при слишком больших углах падения иона возрастает вероятность его обратного рассеяния без проникновения в материал. С другой стороны, зависимость определяется изменением поперечного се­чения взаимодействия иона с атомом. Более сильная зависимость наблюдается у материалов с боль­шей энергией связи атомов на поверхности, т.е. у материалов с низким коэф­фициентом_распыления.

Рис.2.3.Зависимость относи­тельных коэффициентов рас­пыления кремния от угла па­дения при различных энергиях ионов аргона:

1-1 кэВ; 2 - 0.5 кэВ; 3 -0.35 кэВ

Вероятность взаимодействия иона с атомом определяется сечением взаимодей­ствия иона с атомом. Материалы с высоким коэффициентом распыления имеют атомы с заполненными d-электронными оболочками, т.е. с большим сечением взаимодействия. При изменении угла паде­ния “прозрачность” атомов легко распыляемого материала изменяется мало. У плохо распыляемых материалов “прозрачность” атомов значи­тельно уменьшается за счет увеличения сечения взаимодействия при увеличении угла падения иона на поверхность материала. На рис.2.3 представлена зависимость относительных коэффициентов распыле­ния кремния от угла падения при различных энергиях ионов аргона.

Зависимость коэффициента распыления от вида бомбардирующего иона характеризуется ростом его с увеличением атомного номера и массы иона, на­блюдается тенденция к насыщению в этой зависимости.

Зависимость коэффициентов распыления от атомного номера ма­териала носит периодический характер, причем периоды изменения К материалов соот­ветствуют периодам таблицы Д.И.Менделеева. Макси­мальные коэффициенты распыления имеют материалы, состоящие из атомов побочной подгруппы 1-й группы периодической системы: медь, серебро, золото. Отличительной особен­ностью этих атомов является целиком заполненная d-электронная оболочка. Можно считать, что степень заполнения d-оболочки атома электронами опре­деляет распыляемость материалов.

Коэффициент распыления с изменением температуры обрабатывае­мого материала практически не меняется. Отсутствие зависимости К(Т) показывает, что увеличение поперечного сечения взаимодейс­твия незначительно с увеличе­нием температуры. Сечение взаимодейс­твия определяется скоростью быстрой частицы, участвующей во взаи­модействии, а именно скоростью бомбардирую­щего иона. По сравне­нию с ионом атом обрабатываемого материала можно считать покоя­щимся независимо от его температуры. В то же время нельзя счи­тать, что температура не оказывает какого-либо влияния на процесс ионного распыления. Она в сильной степени может влиять на состоя­ние поверхности и состав распыляемого материала, на процессы ад­сорбции, десорбции остаточ­ных газов на поверхности, на степень кристаллического совершенства припо­верхностного слоя материала, в котором происходит смещение атомов в ре­зультате ионной бомбарди­ровки. Влияние температуры проявляется также в изменении коли­чества распыленных возбужденных и ионизированных частиц.

2.3. Методика расчета коэффициента распыления

2.3.1.Для описания распыления предложено несколько моделей, предпола­гающих два основных механизма процесса. Согласно первому, распыленные атомы возникают в результате сильного локального ра­зогрева поверхности ма­териала в месте падения иона. Согласно второму - передача энергии и импульса бомбардирующего иона атомам материала вызывает каскады упругих столкно­вений, смещенных из своих равновесных состояний атомов, результатом кото­рых становится распыление. Возможен третий механизм - химическое разложе­ние обрабатываемого ионами материала на летучие компоненты. Некоторые закономерности распыления могут быть объяснены с помощью тепловой мо­дели. В тепловой модели “горячего пятна” пред­полагается, что энергия бом­бардирующей частицы выделяется в малой области, порядка нескольких атом­ных радиусов, вблизи места паде­ния иона на поверхность. Температура в этой области резко возрас­тает, и с нагретого участка поверхности происходит испа­рение атомов. Другая тепловая модель - модель “теплового клина” - предпо­ла­гает, что локальный разогрев создается быстрыми вторичными частицами, об­разующимися при взаимодействии иона с материалом. Первичный смененный атом, двигаясь в материале, быстро теряет свою энергию, передавая ее сосед­ним атомам. Процесс “остывания” групп атомов может быть описан с помощью классической теории теплопро­водности. Размер “теплового клина” порядка см.

В импульсных теориях предполагается, что основные потери энергии иона определяются ядерным торможением в приповерхностном слое материала ог­раниченной толщины. Электронным торможением пренебрегают.

Расчет коэффициента распыления - основного параметра процес­са ионного распыления - проводится на основании представления о беспорядочном тормо­жении иона в беспорядочной среде.

Рассчитываются потери энергии ионов в материале; число пер­вичных и вторичных смененных атомов; число смещенных атомов, дос­тигающих по­верхности; число атомов, обладающих достаточной энер­гией для преодоления сил связи на поверхности.

В основу методики расчета коэффициента распыления положен метод, предложенный В.Юдиным [3]. Он существенно упрощает проце­дуру расчетов при разработке технологических циклов ионной и ионно-плазменной обработке широкого класса материалов.

2.3.2.Рассчитывается радиус экранирования ядра электронной оболочкой, сечение экранирования, нормирующий множитель энергии тона:

(2.3)

(2.4)

(2.5)

где - радиус Бора; , 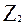и, , - атомные номера и массы ускоренного иона (1) и атома мишени (2).

2.3.3. Вычисляются безразмерное значение энергии сублимации и энергия максимума иона, соответствующая максимальному значению коэффициента распыления:

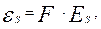(2/6)

(2.7)

где 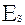- энергия сублимации материала, эВ.

2.3.4. Определяется коэффициент, учитывающий периодические осцилля­ции коэффициента распыления в зависимости от расположения элемента в пе­риодической таблице элементов Д.И.Менделеева:

при

при 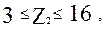(2.8)

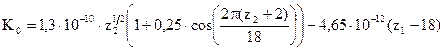
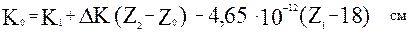при .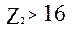

Значения постоянных , и приведены в табл.2.1.

Таблица 2.1

Диапазон	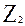, см	, см
19 – 25	5,8	1,0	19
26 – 31	3,38	11,1	26
32 – 46	8,5	0,72	32
47 – 48	9,8	14,0	47
49 – 61	12,4	- 3,5	49
62 – 69	8,0	8,33	62

2.3.5. Находится значение максимального коэффициента распыления

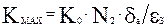ат/ион, (2.9)

где - собственная конценрация атомов в материале мишени, .

2.3.7. Строится зависимость К(Е), используя данные табл.2.2 и выражение для коэффициента распыления

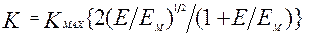. (2.10)

Таблица 2.2

0,001

0,003

0,01

0,03

0,1

0,3

1

3

10

30

100

3. ВЫПОЛНЕНИЕ РАБОТЫ

3.1. Для заданного иона инертного газа (Ne, Ar, Кr, Хе) и материала ми­шени (см. приложение) найти значение пороговой энер­гии .

3.2. Произвести расчет коэффициента распыления согласно пункту 2.3.

3.3. Построить график зависимости коэффициента распыления от энергии бомбардирующего иона K(E).

3.4. Определить время, в течение которого будет удален слой материала толщиной 1 мкм. Плотность тока j принять равной , где N - номер варианта. Расчет производить.для максималь­ного значения коэффици­ента распыления. Учесть, что величина определяется следующим выраже­нием: .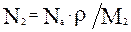

ПРИМЕЧАНИЕ. Nе: = 10, = 20,1; Ar: = 18, = 39,9; Kr: = 36, = 83,8; Xe: = 54, = 131,3.

4.КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Современные представления о процессе распыления.

2. Пороговая энергия распыления.

3. Характерные этапы процесса ионного распыления.

4. Связь между скоростью и коэффициентом распыления.

5. Зависимость коэффициента распыления от энергии и вида.иона, угла па­дения, атомного номера и температуры материала мишени.

6. Методика расчета коэффициента распыления.

7. Какими параметрами определяется эффективность процесса распыле­ния.

8. Модели механизма ионного распыления материалов.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Ивановский Г.Ф., Петров В.И. Ионно-плазменная обработка материалов. М.: Радио и связь. 1986. 232 с.

2. Данилин Б.С. Применение низкотемпературной плазмы для на­несения тонких пленок. М.: Энергоатомиздат, 1989. 328 с.

3. Юдин В.В. Коэффициент распыления изотропных мишеней// Электрон­ная техника. Сер. 2. 1984. Вып. 6(172). С. 3 - 16.

4. Попов В.Ф., Горин Ю.Н. Процессы и установки электрон­но-ионной тех­нологии. М.: Высшая школа. 1988. 255 с.

5. Фундаментальные и прикладные аспекты распыления твердых тел. М.: Мир, 1989. 349 с.

ПРИЛОЖЕНИЕ

Таблица П.1

Дата добавления: 2017-01-13