Пример 4.4.3-3. Написать процедуру-Function, которая присваивает переменной f наибольшее из значений двух переменных x и y

Пример 4.4.3-2. Написать процедуру, вычисляющую x

Sin(a²) + b, если, а> b;

x =

a – b, в противном случае.

Данную задачу можно решить двумя способами. На рис 4.4.3-7 при­ведена схема алгоритма решения задачи, в которой использовано стан­дартное разветвление, а на рис.4.4.3-8 – усеченное разветвление. Второй способ в данном случае предпочтительнее, поскольку упрощает про­граммную реализацию алгоритма. Усеченное разветвление реко­мендуется использовать в тех случаях, когда выбор из двух возможных ветвей производится последовательно и неоднократно.

Function Pr437(ByRef a As Double _ ByVal b As Double) As Double Dim x As Double If a > b Then x = Sin(a^2) + b Else x = a – b End If Return x End Function

Рис. 4.4.3-7. Схема алгоритма и программный код процедуры Pr437()
проекта Пример 4.3-2

Function Pr438(ByVal a As Double_ ByVal b As Double)As Double Dim x As Double x = a – b If a > b Then x = Sin(a^2) + b Return x End Function

Рис. 4.4.3-8. Схема алгоритма и программный код процедуры Pr438()
проекта Пример 4.3-2

Процедура - Function Pr437() или Pr438() может быть вызвана, например, как на рис. 4.4.3-9.

Dim XX, aa, bb As Double aa= vvodDbl2("Ввод a=", TextBox1) bb= vvodDbl2("Ввод b=", TextBox2) XX=Pr438(aa, bb) vivodDbl2(XX,"Значение функции ", TextBox3)

Рис. 4.4.3-9. Пример вызова процедуры Pr438()

проекта Пример 4.3-2

Function Pr4310(ByVal x As Double_ ByVal y As Double) As Double Dim f As Double If x > y Then f = x Else f = y Return f End Function

Рис. 4.4.3-10. Схема алгоритма и программный код процедуры Pr4310()
проекта Пример 4.3-3

Алгоритмы и программы решения задачи вы­бора наибольшего из двух значений приведены на рис.4.4.3-11 и 4.4.3-12.

Function Pr4311(ByVal x As Double_ ByVal y As Double) As Double Dim f As Double f = x If y > f Then f = y Return f End Function

Рис. 4.4.3-11. Схема алгоритма и программный код процедуры Pr4311() проекта Пример 4.3-3

В первом способе (рис. 4.4.3-10) используется стандартное разветвление, а во втором (рис.4.4.3-11) – усеченное.

Процедура- Function Pr4310() (или Pr4311()) может быть вызвана, например, как на рис. 4.4.3-12.

Обратите внимание, что:

If x > y Then f=x Else f=y соответствует функции f = max{x, y}, а

If x < y Then f=x Else f=y с оответствует функции f = min{x, y },

где x и y любые арифметические выражения.

Dim ff As Double Dim xx, yy As Double xx= vvodDbl2("Ввод x=", TextBox1) yy= vvodDbl2("Ввод y=", TextBox2) ff=Pr4311(xx, yy) vivodDbl2(ff, "max{x, y }= ", TextBox3)

Рис. 4.4.3-12. Пример вызова процедуры Pr4311()

проекта Пример 4.3-3

Пример 4.4.3-4. Написать процедуру-Function, которая вычисляет r = min{ a+b, c², }.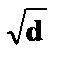

Function Pr4313(ByVal a As Double_ ByVal b As Double_ ByVal c As Double _ ByVal d As Double) As Double Dim min As Double min = a + b If c^2 < min Then min = c^2 If Sqrt(d) < min Then min = Sqrt(d) Return min End Function

Рис. 4.4.3-13. Схема алгоритма и программный код процедуры Pr4313() проекта Пример 4.3-4

Решение задач выбора наибольшего (наименьшего) из значений переменных или выражений числом более двух сводится к последовательному применению усеченных разветвлений.

Алгоритм, реализующий Пример 4.4.3-4 (рис.4.4.3-13), относится к числу базовых алгоритмов выбора наименьшего из нескольких значений. Основой алгоритма является усеченное разветвление. Здесь первоначально переменной min присваивается значение первого из выражений. Истинное значение наименьшего значения определяется путем последовательного сравнения со всеми остальными значениями выражений заданной последовательности.

Процедура- Function Pr4313() может быть вызвана, как на
рис. 4.4.3-14.

Dim rr As Double Dim aa, bb, cc, dd As Double aa = vvodDbl2("Ввод a=", TextBox1) bb = vvodDbl2("Ввод b=", TextBox2) cc = vvodDbl2("Ввод c=", TextBox3) dd = vvodDbl2("Ввод d=", TextBox4) rr = Pr4313(aa, bb, cc, dd) ivodDbl2(rr,"Значение min = ", TextBox5)

Рис. 4.4.3-14. Пример вызова процедуры Pr4313() проекта Пример 4.3-4

Пример 4.4.3-5. Написать процедуру-Function, которая вычисляет значение функции y(x) в соответствии со следую­щим правилом:

e^x, если x<=-1;

y(x)= 3, если x>1;

2, если –1<х≤1.

Function Pr4315(ByVal x As Double)_ As Double Dim y As Double If x <= -1 Then y = Exp(x) ElseIf x > 1 Then y=3 Else y=2 End If Return y End Function

Рис. 4.4.3-15. Схема алгоритма и программный код процедуры Pr4315()

Процедура - Function Pr4315() может быть вызвана, например, как на рис. 4.4.3-16.

Dim YY As Double Dim x As Double x= vvodDbl2("Ввод x=", TextBox1) YY=Pr4315(x) vivodDbl2(YY,"Значение функции ", TextBox2)

Рис. 4.4.3-16. Пример вызова процедуры Pr4315()

проекта Пример 4.3-5

Пример 4.4.3-6. Даны действительные числа x0, y0. Определить принадлежит ли точка с координатами (x0, y0) геометрической фигуре: ромб с вершинами в точках (0, 1), (1, 0), (0, -1), (-1, 0).

На этапе формализации задачи, прежде всего, построим заданную геометрическую фигуру (рис. 4.4.3-17).

Рис. 4.4.3-17. Ромб с вершинами в точках (0, 1), (1, 0), (0, -1), (-1, 0)

Известно, что ax+by=c – это уравнение прямой, а ax+by≤c и ax+by≥c – это два множества, одно из которых лежит над прямой (включая точки этой прямой), а другое под этой прямой. Для того чтобы выяснить, какое из неравенств надо взять, необходимо подставить координаты любой точки
M(x₁, y₁) в это неравенство (лучше взять точку M(0, 0), чтобы упростить вычисления).

Если ее координаты удовлетворяют этому неравенству, значит, эта точка M принадлежит указанному множеству, в противном случае – нет. Запишем уравнения прямых AB, BC, CD, DA:

AB: x-y=-1; BC: x+y=1; CD: x-y=1; DA: x+y=-1.

Таким образом, для того чтобы точка M₀(x₀, y₀) принадлежала замкнутой заштрихованной области, необходимо выполнить следующие условия:

.

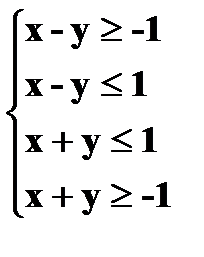
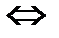
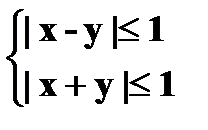Разобьем решение задачи на несколько отдельных этапов и создадим процедуры пользователя, реализующие эти задачи:

1) Процедуру-подпрограмму Resh(), которая возвращает строку с ответом на вопрос, принадлежит ли точка с передаваемыми через параметры координаты заданной геометрической фигуры.

2) Процедуру-функцию vvod() для ввода действительного числа из TextBox.

3) Процедуру-подпрограмму vivod() для вывода строки в TextBox.

4) Событийную процедуру, которая должна содержать вызовы всех разработанных процедур.

5) Программный код решаемой задачи представлен на рис. 4.4.3-18.

Option Strict On Option Explicit On Imports System.Math Public Class Form1 'Функция ввода значения вещественного типа из TextBox Function vvod(ByVal T As TextBox) As Double Return CDbl(T.Text) End Function 'Процедура вывода результата в TextBox Sub vivod(ByVal Z As String, ByRef T As TextBox) T.Text = Z End Sub ' Процедура решения задачи Sub Resh(ByVal x0 As Double, ByVal y0 As Double, _ ByRef z As String) If Abs(x0 - y0) <= 1 And Abs(x0 + y0) <= 1 Then z = "Точка принадлежит фигуре" Else z = "Точка не принадлежит фигуре" End If End Sub Private Sub Button1_Click(sender As Object, e As EventArgs) _ Handles Button1.Click Dim x, y As Double Dim z As String x = vvod(TextBox1): y = vvod(TextBox2) Resh(x, y, z): vivod(z, TextBox3) End Sub End Class

Рис. 4.4.3-18. Программный код проекта Пример 4.3-6

Пример 4.4.3-7. Задано число n. Если n – натуральное нечетное число, меньше 10, то целочисленной переменной f присвоить 1, если n – натуральное четное число, то переменной f присвоить 2, если n – отрицательное, то присвоить f значение -1, если значение n находится внутри отрезка [10;1000], то f присвоить 10, иначе f присвоить 0.

Function Pr4319(ByVal n As Integer) As Integer Dim f As Integer Select Case n Case 1, 3, 5, 7, 9 f =1 Case 2, 4, 6, 8 f =2 Case Is <0 f =-1 Case 10 TO 1000 f =10 Case Else f =0 End Select Return f End Function

Рис.4.4.3-19. Программный код процедуры Pr4319()

Проекта Примера 4.4.3-7

Программный код решения Примера 4.4.3-7 с использованием оператора Select Case приведены на рис.4.4.3-19.

Процедура- Function Pr4319() может быть вызвана из любой другой процедуры или из модуля формы, например, как на рис. 4.4.3-20.

Dim ff As Integer Dim nn As Integer nn= vvodInt4(TextBox1) ff=Pr4319(nn) vivodInt4(ff, TextBox2))

Рис. 4.4.3-20. Пример вызова процедуры Pr4319()

Проекта Примера 4.3-7

Дата добавления: 2017-01-13