Основные задачи при изучении статистических рядов динамики

Статистические ряды динамики

Ряд динамики – ряд расположенных во времени уравнений каких-либо показателей, которые в своих последних суммах характеризуют ход развития изученного общего явления, изменяется во времени и характеризуется абсолютными средними или относительными величинами.

Любой ряд динамики состоит из двух элементов, в каждой графе ряда указываются моменты, например, на первое число, или же интервалы времени, к которым относятся приводимые в ряду статистические данные характеризующие изученные общие явления на тот момент или за тот период времени, который указан в данной графе изученного ряда динамики. В зависимости от характера явлений и сущности отражаемых статистических показателей различают три вида рядов динамики:

· Вид А – ряды абсолютных величин

· Вид В – Ряды средних величин

· Вид С – Ряды относительных величин

Для рядов абсолютных величин характерно дальнейшее деление на моментные ряды динамики и интервальные ряды динамики.

Моментные ряды динамики представляют собой ряды абсолютных величин, характеризующих уровень изучаемого общественного явления на определенный момент времени. Пример: экономическая деятельность на территории РК характеризуется следующими данными (таблица 1).

Таблица 1

Среднегодовая численность занятых в экономике РК

Годы
Численность занятых, тыс. чел.	507,8	569,3	628,6	664,3	675,8	545,5	499,2	504,7	510,3	521,4

Данный ряд называется моментным, потому что данные им уровни относятся к моментам времени на 31 декабря соответствующего года в 24⁰⁰.

Интервальные ряды динамики представляют собой ряды абсолютных величин, которые характеризуют уровень изучаемого общественного явления за какой-то период времени. Пример: социальная жизнь в РК за 1990-2003 гг. характеризуется следующими данными (таблица 2).

Таблица 2

Число зарегистрированных преступлений в РК по видам (ед)

Годы
Зарегистрированные преступления, ед

Данный ряд называется интервальным, потому что уровень 1990г, напрямую относится к периоду с 00⁰⁰ 1 января 1990г по 24⁰⁰ 31 декабря 1990г, что одновременно соответствует 00⁰⁰ 1 января 1991г.

Особенностью интервальных рядов динамики является то, что данные этих рядов можно суммировать и получать новые статистические данные, имеющие реальное содержание. В противоположность сумма чисел моментного ряда динамики не отвечает никакому реальному содержанию, и накопленные итоги для этих рядов не рассчитываются.

Вышесказанное позволяет различать ряды данного вида на практике.

1. Определение среднего уровня ряда.

2. Измерение отдельных изменений в уровнях ряда.

3. Выявление закономерности динамики ряда, т.е. закономерностей изменения уровней ряда во времени.

4. Раскрытие факторов, обуславливающих изменение изученного общественного явления.

Примем следующие обозначения:

· t – момент (период) времени, к которому относятся статистические данные.

· y – уровень ряда или средняя абсолютная относительная величина, характеризующая изучаемое явление на определенный момент или за определенный период времени и относящаяся к составленному периоду времени.

Пусть нам даны периоды или моменты времени t₀; t₁; t₂...….t_n и относящиеся к ним уровни ряда y₀; y₁; y₂…….y_n, где t₀ и t_n соответственно начальный и конечный момент либо период времени, а y₀ и y_n соответственно начальный и конечный уровни ряда, тогда для данного ряда динамики при принятых обозначениях могут быть рассчитаны следующие показатели:

1. Средний уровень ряда динамики, рассчитанный для интервального ряда по формуле (1а) или по формуле средней арифметической простой

(1а)

Для моментного ряда динамики средний уровень рассчитывается по формуле средней хронологической (1б)

(1б)

2. Средний абсолютный прирост или снижение показывает, насколько абсолютных единиц увеличивается или уменьшается данный уровень ряда по сравнению с уровнем, принятым за базу сравнения.

Расчет большей части показателей динамических рядов основан на сравнении между собой уровней ряда динамики, когда уровень, с которым производится сравнение, называется базисным, т.к. он является базой сравнения. Обычно, за базу сравнения принимают либо начальный, либо предыдущий уровень ряда динамики. Если уровень сравнивают с предыдущим, то полученные при этом показатели носят название цепных показателей. Если же все уровни сравниваются с каким-то одним уровнем, выступающим в качестве постоянной базы сравнения, то полученные при этом показатели носят название “базисные”. Отсюда, средний абсолютный прирост может быть рассчитан, как

, (2)

где - базисный абсолютный прирост

n – число уровней ряда в период, за который произошло увеличение или уменьшение данного показателя.

3. Цепной абсолютный прирост рассчитывается по формуле

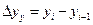, (3)

4. Базисный абсолютный прирост по формуле:

(4)

· y_i – сравниваемый уровень ряда

· y_i-1 – предыдущий уровень ряда

· y₀ – базисный уровень или уровень принятый за постоянную базу сравнения

· y₀ – const

5. Коэффициент роста или снижения показывает, во сколько раз увеличивается или уменьшается данный уровень ряда по сравнению с уровнем, принятым за базу сравнения. В зависимости от базы сравнения коэффициенты роста или снижения могут быть также цепными (1) и базисными (2):

Между цепным и базисным коэффициентами роста существует определенная взаимосвязь. Если динамические ряды приведены за один и тот же период времени, тогда произведение цепных индексов или коэффициентов роста равно соответствующему базисному индексу или коэффициенту роста. Если же разделить последний базисный индекс или коэффициент роста на предыдущий, то в результате получится соответствующий цепной индекс или коэффициент роста.

6. Коэффициент прироста показывает, на сколько относительных единиц увеличивается или уменьшается уровень ряда по сравнению уровнем, принятым за базу сравнения. В самом общем виде коэффициент прироста рассчитывается как (5), формула для цепного коэффициента прироста имеет вид (5а), а для базисных (5б):

7. Темп роста или снижения Т показывает, сколько % сравнительный уровень составляет по отношению к другому уровню, принятому за базу сравнения, и численно равен коэффициенту роста, выраженному в процентах:

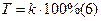
Для цепных формула (6) имеет вид (6а), для базисных (6б)

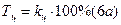
8. Темпы прироста показывают на сколько процентов увеличивается или уменьшается данный уровень ряда по сравнению с уровнем, принятым за базу сравнения и вычисляется по формулам:

Дата добавления: 2017-01-13