Методические указания к решению задачи №1

Решение задачи

1. Выбор типа решаемой задачи: Preferences -> Structural
2. Задание параметров: Parameters -> Scalar parameters
3. Выбор конечного элемента: Preprocessor -> Element type -> Add/Edit/Delete

Элемент BEAM189 – стержневой конечный элемент

Элемент SHELL93 – оболочечный конечный элемент

1. Задание реальных констант для элемента SHELL93: Preprocessor -> Real Constant -> Add/Edit/Delete

1. Выбор сечения: Preprocessor -> Sections -> Beam -> Common Sections

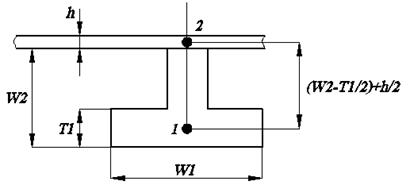
1. Свойства материала: Preprocessor -> Material props -> Material models
2. Построение точек по координатам: Preprocessor -> Modeling -> Create -> Keypoints ->In Active CS

1. Пользовательская система координат: WorkPlane ->Local Coordinate Systems> Create Local CS> At WP Origin

1. Построение линии в активной системе координат: Preprocessor -> Modeling -> Create -> Lines -> Lines -> In Active CS
2. Декартовая система координат: Workplace -> Change Active CS -> Global Cartesian
3. Построение прямых линий: Preprocessor -> Modeling -> Create -> Lines -> Lines -> in Active CS
4. Протяжка линии вдоль линии: Preprocessor -> Modeling -> Operate -> Extrude -> Lines -> Along Lines

1. Слияние двойных элементов: Numbering Ctrls -> Merge Items
2. Перенумерация: Numbering Ctrls -> Compress Number

1. Построение ориентационных точек копированием: Preprocessor -> Modeling -> Copy -> KeyPoints ->

1. Разбиение на конечные элементы: Preprocessor -> Meshing -> Mesh Tools

1. Закрепление по линиям: Solution -> Define Loads -> Apply -> Structural -> Displacement -> On Lines

1. Градиент нагрузки: Solution -> Define Loads -> Settings -> For Surface Ld -> Gradient ->

1. Приложение давления: Solution -> Define Loads -> Apply -> Structural -> Pressure -> On Areas

20. Запуск программы на счет: Solution -> Solve -> Current LS

Результаты расчета:

Максимальное перемещение:

Максимальное напряжение:

Перед решением задачи необходимо изучить теоретический материал. Сущность метода заключается в том, что наивероятнейшими значениями аргументов искомой аналитической зависимости будут такие, при которых сумма квадратов отклонений экспериментальных значений функции от самой исследуемой функции будет наименьшей:

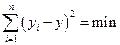
Искомая функциональная зависимость имеет линейный характер

y=a+bx

График функции представляет прямую линию с коэффициентом b=tga, пересекающая ось ординат в точке y=a

В соответствии с методом наименьших квадратов искомым постоянным соответствует минимальное значение выражения:

Можно показать:

В соответствии с этими формулами необходимо вычислить:

1. Постоянные коэффициенты a и b по формулам 1.34. Предварительно вычислив S₁, S₂, S₃, S₄, S₅ по формулам 1.35, где x_i – T_i, y_i -Δ L_i, n= 7 – количество экспериментов.

2. Построить теоретический график зависимости приращение длины ΔL от температуры и нанести на него экспериментальные точки.

3. Вычислить среднеквадратичное отклонение погрешности измерения длины по формуле 1.37

4. Вычислить среднеквадратичное отклонение найденных значений а и b по формулам 1.36

Задача №2

Для оценки влияния случайных погрешностей на стабильность технологического процесса шлифования роликов провели 100 последовательных измерений диаметров роликов в пределах 20,00 до 20,35 мм и разбили на семь интервалов. Распределение количества роликов по интервалам (частота m) приведено в табл.2. Вариант выбрать по последней цифре шифра. Построить гистограмму распределения измеренных диаметров. Определить среднее квадратичное отклонение измерений диаметров роликов. Построить кривую нормального распределения Гаусса, соответствующую вычисленному значению среднего квадратичного отклонения. Установить вероятность работы без брака при допуске на диаметр .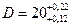

шифр
Интервал, мм	Частота, m
20,0 – 20,05
20,5 – 20,10
20,10 – 20,15
20,15 – 20,20
20,20 – 20,25
20,25 – 20,30
20,30 – 20,35
Итого n=Σm:

Перед решением задачи изучить теоретический материал по учебнику Я.М. Радкевич и др. Метрология, стандартизация и сертификация. М. «Высшая школа» 2007. с. 36-66.

Дата добавления: 2017-01-13