Матвиенко В.А. 2 страница

,

которое равно среднему полупериодному значению

.

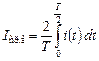Действующее значение периодического колебания равно среднему квадратическому значению за период колебания

.

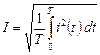Поскольку мощность пропорциональна квадрату тока, то очевидно, что действующее значение периодического тока равно постоянному току, который эквивалентен по выделяемой мощности. Номинальные токи и напряжения электротехнических устройств определяются, как правило, действующими значениями.

Для характеристики формы периодических колебаний используют такие понятия как коэффициент формы

и коэффициент амплитуды

.

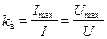Эти коэффициенты чаще всего используют в электроизмерительной технике для пересчета показаний приборов.

1.6. Среднее, средневыпрямленное и действующее значения
гармонического колебания

Найдем среднее значение гармонического тока :

.

Но . Тогда

.

Принимая во внимание, что , получим

.

Этот результат может быть получен сразу из геометрического смысла определённого интеграла.

Найдем средневыпрямленное значение гармонического тока, которое равно среднему полупериодному значению:

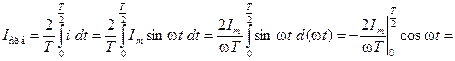
Найдем действующее значение гармонического тока

.

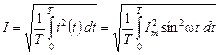Учитывая, что или , получим

.

Но . Тогда действующее значение гармонического тока

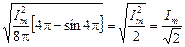= ≈ 0,707 I_m.

Коэффициент амплитуды гармонического колебания

k _а = ≈ 1,41.

Коэффициент формы гармонического колебания

k _ф = ≈ 1,11.

Если действующее значение гармонического напряжения U = 220 В, то амплитуда гармонического напряжения U_m = 1,41 U =
= 311 В, а средневыпрямленное значение =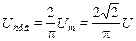
= 0,900 U =198 В.

1.7. Спектральное представление периодических сигналов

Как известно из курса математики, любая периодическая функция, удовлетворяющая условиям Дирихле (т. е. кусочно-монотонная и ограниченная на отрезке [ ‑π, π]), может быть представлена рядом Фурье.

Пусть периодический сигнал s (t) с периодом T отвечает условиям Дирихле. Тогда он может быть представлен рядом Фурье

,

коэффициенты которого a ₀, a_n и b_n определяются по формулам:

,

,

.

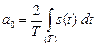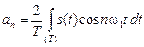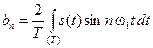Частоту называют основной частотой.

Итак, в общем случае периодический сигнал содержит постоянную составляющую и бесконечный ряд гармонических колебаний (гармоник), частота которых кратна основной частоте.

Каждую гармонику можно описать ее амплитудой A_n и начальной фазой ψ _n:

,

где

, .

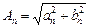С учетом этих соотношений ряд Фурье можно представить в следующем виде:

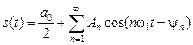. (1.1)

Совокупность амплитуд A_n, отложенных в функции частоты, образует амплитудную спектральную диаграмму сигнала s (t) (рис. 1.15). Совокупность начальных фаз ψ _n, отложенных в функции частоты, образует фазовую спектральную диаграмму сигнала s (t) (рис. 1.16). Амплитудный и фазовый спектры периодического сигнала являются линейчатыми или дискретными. В зависимости от формы сигнала s (t) амплитуды некоторых гармоник могут быть равны нулю.

Представим ряд Фурье в комплексной форме записи, для чего распишем косинус в выражении (1.1) по формуле Эйлера. Получим

.

В последнем выражении каждую из экспонент запишем в виде произведения двух экспонент. Тогда

.

Но есть не что иное, как комплексная амплитуд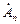а , а 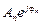‑ величина ей комплексно сопряженная :

.

Знак минус в показателе экспоненты можно отнести к номеру гармоники n. Полагая, что постоянная составляющая сигнала s (t) представляет собой нулевую гармонику (n = 0), окончательно находим

.

Получим формулу для вычисления коэффициентов комплексного ряда Фурье

.

Подставим выражения для коэффициентов ряда Фурье

.

Распишем косинус и синус по формулам Эйлера:

.

Каждый из интегралов представим в виде алгебраической суммы двух интегралов:

.

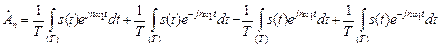После приведения подобных членов окончательно получим:

.

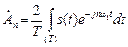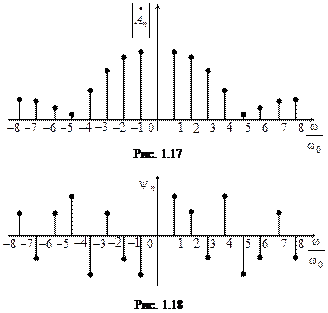Амплитудный спектр, соответствующий комплексному ряду Фурье, симметричен относительно нулевой частоты (рис. 1.17), а фазовый спектр симметричен относительно начала координат (рис. 1.18).

1.8. Спектральное представление непериодических сигналов

Пусть периодический сигнал s (t) представляет собой одиночный импульс произвольной формы, заданный на отрезке [ t ₁, t ₂], за пределами которого s (t) = 0 (рис. 1.19). Чтобы непериодическую функцию s (t) можно было представить рядом Фурье, доопределим ее так, чтобы она стала периодической. Полученную периодическую функцию s _пер(t) можно представить рядом Фурье

,

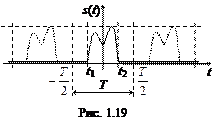
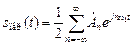коэффициенты которого

.

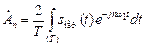Умножим и разделим каждый член ряда Фурье на πω₁. Тогда ряд Фурье можно записать в виде

.

По определению основная частота . Тогда .

Выражение в квадратных скобках представляет собой частотный интервал между составляющими ряда Фурье, равный частоте повторения ω₁:

.

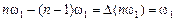С учетом сказанного ряд Фурье можно переписать в следующем виде:

.

Подставим выражение для :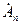

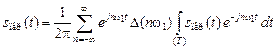. (1.2)

Но исходная функция s (t) равнялась нулю всюду, за исключением отрезка времени [ t ₁, t ₂], а функция s _пер(t) отлична от нуля не только на отрезке [ t ₁, t ₂]. Чтобы вернуться к исходной непериодической функции s (t), устремим период T функции s _пер(t) к бесконечности.

При T → ∞:

· периодическая функция s _пер(t) стремится к исходной непериодической функции s (t);

· модули комплексных амплитуд гармоник 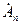уменьшаются, стремясь к нулю: ;

· частотный интервал между линиями спектра уменьшается, стремясь к нулю, , т. е. дискретный спектр превращается в сплошной;

· .

Функцию

(1.3)

называют спектральной плотностью, спектральной характеристикой или просто спектром непериодической функции s (t);

· операция суммирования в выражении(1.2) превращается в операцию интегрирования.

Итак, при T → ∞ получим:

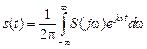. (1.4)

Преобразование, определяемое формулой (1.3), называют прямым двухсторонним преобразованием Фурье. Прямое преобразование позволяет перейти от представления сигнала во временной области s (t) к его представлению в частотной области S (j ω).

Преобразование, определяемое формулой (1.4), называют обратным преобразованием Фурье. Оно позволяет перейти от представления сигнала в частотной области S (j ω) к его представлению во временной области s (t). Оба представления сигнала (временное и спектральное) несут полную информацию о сигнале и в этом смысле являются эквивалентными.

Согласно обратному преобразованию Фурье непериодический сигнал s (t) представляет собой совокупность бесконечной суммы гармоник с бесконечно малыми амплитудами во всем диапазоне частот от ‑ ∞ до + ∞.

Рассмотрим соотношение между спектрами одиночного импульса и периодической последовательности импульсов такой же формы, для чего сравним выражение для спектральной плотности одиночного импульса с выражением для комплексной амплитуды n -ой гармоники соответствующего периодического колебания:

,

.

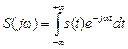В точках ω = n ω₁

.

Из сопоставления S (j ω) и 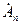следует, что

,

т. е. модуль спектральной плоскости одиночного импульса и огибающая линейчатого спектра периодической последовательности импульсов той же формы, совпадают по форме и отличаются только мас
штабом (множитель 2/ Т) (рис. 1.20).

1.9. Единичные функции и их свойства

Рассмотрим сигнал, описывающий линейный переход из нулевого состояния в единичное за время Δ t (рис. 1.21) Если параметр Δ t устремить к нулю, то в пределе переход от нулевого состояния в единичное будет происходить мгновенно (рис. 1.22). Такой предельный сигнал называют единичным скачком, функцией включения или функцией Хевисайда (Оливер Хевисайд, английский физик, 1850 – 1925 г.).

Математическая модель функции включения имеет вид:

1(t) = 0, t < 0;
1(t) = 1, t ≥ 0.

В общем случае функция включения может быть смещена относительно начала отсчета времени на величину t ₀ (рис. 1.23). В аналитическом виде смещенную функцию включения можно записать следующим образом:

1(t – t ₀) = 0, t < t ₀;
1(t – t ₀) = 1, t ≥ t ₀.

Функцию включения удобно использовать для аналитического представления различных воздействий, значение которых изменяется скачком в момент коммутации:

s (t)∙1(t – t ₀) = 0, t < t ₀;
s (t)∙1(t – t ₀) = s (t), t ≥ t ₀.

Например, включение источника постоянного напряжения с ЭДС E можно описать следующим образом:

e (t) = E ∙1(t – t ₀).

Другой пример, включение источника гармонического напряжения

e (t) = 1(t – t ₀) E cos(ω t + ψ).

Воздействие в виде прямоугольного импульса может быть представлено как разность двух одинаковых скачков, сдвинутых во времени на длительность импульса Δ t (рис. 1.24):

s (t) = s ₁(t) – s ₂(t) =

= S_m 1(t – t ₀) – S_m 1(t – t ₀ – Δ t) =

= S_m [1(t – t ₀) – 1(t – t ₀ – Δ t)].

Рассмотрим прямоугольный импульс с единичной площадью (рис. 1.25). Устремим длительность импульса к нулю, при этом амплитуда импульса будет стремиться к бесконечности. Предельную функцию, имеющую бесконечно малую длительность, бесконечно большую амплитуду и единичную площадь, называют единичным импульсом, δ- функцией или функцией Дирáка.

Итак,

δ(t) = 0, t ≠ 0;

δ(t) = ∞, t = 0,

причем

.

В общем случае δ-функция может быть смещена относительно начала отсчета времени. Тогда

δ(t – t ₀) = 0, t ≠ t ₀;

δ(t – t ₀) = ∞, t = t ₀.

Временную диаграмму δ-функции условно принято изображать как показано на рис. 1.26.

Установим связь между δ-функцией и функцией включения

Если проинтегрируем обе части равенства, то получим:

,

т. е. δ-функция представляет собой производную функции включения, а функция включения – интеграл от δ-функции.

Найдем спектр δ-функции

= 1,

т. е. спектр δ-функции равномерен во всей полосе частот (рис. 1.27).

Найдем спектр функции включения. Поскольку функция 1(t) не абсолютно интегрируема, то к ней не может быть применено преобразование Фурье. Применим преобразование Фурье к произведению 1(t) e^{‑ α t}, которое абсолютно интегрируемо. Тогда

= .

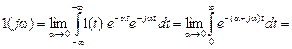
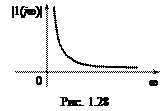Как видно из рис. 1.28, энергия функции включения сосредоточена в основном вблизи нулевой частоты.

Дата добавления: 2017-01-14