Законы электролиза

Мощность в цепи переменного тока.

Мгновенное значение мощности в цепи переменного тока равно произведению мгновенных значений напряжения и силы тока. ,(14.24); где: ,

Используя разложения и 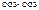, получаем для мгновенного значения мощности: (14.25)

Практический интерес представляет среднее значение мощности за период колебаний. Учитывая, что:

, получаем:

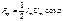.(14.26)

Из векторной диаграммы (рис. 14.4) следует, что 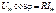. Поэтому: 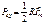. (14.27)

Такую мощность развивает постоянный ток: Величины: (14.28)

называют, соответственно, действующими или эффективными значениями тока и напряжения.

Все вольтметры и амперметры градуируются по действующим значениям тока и напряжения.

Выражения для средней мощности можно записать:

,(14.29); 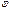- сдвиг фаз между током и напряжением.

1-й закон электролиза: количество вещества , выде-ляющегося на электроде,прямо пропорционально электрич. заряду ,прошедшему через электролит: (16.2). Коэффициен т пропорциональности , численно равный массе в-ва, выделившегося при прохождении через электролит ед-цы электрического заряда, называется электрохимическим эквивалентом вещества. При пропускании через электролит постоянного тока 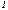в течении с: и .(16.3).

2-й з-н электролиза: электрохимические эквиваленты элементов прямо пропорциональны их химическим эквивалентам: , (16.4); где отношение атомного веса элемента к его валентности называется химическим эквивалентом. Кол-во в-ва, масса которого, выраженная в гр, равна его хим. эквиваленту, называется грамм-эквивалентом. Величина называется числом Фарадея. Число Фарадея 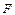равно эл. заряду, который нужно пропустить через электролит, для выделения на электроде 1 грамм-эквивалента любого в-ва: к/г. экв к/г. Экв. Объединенный закон Фарадея формулируется следующим образом: или 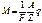, (16.5)т.е. кол-во в-ва, выделяющегося на электроде пропорционально постоянному току 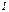, времени протекания , хим. эквиваленту ( - атомный вес элемента, 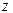- его валентность). Плотность тока в жидкостях 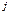равна сумме плотностей токов положительных и отрицательных ионов: 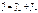.Зависимость плотности тока в жидкостях от напряженности электрического поля имеет вид:

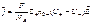, (16.6); 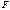- число Фарадея, 1/моль – число Авогадро, - валентность «+» ионов в растворе, 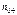- число «+» ионов в ед-це объема электролита, и 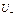подвижности соответственно «+» и «-» ионов, т.е. средние скорости движения этих ионов под действием электрического поля, напряженность которого равна единице. Формула (16.6) выражает закон Ома для плотности тока в электролитах. Удельное сопротивление электролита определяется:

(16.7). Если молекула электролита диссоциируетна 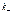положительных и 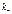отрицательных ионов, то , , ; 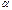- коэффициент диссоциации, 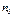- концентрация электролита. В этом случае: или 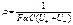(16.8);где - эквивалентная концентрация раствора [кг×экв/м³]. При повышении температуры возрастает подвижность ионов и увеличивается электропроводимость. В биологических мембранах разность потенциалов , образующаяся по разные стороны мембраны получила название мембранного потенциала. Теоретически максимальное значение мембранного потенциала описывается уравнением Нернста: , (16.9); R – газовая постоянная, Т – температура, Z –валентность ионов, F – число Фарадея, с_{1 ,} с₂ - концентрация ионов по обе стороны от мембраны.

Мембранный потенциал зависит от температуры и концентрационного градиента ионов, диффундирующих через мембрану.

60. электрические явления в биологических тканях. Био. ткани и органы яв-ся довольно разнород-ными образованиями с различными эл. сопротивлениями, кот. могут изменяться под действием эл. тока. Электропро-водимость отдельных участков организма, находящихся между электродами, наложенными непосредственно на поверхность тела, существенно зависит от сопротивления кожи и подкожных слоев. Сопротивление кожи, в свою очередь, определяется ее состоянием: толщиной, воз-растом, влажностью. Электропроводимость тканей и орга-нов зависит от их функционального состояния и, следова-тельно, может быть использована как диагностический показатель. Напр, при воспалении, когда клетки набухают, ↓ сечение межкл-ых соединений и ↓ эл. Сопротивление и т.д.

Удельные сопротивления тканей и жидкостей организма:

Ткань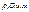
Спинномозговая жидкость	0,55
Кровь	1,66
Мышцы
Ткань мозговая и нервная	14,3
Ткань жировая	33,3
Кожа сухая	10^5
Кость без надкостницы	10^7

Биоэлектрич. явления в организме в большинстве случаев связаны с био-ми мембранами, кот. представляют собой тонкие диэлектрические пленки, разделяющие р-ры элек-тролитов разного состава. В силу того, что мембраны в раз-ной степени проницаемы для катионов и анионов, на них возникает так называемая диффузионная разность потенциалов (рис. 16.1).

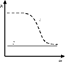
Рис.16.1 Рис.16.3

Напр. из р-ра с высок. Концентрац. (KCl)² идет диффузия катионов в р-р с меньшей концентрацией (KCl)¹, и обратно. В результате справа возникает избыточный «-» заряд, слева – «+». Они создают поле, кот. тормозит переход кати-онов справа – налево и ускоряет их обратный переход. Поле достигает такой величины, когда противоположные потоки уравниваются. Т обр. на мембране устанавливается стационарная разность потенциалов, кот. поддерживается за счет неравновесного распреде-ления концентраций элек-тролитов. Обычно в кл. она составляет примерно 0,1 В. При толщине мембран порядка 10 нм эта разность потенциалов создает очень большую напряженность поля, которая достигает 200 кВ /cм. Такие значения величины напряжен-ности поля оказывают значительное воздействие на пове-дение молекул, встроенных в мембраны. Это приводит к изменению эффективности регуляции многих био-х про-цессов, происходящих в кл.. Тк. организма проводят не только постоянный, но и перемен-ный эл. ток. Био-е мемб-раны и весь организм обладают емкостными свойствами. В связи с этим импеданс тк. орга-низма определяется только омическим и емкостным сопротивлениями. Налич. в био-х системах емкостных эл-о подтверждается тем, что сила тока опережает по фазе приложенное напряжение.

Некоторые значения угла сдвига фаз, полученные при частоте 1 кГц для разных биологических объектов:

Ткань	, град
Кожа человека, лягушки
Нерв лягушки
Мышцы кролика

Омические и емкостные свойства био-х тканей можно моделировать, используя эквивалентные эл. схемы. Наиболее удачна эквивалентная схема: Рис. 16.2. При и сопротивление схемы можно найти как . Частотная зависимость импеданса позволяет оценить жизнеспособность тк. организма, что важно знать для пересадки (трансплантации) тк. и органов. Это можно проиллюстрировать графически (рис.16.3). Кривая 1 нарисована для нормальной здоровой тк., 2 – для мертвой тк. убитой кипячением в воде. В мертвой ткани разрушены мембраны клетки, и тк. обладает лишь омическим сопро-тивлением. Различия в частотных зависимостях импеданса получается и в случаях здоровой и больной тк. О емкостных свойствах тк. также могут давать информацию и зависи-мость узла сдвига фаз между током и напряжением. Импе-данс тканей и органов зависит также и от их физиологич. состояния. Диагностический метод, основанный на регистрации изменения импеданса тк. в процессе сердечной деятельности, называют реографией (импеданс-плетизмографией). Используя указанный метод, получают реограмму головного мозга (реоэнцефалограмма), сердца (реокардиограмма), легких, печени, конечностей. Измерения обычно проводят на частоте 30кГц.

55. Колебательный контур. КОЛЕБАТЕЛЬНЫЙ КОНТУР - электрич. цепь, содержа-щая индуктивность L, ёмкость С и сопротивление R, в к-рой могут возбуждаться электрич. колебания (рис. 1).К. к.- электрич. осциллятор, один из осн. элементов радиотехн. систем. Различают линейные и нелинейные К. к. В линей-ном К. к. его параметры L, С и Я не зависят от интенсивно-сти колебаний и период колебаний не зависит от ампли-туды (изохронность колебаний). При отсутствии потерь (R =0) в линейном К. к. происходят свободныегармонические колебания с частотой: w₀ = 1/ (ф-ла Томп-сона). Электрич. энергия колебаний сосредоточивается в ёмкости: W_э = a²/2C,а магн.-в катушк индуктивн.ости: W_м =L q’²/2. Периодически с периодом π/w происходит преобразова-ние эл. энергии в магн. а затем обратно так что полная энергия системы W (t) =W _э (t)+W_м (t)=const = W _э (t₀); где t₀ - нач.момент зарядки конденсатора, q - заряд на кон-денсаторе. В реальных К. к. из-за наличия потерь при 0<R<2ρ (где ρ= 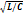устанавливаются затухающие колебания с час-тотой: w = и амплитудой, пропорцииональной e^-δt, где δ = R/2L - затухание контура. Качество К. к. хар-ся его добротностью Q = ρ/R = w₀/2δ. При R > 2ρ в К. к. колебания отсутствуют и происходит апериодич. Процесс разряда конденсатора через катушку индуктивности. При включении в линейный К. к. генератора с переменной эдс: E = E₀ cos Ωt в нём устанавливают-ся вынужденные колебания с частотой Ω. Напр., при последоват. включении эдс амплитуда колебаний напряжения V на конденсаторе, определяемая соотношением: 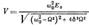зависит не толь-ко от амплитуды внеш. эдс, но и от её частоты Ω. Зависи-мость амплитуды колебаний в К. к. от Ω наз. резонансной характеристикой контура (рис. 2). При Ω = w₀ V при-нимает макс. значение, в Q раз превышающее амплитуду внеш. силы Е₀. Величину ∆Ω = w/Q наз. полосой пропу-скания К. к. На резонансной характеристике - это область частот вблизи w₀, соответствующая значению амплитуды V ≈ 0,7QE₀. Резонансные свойства К. к. позволяют выделить из множества колебаний те, частоты которых близки к w₀. Именно это свойство (избирательность) К. к. используется на практике. Линейный К. к. описывается дифференц. ур-ем вида: q’’ + 2Cq’ + w₀²q = E₀ cos Ωt т. е. является (при Е₀=0)системой с одной степенью свобо-ды. Незатухающим колебаниям в К. к. без потерь (δ=0, Е₀ =0) на фазовой плоскости соответ-ствуют замкнутые интегральные кривые линейного центра (рис. 3) - вложенные друг в друга эллипсы или, в частном случае, окружности. В нелинейном К. к., когда за-ряд на конденсаторе g - нелинейная ф-ция напряжения или индук-тивность катушки L - нелинейная ф-ция тока (напр., в слу-чае конденсатора с сегнетоэлектриком и индуктивности с ферромагн. сердечником), колебания будут негармоничес-кими и незатухающим колебаниям на фазовой плоскости соответствуют замкнутые интегральные кривые, период обращения по к-рым зависит от энергии, запасённой в К. к.; при этом частота колебаний становится зависимой от амп-литуды колебаний. С помощью К. к. часто моделируют бо-лее сложн. физ. системы, напр. резонаторы с одной эфф. степенью свободы.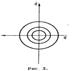

61. Физические основы электрокардиографии. Живые тк. явл-тся источником эл. потенциалов (биопотенциалов). Регистрация биопотенциалов органов и тканей с диагности-ческой целью получила название электрографии. В практике распространены названия соответствующих диагностических методов: электрокардиография (ЭКГ)- регистрация биопотенциалов, возникающих в сердечной мышце, при ее возбуждении, электромиография - метод регистрации биологической активности мышц; электроэнцефалография (ЭЭГ)- метод регистрации биологической активности мозга. В большинстве случаев биопотенциалы снимаются электродами не непосредственно с органа, а с других тканей, в которых электрические поля этим органом создаются. В клиническом отношении это упрощает процедуру регистрации, делая ее безопасной. Физический подход к выяснению связи между биопотенциалами сердца и их адекватной регистрацией заключается в моделировании источников этих потенциалов. Все сердце в электрическом отношении представляется как некоторый эквивалентный электрический генератор (рис.16.4). Для потенциала в некоторой точке можно записать (выражение для потенциала электрического поля вне системы зарядов, распространенных в некотором пространстве): 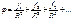(16.9); - расстояние от системы зарядов до т. А с потенциалом ; 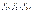.-некоторые функции, зависящие от мультиполя, его зарядов и направления на т. А. При больших значения , можно ограничиться дипольным приближением и получить: (16.10); - дипольный момент дипольного электрического генератора. В мультипольном эквивалентном генераторе сердца основной вклад в потенциал на поверхности тела человека вносится его дипольной составляющей. Дипольное представление лежит в основе теории отведения Эйтховена. Согласно ей, сердце представляет собой диполь с дипольным моментом 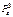, который поворачивается, изменяя свое положение и точку приложения (изменением положения этого вектора часто пренебрегают) за время сердечного цикла. На рис.16.4 показаны положения вектора и эквипотенциальных линий для момента времени, когда дипольный момент максимален; это соответствует зубцу на электрокардиограмме. В табл.3 приведены значения максимального дипольного момента для человека и некоторых животных, они сопоставляются с массами сердца и тела. В. Эйтховен предложил снимать разность

Объект	Масса сердце	Масса тела	Макс. Дипольн. момент сердца
Лягушка	0,16г	0,036кг	0,005 мА×см
Крыса	1,10г	0,287кг	0,107 мА×см
Собака	108г	14,2кг	0,163 мА×см
Человек	300г	71,5кг	2,32 мА×см
Лошадь	3060г	419кг	13,0 мА×см

биопотенциалов между вершинами равностороннего треугольника, которые приближенно расположены в правой ПР и левой ЛР руке и левой ноге ЛН (рис.16. 4).

Эл.Оси сердца. На рис схематически изображен этот треугольник. Разность потенциалов, регистрируемых между двумя точками тела, называют отведением. Различает I отведение (правая рука - левая рука), II отведение (правая рука - левая нога) и III отведение (левая рука - левая нога), соответствующие разностям потенциалов: . По Эйнтховену, сердце расположено в центре треугольника. Отведения позволяют определить потенциалы согласно выражению: ,где соотношение значений разности потенциалов определяется отношением проекций электрического момента сердца на стороны треугольника. Т.к. электрический момент диполя- сердца – изменяется со временем, то в отведениях будут получены временные зависимости напряжения, которые и называются электрокардиограммами. ЭКГ не дает представления о пространственной ориентации вектора . Однако для диагностических целей такая информация важна. В связи с этим иногда применяют метод пространственного исследования электрического поля сердца, называемый вектор - кардиограммой. Вектор кардиограмма - геометрическое место точек, соответствующих концу вектора 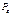, положение которого изменяется за время сердечного цикла.

Дата добавления: 2017-01-14