Производная сложной функции. Примеры решений

Фундаментальные отрасли психологии разрабатывают общие проблемы и изучают общие закономерности психики, проявляющиеся у людей вне зависимости оттого, какой деятельностью они занимаются. В силу универсальности знания фундаментальных отраслей психологии объединяют термином«общая психология».

Структура психологии как наука.

Психология на современном уровне развития представляет собой весьма разветвленную систему научных дисциплин, подразделяющихся на фундаментальные и прикладные.

Общая психология исследует индивида, выделяя в нем психические познавательные процессы и личность. Психология познавательных процессов изучает такие психические процессы, как ощущения, восприятие, внимание, память, воображение, мышление, речь. В психологии личности исследуется психическая структура личности и психические свойства личности, определяющие дела и поступки человека.

Помимо общей психологии, психологическая наука включает в себя целый ряд специальных психологических дисциплин, находящихся на разных ступенях формирования, связанных с различными областями человеческой жизни и деятельности.

Среди специальных отраслей психологии, изучающих психологические проблемы конкретных видов деятельности, выделяют: психологию труда, педагогическую психологию, медицинскую психологию, юридическую психологию, военную психологию, психологию торговли, психологию научного творчества, психологию спорта и т.д.

Психологические аспекты развития изучают возрастная психология и психология аномального развития.

Психологические аспекты отношений личности и общества исследует социальная психология.

Теория и практика обучения и воспитания подрастающего поколения тесно связана как с обшей психологией, так и со специальными отраслями психологии.

Научной основой для понимания законов психического развития ребенка являются генетическая, дифференциальная и возрастная психология. Генетическая психология изучает наследственные механизмы психики и поведения ребенка. Дифференциальная психология выявляет индивидуальные различия между людьми и объясняет процесс их формирования. В возрастной психологии исследуются этапы психического развития индивидуума.

Для психически грамотной организации воспитания нужно знать психологические закономерности взаимодействия людей в группах, таких, как семья, ученический и студенческий коллективы. Взаимоотношения в группах являются предметом изучения социальной психики.

Психология аномального развития имеет дело с отклонениями от нормы в поведении и психике человека и крайне необходима при педагогической работе с детьми, отстающими в психическом развитии.

Педагогическая психология объединяет всю информацию, связанную с обучением и воспитанием. Предмет педагогической психологии — психологические закономерности обучения и воспитания человека. Разделами педагогической психологии являются:

§ психология обучения (психологические основы дидактики, частных методик, формирования умственных действий);

§ психология воспитания (психологические основы воспитания, психологические основы исправительно-трудовой педагогики);

§ психология учебно-воспитательной работы с трудными детьми;

§ психология учителя.

Для современной психологии характерен как процесс дифференциации, порождающий многочисленные специальные отрасли психологии, так и процесс интеграции, в результате которого происходит стыковка психологии с другими науками, например, через педагогическую психологию с педагогикой.

Пример 1

Найти производную функции

Под синусом у нас находится не просто буква «икс», а целое выражение 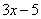, поэтому найти производную сразу по таблице не получится. Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя:

В данном примере уже из моих объяснений интуитивно понятно, что функция – это сложная функция, причем многочлен 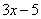является внутренней функцией (вложением), а – внешней функцией.

Первый шаг, который нужно выполнить при нахождении производной сложной функции состоит в том, чтобы разобраться, какая функция является внутренней, а какая – внешней.

В случае простых примеров вроде понятно, что под синус вложен многочлен 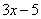. А как же быть, если всё не очевидно? Как точно определить, какая функция является внешней, а какая внутренней? Для этого я предлагаю использовать следующий прием, который можно проводить мысленно или на черновике.

Представим, что нам нужно вычислить на калькуляторе значение выражения при (вместо единицы может быть любое число).

Что мы вычислим в первую очередь? В первую очередь нужно будет выполнить следующее действие: , поэтому многочлен 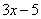и будет внутренней функцией :

Во вторую очередь нужно будет найти , поэтому синус – будет внешней функцией:

После того, как мы РАЗОБРАЛИСЬ с внутренней и внешней функциями самое время применить правило дифференцирования сложной функции .

Начинаем решать. Из урока Как найти производную? мы помним, что оформление решения любой производной всегда начинается так – заключаем выражение в скобки и ставим справа вверху штрих:

Сначала находим производную внешней функции (синуса), смотрим на таблицу производных элементарных функций и замечаем, что 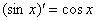. Все табличные формулы применимы и в том, случае, если «икс» заменить сложным выражением, в данном случае:

Обратите внимание, что внутренняя функция не изменилась, её мы не трогаем.

Ну и совершенно очевидно, что

Результат применения формулы в чистовом оформлении выглядит так:

Далее мы берем производную внутренней функции, она очень простая:

Постоянный множитель обычно выносят в начало выражения:

Готово

Если осталось какое-либо недопонимание, перепишите решение на бумагу и еще раз прочитайте объяснения.

Пример 2

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

Пример 3

Найти производную функции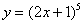

Как всегда записываем:

Разбираемся, где у нас внешняя функция, а где внутренняя. Для этого пробуем (мысленно или на черновике) вычислить значение выражения 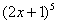при . Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание: , значит, многочлен – и есть внутренняя функция:

И, только потом выполняется возведение в степень , следовательно, степенная функция – это внешняя функция:

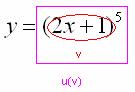
Согласно формуле , сначала нужно найти производную от внешней функции, в данном случае, от степени. Разыскиваем в таблице нужную формулу: . Повторяем еще раз: любая табличная формула справедлива не только для «икс», но и для сложного выражения. Таким образом, результат применения правила дифференцирования сложной функции следующий:

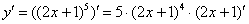
Снова подчеркиваю, что когда мы берем производную от внешней функции , внутренняя функция у нас не меняется:

Теперь осталось найти совсем простую производную от внутренней функции и немного «причесать» результат:

Готово.

Пример 4

Найти производную функции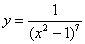

Это пример для самостоятельного решения (ответ в конце урока).

Для закрепления понимания производной сложной функции приведу пример без комментариев, попробуйте самостоятельно разобраться, порассуждать, где внешняя и где внутренняя функция, почему задания решены именно так?

Пример 5

а) Найти производную функции

б) Найти производную функции

Пример 6

Найти производную функции

Здесь у нас корень, а для того, чтобы продифференцировать корень, его нужно представить в виде степени . Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид:

Анализируя функцию, приходим к выводу, что сумма трех слагаемых – это внутренняя функция, а возведение в степень – внешняя функция. Применяем правило дифференцирования сложной функции :

Степень снова представляем в виде радикала (корня), а для производной внутренней функции применяем простое правило дифференцирования суммы:

Готово. Можно еще в скобках привести выражение к общему знаменателю и записать всё одной дробью. Красиво, конечно, но когда получаются громоздкие длинные производные – лучше этого не делать (легко запутаться, допустить ненужную ошибку, да и преподавателю будет неудобно проверять).

Пример 7

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

Интересно отметить, что иногда вместо правила дифференцирования сложной функции можно использовать правило дифференцирования частного 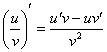, но такое решение будет необычно. Вот характерный пример:

Пример 8

Найти производную функции

Здесь можно использовать правило дифференцирования частного 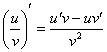, но гораздо выгоднее найти производную через правило дифференцирования сложной функции:

Подготавливаем функцию для дифференцирования – выносим минус за знак производной, а косинус поднимаем в числитель:

Косинус – внутренняя функция, возведение в степень – внешняя функция.
Используем наше правило :

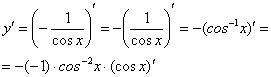
Находим производную внутренней функции, косинус сбрасываем обратно вниз:

Готово. В рассмотренном примере важно не запутаться в знаках. Кстати, попробуйте решить его с помощью правила 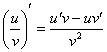, ответы должны совпасть.

До сих пор мы рассматривали случаи, когда у нас в сложной функции было только одно вложение. В практических же заданиях часто можно встретить производные, где, как матрешки, одна в другую, вложены сразу 3, а то и 4-5 функций.

Пример 9

Найти производную функции

Разбираемся во вложениях этой функции. Пробуем вычислить выражение с помощью подопытного значения . Как бы мы считали на калькуляторе?

Сначала нужно найти , значит, арксинус – самое глубокое вложение:

Затем этот арксинус единицы следует возвести в квадрат :

И, наконец, семерку возводим в степень :

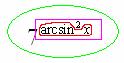
То есть, в данном примере у нас три разные функции и два вложения, при этом, самой внутренней функцией является арксинус, а самой внешней функцией – показательная функция.

Начинаем решать

Согласно правилу сначала нужно взять производную от внешней функции. Смотрим в таблицу производных и находим производную показательной функции: 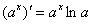Единственное отличие – вместо «икс» у нас сложное выражение , что не отменяет справедливость данной формулы. Итак, результат применения правила дифференцирования сложной функции следующий:

Под штрихом у нас снова сложная функция! Но она уже проще. Легко убедиться, что внутренняя функция – арксинус, внешняя функция – степень. Согласно правилу дифференцирования сложной функции сначала нужно взять производную от степени:

Теперь все просто, находим по таблице производную арксинуса и немного «причесываем» выражение:

Готово.

Пример 10

Найти производную функции

Сначала используем правило дифференцирования суммы , заодно в первом слагаемом выносим постоянный множитель за знак производной по правилу :

В обоих слагаемых под штрихами у нас находится произведение функций, следовательно, нужно дважды применить правило :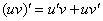

Замечаем, что под некоторыми штрихами у нас находятся сложные функции , 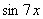. Каламбур, но это простейшие из сложных функций, и при определенном опыте решения производных Вы будете легко находить их устно.
А пока запишем подробно, согласно правилу , получаем:

Дата добавления: 2017-01-14