Теплопроводность

ТЕПЛООБМЕННЫЕ ПРОЦЕССЫ

Контрольные задания к разделу

6.1 Манометр парового котла показывает давление P, бар. Показания барометра 776 мм.рт.ст.

Считая пар сухим насыщенным, определить его температуру, удельный объём и энтальпию.

6.2 Найти давление, удельный объём и плотность воды, если она находится в состоянии кипения и температура её равна t.

6.3 Определить влагосодержание воздуха при температуре t°С ибарометрическом давлении P_бар = 735 мм. рт. ст, если относительнаявлажность воздуха φ = 60 %.

6.4 Состояние влажного воздуха характеризуется температурой t = 25°С и относительной влажностью φ %. Барометрическое давление, при котором находится воздух, равно 745 мм рт. ст. Найти парциальное давление пара в воздухе и его влагосодержание. Найти на диаграмме i,d точку, соответствующую состоянию воздуха, определить издиаграммы d и сравнить с результатом решения.

Задача	Значение	№ варианта
6.1	Р, бар	1,5		2,5		3,5		4,5		5,5
6.2	t, °С
6.3	t, °С
6.4	φ, %

Различают три вида теплообмена: теплопроводность (или кондукция), конвекция и тепловое излучение.

Теплопроводностью называется перенос теплоты, возникающий при непосредственном соприкосновении между частицами тела.

В жидкостях наряду с теплопроводностью теплота может распространяться также путем перемещения и перемешивания между собой более или менее нагретых частиц самой жидкости. Такой вид распространения теплоты называется конвекцией. В целом явление передачи теплоты при соприкосновении стенки с жидкостью путем теп­лопроводности и дальнейшее распространение ее в жидкости за счет конвекции (а также процесс, протекающий в обратном направлении) называется конвективным теплообменом или теплоотдачей.

Тепловым излучением или лучеиспусканием, называется и перенос энергии в виде электромагнитных волн между двумя взаимно излучающими поверхностями. При этом происходит двойное прев­ращение энергии: тепловой энергии в лучистую на поверхности тела, излучающего теплоту, и лучистой энергии в тепловую на поверхности тела, поглощающего лучистую теплоту.

Температура, как известно, характеризует тепловое состояние тела и определяет степень его нагретости. Так как тепловое состояние отдельных частей тела в процессе теплопроводности различно, то в общем случае температура t является функцией координат х, у, z и времени τ, т. е.:

t=f(x,y,z,τ). (3.1)

Совокупность значений температуры для всех точек пространства в данный момент времени называется температурным полем. Уравнение (3.1) является математической формулировкой такого поля.

При любом температурном поле в теле всегда имеются точки с одинаковой температурой. Геометрическое место таких точек образует изотермическую поверхность.

Предел отношения изменения температуры Δt к расстоянию между изотермами по нормали n (см. рис. 3.1) называется градиентом температур и обозначается одним из следующих символов:

(3.2)

Температурный градиент является вектором, направленным по нормали к изотермической поверхности в сторону возрастания температуры, его размерность °С/м.

Рис. 3.1. К определению Рис. 3.2. Закон Фурье

температурного градиента

Тепло самопроизвольно переносится только в сторону убывания температуры. Количество тепла, переносимого через какую-либо поверхность в единицу времени, называется тепловым потоком Q (Вт). Тепловой поток, отнесённый к единице поверхности, называется плотностью теплового потока, или удельным тепловым потоком, или тепловой нагрузкой поверхности q (Вт/м²). Если тепловой поток отнесен к единице изотермической поверхности, то величина q является вектором, направление которого совпадает с направлением распространения тепла в данной точке и противоположно направлению вектора температурного градиента (рис. 3.2).

Изучая процесс теплопроводности в твердых телах, экспериментально установлено, что количество переданного тепла пропорционально падению температуры, времени и площади сечения, перпендикулярного направлению распространения тепла. Данное выражение именуется законом Фурье. Если количество переданного тепла отнести к единице сечения и единице времени, то установленную зависимость можно записать:

(3.3)

Величина λ в уравнении (3.3) есть коэффициент теплопроводности. Это физический параметр вещества, характеризующий его способность проводить теплоту. Его размерность Вт/(м ^. К). Коэффициент теплопроводности численно равен количеству теплоты, проходящей через единицу изотермной поверхности в единицу времени, при условии, что градиент температуры равен единице. Коэффициент теплопроводности жидкостей и газов зависит от давления и температуры, а твёрдых тел – так же и от плотности, влажности и пористости материала.

Рассмотрим однородную стенку толщиной (рис. 3.3), кoэффициeнт теплопроводности которой постоянен и равен λ. На наружных поверхностях стенки поддерживаются постоянные температуры t₁ и t₂. Температура изменяется только в направлении оси х. В этом случае температурное поле одномерно, изотермические поверхности плоские и располагаются перпендикулярно оси х.

Рис. 3.3. Однородная Рис. 3.4. Многослойная

плоская стенка плоская стенка

Согласно закону Фурье удельный тепловой поток, проходящий через однослойную стенку определяется по формуле:

(3.4)

Отношение λ/δ называется тепловой проводимостью стенки, а обратная величина δ/λ её тепловым или термическим сопротивлением. Последнее определяет падение температуры при прохождении через стенку теплового потока равного единице.

Стенки, состоящие из нескольких разнородных слоёв, называются многослойными (см. рис. 3.4). Именно такими являются, например стены жилых домов, в которых на основном кирпичном слое с одной стороны имеется внутренняя штукатурка, с другой – внешняя облицовка.

При стационарном режиме удельный тепловой поток q постоянен и для всех слоев одинаков. Поэтому на основании (3.4) можно написать:

. (3.5)

Решением системы уравнений является значение удельного теплового потока:

(3.6)

По аналогии с изложенным можно сразу написать расчётную формулу для n -слойной стенки:

(3.7)

Так как каждое слагаемое знаменателя в (3.6) представляет собой термическое сопротивление слоя, то из уравнения следует, что общее термическое сопротивление многослойной стенки равно сумме частных сопротивлений [уравнение (3.7)].

Значения неизвестных температур t₂ и t₃ многослойной стенки можно определить также графически (рис.3.5) При построении графика по оси абсцисс в любом масштабе, но в порядке расположения слоев откладываются значения их термических сопротивлений δ₁/λ₁, δ₂/λ₂ и δ₃/λ₃ и восстанавливаются перпендикуляры. На крайних из них также в произвольном, но одинаковом масштабе откладываются значения наружных температур t₁ и t₄. Полученные точки А и С соединяются прямой. Точки пересечения этой прямой со средними перпендикулярами дают значения искомых температур t₂ и t₃. При таком построении Δ АВС ~ ΔADE. Следовательно,

и

Подставляя значения отрезков, получаем:

Аналогичным образом доказывается, что:

MN = q (δ₁ /λ₁ + δ₂ /λ₂) = t₁-t₃.

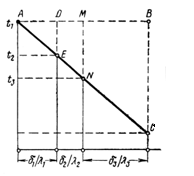
Рис. 3.5. Графический способ определения промежуточных температур

Рассмотрим однородную цилиндрическую стенку (трубу) длиной l, м, с внутренним радиусом r₁ и внешним r₂. Коэффициент теплопроводности материала постоянен и равен λ. Внутренняя и внешняя поверхности поддерживаются при постоянных температурах t₁ и t₂, причем t₁>t₂ (рис.3.6), и температура изменяется только в радиальном направлении r.

Согласно закону Фурье количество тепла, проходящего в единицу времени через этот слой, равно:

(3.8)

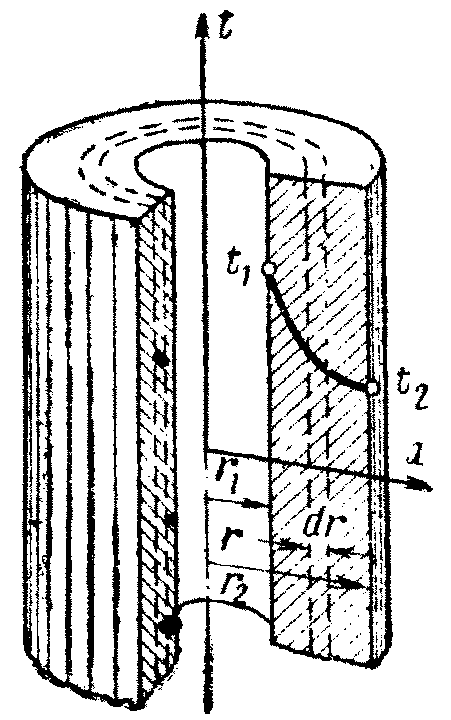
Рис. 3.6. Однородная цилиндрическая стенка

Преобразовав последнее уравнение, подставим значения переменных на границах стенки (при r = r₁, t= t₁ и при r = r₂t= t₂) и исключив постоянную интегрирования, получаем следующую расчетную формулу:

(3.9)

Количество тепла, проходящее через стенку трубы, может быть отнесено либо к единице длины l, либо к единице внутренней F₁ или внешней F₂ поверхности трубы. При этом расчетные формулы соответственно принимают следующий вид:

(3.10)

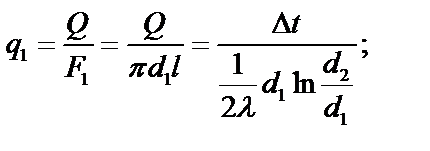(3.11)

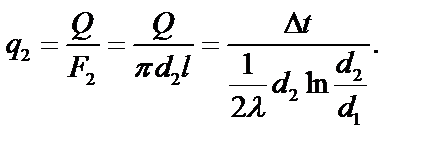(3.12)

Величина q_l, Вт/м², называется линейной плотностью теплового потока.

Уравнение температурной кривой внутри однородной цилиндрической стенки выводится из уравнения (3.15) Подставляя сюда значения Q и С, имеем:

(3.13)

Следовательно, в этом случае при постоянном значении λ температура изменяется по логарифмической кривой (см. рис.3.6).

Пусть цилиндрическая стенка состоит из трех разнородных слоев. Диаметры и коэффициенты теплопроводности отдельных слоев известны, их обозначения см. на рис.3.7. Кроме того,известны температуры внутренней и внешней поверхностей многослойной стенки t₁ и t₄.

Рис. 3.7. Многослойная цилиндрическая стенка

В местах же соприкосновения слоев температуры неизвестны, обозначим их через t₂ и t₃. При стационарном тепловом режиме через все слои проходит одно и то же количество тепла. Поэтому на основании (3.10) можно написать:

(3.14)

По аналогии с однослойной цилиндрической стенокй можно написать расчетную формулу для n -слойной стенки:

(3.15)

Дата добавления: 2017-01-14