
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Средние показатели ряда динамики
|
|
|
|
Виды рядов динамики
Ряды динамики
Понятие рядов динамики (временных рядов)
Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, то есть их динамика. Эта задача решается при помощи анализа рядов динамики (временных рядов).
Ряд динамики (или временной ряд) – это числовые значения определенного статистического показателя в последовательные моменты или периоды времени (т.е. расположенные в хронологическом порядке).
Числовые значения того или иного статистического показателя, составляющего ряд динамики, называют уровнями ряда и обычно обозначают буквой y. Первый член ряда y1 называют начальным или базисным уровнем, а последний yn – конечным. Моменты или периоды времени, к которым относятся уровни, обозначают через t.
Ряды динамики, как правило, представляют в виде таблицы или графика, причем по оси абсцисс строится шкала времени t, а по оси ординат – шкала уровней ряда y.
Ряды динамики классифицируются по следующим основным признакам:
1. По времени — ряды моментные и интервальные (периодные), которые показывают уровень явления на конкретный момент времени или на определенный его период. Сумма уровней интервального ряда дает вполне реальную статистическую величину за несколько периодов времени, например, общий выпуск продукции, общее количество проданных акций и т.п. Уровни моментного ряда, хотя и можно суммировать, но эта сумма реального содержания, как правило, не имеет. Так, если сложить величины запасов на начало каждого месяца квартала, то полученная сумма не означает квартальную величину запасов.
2. По форме представления — ряды абсолютных, относительных и средних величин.
3. По интервалам времени — ряды равномерные и неравномерные (полные и неполные), первые из которых имеют равные интервалы, а у вторых равенство интервалов не соблюдается.
4. По числу смысловых статистических величин — ряды изолированные и комплексные (одномерные и многомерные). Первые представляют собой ряд динамики одной статистической величины (например, индекс инфляции), а вторые — нескольких (например, потребление основных продуктов питания).
Каждый ряд динамики можно рассматривать как некую совокупность n меняющихся во времени показателей, которые можно обобщать в виде средних величин. Такие обобщенные (средние) показатели особенно необходимы при сравнении изменений того или иного показателя в разные периоды, в разных странах и т.д.
Обобщенной характеристикой ряда динамики может служить прежде всего средний уровень ряда. Способ расчета среднего уровня зависит от того, моментный ряд или интервальный (периодный).
В случае интервального ряда его средний уровень определяется по формуле простой средней арифметической величины из уровней ряда, т.е.
 =
= 
Если имеется моментный ряд, содержащий n уровней (y1, y2, …, yn) с равными промежутками между датами (моментами времени), то такой ряд легко преобразовать в ряд средних величин. При этом показатель (уровень) на начало каждого периода одновременно является показателем на конец предыдущего периода. Тогда средняя величина показателя для каждого периода (промежутка между датами) может быть рассчитана как полусуммазначений у на начало и конец периода, т.е. как  . Количество таких средних будет
. Количество таких средних будет 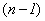 . Как указывалось ранее, для рядов средних величин средний уровень рассчитывается по средней арифметической. Следовательно, можно записать
. Как указывалось ранее, для рядов средних величин средний уровень рассчитывается по средней арифметической. Следовательно, можно записать
 .
.
После преобразования числителя получаем
 ,
,
где Y1 и Yn — первый и последний уровни ряда; Yi — промежуточные уровни.
Эта средняя  известна в статистике как средняя хронологическая для моментных рядов. Такое название она получила от слова «cronos» (время, лат.), так как рассчитывается из меняющихся во времени показателей.
известна в статистике как средняя хронологическая для моментных рядов. Такое название она получила от слова «cronos» (время, лат.), так как рассчитывается из меняющихся во времени показателей.
В случае неравных промежутков между датами среднюю хронологическую для моментного ряда можно рассчитать как среднюю арифметическую из средних значений уровней на каждую пару моментов, взвешенных по величине расстояний (отрезков времени) между датами, т.е.

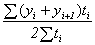 .
.
В данном случае предполагается, что в промежутках между датами уровни принимали разные значения, и мы из двух известных (yi и yi+1) определяем средние, из которых затем уже рассчитываем общую среднюю для всего анализируемого периода.
Если же предполагается, что каждое значение yi остается неизменным до следующего (i+ 1 )- го момента, т.е. известна точная дата изменения уровней, то расчет можно осуществлять по формуле средней арифметической взвешенной:
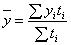 ,
,
где  – время, в течение которого уровень
– время, в течение которого уровень  оставался неизменным.
оставался неизменным.
Кроме среднего уровня в рядах динамики рассчитываются и другие средние показатели – среднее изменение уровней ряда (базисным и цепным способами), средний темп изменения.
Базисное среднее абсолютное изменение представляет собой частное от деления последнего базисного абсолютного изменения на количество изменений. То есть
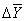 Б =
Б = 
Цепное среднее абсолютное изменение уровней ряда представляет собой частное от деления суммы всех цепных абсолютных изменений на количество изменений, то есть
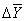 Ц =
Ц = 
По знаку средних абсолютных изменений также судят о характере изменения явления в среднем: рост, спад или стабильность.
Из правила контроля базисных и цепных абсолютных изменений следует, что базисное и цепное среднее изменение должны быть равными.
Наряду со средними абсолютным изменением рассчитывается и среднее относительное тоже базисным и цепным способами.
Базисное среднее относительное изменение определяется по формуле
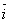 Б=
Б=  =
= 
Цепное среднее относительное изменение определяется по формуле
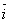 Ц=
Ц= 
Естественно, базисное и цепное среднее относительное изменения должны быть одинаковыми и сравнением их с критериальным значением 1 делается вывод о характере изменения явления в среднем: рост, спад или стабильность.
Вычитанием 1 из базисного или цепного среднего относительного изменения образуется соответствующий средний темп изменения, по знаку которого также можно судить о характере изменения изучаемого явления, отраженного данным рядом динамики.
Средний уровень динамического ряда. Способы его исчисления.
Средний уровень ряда в статистике Средний уровень ряда определяет обобщенную величину абсолютных уровней. Он определяется по средней, исчисленной из значений, меняющихся во времени. Методы расчета среднего уровня интервального и моментного рядов динамики разные. Средний уровень из абсолютных уровней для интервальных рядов динамики рассчитывается по формуле средней арифметической: 1. При равных интервалах используют среднюю арифметическую простую: где у — абсолютные уровни ряда; n — число уровней ряда. 2. При неравных интервалах используют среднюю арифметическую взвешенную: где у1,...,уn — уровни ряда динамики; t1,... tn — веса, длительность интервалов времени. Средний уровень моментного ряда динамики рассчитывается по формуле: 1. С равностоящими уровнями рассчитывается по формуле средней хронологической моментного ряда: где у1,...,уn — уровни периода, за который делается расчет; n — число уровней; n-1 — длительность периода времени. 2. С неравностоящими уровнями рассчитывается по формуле средней хронологической взвешенной: где у1,...,уn — уровни рядов динамики; t — интервал времени между смежными уровнями
Одним из важнейших направлений анализа рядов динамики является изучение особенностей развития явления за отдельные периоды времени. С этой целью для динамических рядов рассчитывают ряд показателей:
1. Абсолютный прирост - разность между двумя уровнями ряда динамики, имеет ту же размерность, что и уровни самого ряда динамики. Абсолютные приросты могут быть цепными и базисными, в зависимости от способа выбора базы для сравнения:
2. цепной абсолютный прирост -  ;
3. базисный абсолютный прирост - ;
3. базисный абсолютный прирост -  - средний абсолютный прирост может быть получен по одной из формул:
- средний абсолютный прирост может быть получен по одной из формул:  или или  , где n - число уровней ряда динамики; , где n - число уровней ряда динамики;  - первый уровень ряда динамики; - первый уровень ряда динамики;  - последний уровень ряда динамики; - последний уровень ряда динамики;  - цепные абсолютные приросты..
1. Темп роста - относительный показатель, получающийся в результате деления двух уровней одного ряда друг на друга. Темпы роста могут рассчитываться как:
2. цепные, когда каждый уровень ряда сопоставляется с предшествующим ему уровнем: - цепные абсолютные приросты..
1. Темп роста - относительный показатель, получающийся в результате деления двух уровней одного ряда друг на друга. Темпы роста могут рассчитываться как:
2. цепные, когда каждый уровень ряда сопоставляется с предшествующим ему уровнем:  ;
3. базисные, когда все уровни ряда сопоставляются с одним и тем же уровнем ;
3. базисные, когда все уровни ряда сопоставляются с одним и тем же уровнем  , выбранным за базу сравнения: , выбранным за базу сравнения:  .
4. средний темп роста можно определить, пользуясь формулами: .
4. средний темп роста можно определить, пользуясь формулами:
 или или  где n - число рассчитанных цепных или базисных темпов роста;
где n - число рассчитанных цепных или базисных темпов роста;  - уровень ряда, принятый за базу для сравнения; - уровень ряда, принятый за базу для сравнения;  - последний уровень ряда; Т - цепные темпы роста (в коэффициентах); Темпы роста могут быть представлены в виде коэффициентов либо в виде процентов.
Темп прироста - относительный показатель, показывающий на сколько процентов один уровень ряда динамики больше (или меньше) другого, принимаемого за базу для сравнения.
Базисные темпы прироста: - последний уровень ряда; Т - цепные темпы роста (в коэффициентах); Темпы роста могут быть представлены в виде коэффициентов либо в виде процентов.
Темп прироста - относительный показатель, показывающий на сколько процентов один уровень ряда динамики больше (или меньше) другого, принимаемого за базу для сравнения.
Базисные темпы прироста:   . Цепные темпы прироста: . Цепные темпы прироста: 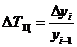 . Существует связь между темпами роста и прироста: . Существует связь между темпами роста и прироста:  Т = Т - 1 или Т = Т - 1 или  Т = Т - 100 % (если темпы роста определены в процентах). Средний темп прироста определяется Т = Т - 100 % (если темпы роста определены в процентах). Средний темп прироста определяется  Т = Т - 100 %
Абсолютное значение одного процента прироста получается путем деления абсолютного прироста (цепного) на темп прироста (цепной) за соответствующий период Т = Т - 100 %
Абсолютное значение одного процента прироста получается путем деления абсолютного прироста (цепного) на темп прироста (цепной) за соответствующий период
 Средний уровень ряда динамики
В зависимости от типа ряда динамики используются различные расчетные формулы:
§ для интервального ряда абсолютных величин с равными периодами (интервалами времени):
Средний уровень ряда динамики
В зависимости от типа ряда динамики используются различные расчетные формулы:
§ для интервального ряда абсолютных величин с равными периодами (интервалами времени):
 ;
§ Моментный ряд с равными интервалами между датами: ;
§ Моментный ряд с равными интервалами между датами:
 - Моментный ряд с неравными интервалами между датами: - Моментный ряд с неравными интервалами между датами:  где где  - уровни ряда, сохраняющиеся без изменения на протяжении интервала времени - уровни ряда, сохраняющиеся без изменения на протяжении интервала времени  . .
|
Задача №25
Произведите группировку хозяйств по площади сельскохозяйственных угодий. Образуйте три группы со следующими интервалами: до 3000; 3000 - 4500; свыше 4500. По каждой группе и по всем хозяйствам вместе подсчитайте:
а) число хозяйств по группам;
б) площадь сельскохозяйственных угодий, га;
в) поголовье коров, гол;
г) поголовье коров на 100 га сельскохозяйственных угодий, гол.
Решение задачи оформите статистической таблицей.
Решение:
1. Выбор группировочного признака – площадь с/х угодий
2. Число групп п=3
3. Интервалы не равные до 3000, 3000-4500, свыше 4500
4. Пропускаем т.к. интервалы даны
5. Составим группировочную таблицу
| №группы | Интервал | Перечень хозяйств | Площадь сх угодий (га) | Поголовье коров (гол.) | Поголовье коров на 100 га (гол.) |
| До 3000 | |||||
| Итого по группе: | |||||
| 3000-4500 | |||||
| Итого по группе: | |||||
| Свыше 4500 | |||||
| Итого по группе: | |||||
| Всего по совокупности: |
6. Подсчитаем итог по каждой группе и в целом по совокупности
7.Анализ полученных результатов:
Наибольшее число хозяйств находится во 2 группе- 10.
Поголовье коров на 100 га – 304 головы, колличество коров – 12356 голов.
Задача 36.
| № группы | Группа коров по среднегодовому надою молока,кг | Число коров в группе,гол |
| 2100-2500 | ||
| 2500-2900 | ||
| 2900-3300 | ||
| 3300-3700 | ||
| 3700-4100 | ||
| 4100-4500 | ||
| 4500-4900 |
1.Определить среднегодовой надой молока на 1 корову, кг;
2.Моду и медиану среднегодовой продуктивности коров, кг.
1) Для определения среднегодового надоя молока в целом по всем группам необходимо сначала перейти от интервального ряда к моментному: (Нижний+Верхний)/2
2) Найти моду и медиану- особые средние величины.
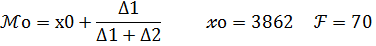
Сначала определим моду интервалов, т.е. тот интервал где частота наибольшая: 4100-4500
= 70 голов – частота мод интервалов
= 4500-4100=400
=70-27=43
=70-4=66
М=3862+400 * (43/(43+66))=4018
Мода = 4018 кг это наиболее часто встречающееся в совокупности значение среднегодового надоя молока на 1 корову.
Медиана расчитывается:

Сначала определим:
Сумму = 2+10+21+12+27+70+4=146
Находим полусумму
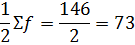
Определим сумму частот начиная с 1.
2+10+21+12+27+70>73
Последняя частота 70 является медианной частотой,а интервал в соответствии – медианным интервалом 4100-4500
fm- медианнаячастота 70
хо – нижняя граница медианного интервала =4100
ί – величина медианного интервала 400
Sm= 2+10+21+12+27=72
Me=4100+400  =4104 (кг)
=4104 (кг)
Медиана – 4104 кг это размер среднегодового надоя молока на 1 корову расположенная в середине ряда значений этого признака, построенного в порядке возрастания или убывания признаков.
Задача 47
Имеются показатели объема реализации продуктов на рынках города с января по май.
|
| Говядина, ц | 52,9 | 91,1 | 106,3 | 120,5 | 98,1 |
Решение:
| Показатели | Январь | Февраль | Март | Апрель | Май |
| Говядина,ц | 52.9 | 91.1 | 106.3 | 120.5 | 98.1 |
| 1)Абсолютный прирост · Базисный способ · Цепной способ | 0.0 0.0 | 38.2 38.2 | 53.4 15.2 | 67.6 14.2 | 45.2 -22.4 |
| 2)Темп роста % · Базисный способ · Цепной способ | 172.2 172.2 | 200.9 116.7 | 227.8 113.4 | 18.5 81.4 | |
| 3)Темп прироста% · Базисный способ · Цепной способ | 72.2 72.2 | 100.9 16.7 | 127.8 13.4 | -81.5 -18.6 | |
| 4)Абсолютное значение 1% прироста · Базисный способ · Цепной способ | - - | 0.5 0.5 | 0.5 0.9 | 0.5 | -0.6 |
Базисный способ
Цепной способ
Задача 58
| 11аимепоиание продукции | Товарооборот, тыс. руб. | Изменение цены в текущем периоде по сравнению с | ||
| базисный период | текущий период | |||
| 1 | 2 | 3 | 4 |
| Молоко Сметана Творог | 18,9 12,4 10,5 | 20,7 16,4 11,7 | -8,0 + 14,9 +2,7 |
1.Определите общие индексы цен, товарооборота и физического объема реализации.
2.Сделайте краткие экономические выводы.
| Продукция | Товарооборот,тыс.руб. | Изменение цены в текущий период по сравнению с базисным | |||
| базисный | текущий | Т прироста,% | Т роста, | ίр | |
| Молоко | 18.9 | 20.7 | -8.0 | 108.0 | 1.080 |
| Сметана | 12.4 | 16.4 | +14.9 | 114.9 | 1.149 |
| Творог | 10.5 | 11.7 | +2.7 | 102.7 | 1.027 |
1) Общий индекс цены
2) Общий индекс товарооборота
Товарооборот в текущем периоде по сравнению базиснымвозрасла на 17 %
3) Общий индекс количества продукции
Объем продажи продукции по сравнению с базиснымвозрасла на 7 %
Задача 69.
Требуется определить, сколько коров можно обследовать, исчислить средний годовой надой с возможной ошибкой (кг):22
При среднем квадратическом отклонении (кг): 420
Результат гарантировать с вероятностью 0,954.
Решение:
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 1757; Нарушение авторских прав?; Мы поможем в написании вашей работы!