Конечные элементы тонких пластин и пологих оболочек (КЭ 221-224, 227, 230, 241, 242, 244)

Предназначены для решения плоской задачи теории упругости (плоское напряженное состояние и плоская деформация), а также прочностного расчета тонких и пологих оболочек с учетом физической нелинейности материала.

Теоретические сведения о конечно-элементном подходе к решению задачи изгиба и плоской задачи теории упругости справедливы и для плоских физически-нелинейных конечных элементов.

Элементы матрицы жесткости определяются с использованием численного интегрирования в следующей форме:

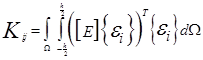, (7.3)

где: Ω -область конечного элемента;

[Е ] - матрица интегральных жесткостей k-го шага;

{e} - вектор деформаций.

Размерность и компоненты матрицы упругих характеристик зависят от типа конечного элемента. Матрица упругих характеристик конечного элемента плоской пологой оболочки (тип КЭ 241, 242 и 244) имеет вид, представленный в табл. 7.7.:

Таблица 7.7

F1	F2		C1	C2
F3	F4		C3	C4
		F5			C5
C1	C2		D1	D2
C3	C4		D3	D4
		C5			D5

где:

Fi- интегральные жесткости плоского напряженного состояния;

Di- интегральные жесткости задачи изгиба;

Сi- интегральные жесткости взаимовлияния этих двух состояний.

Интегральные жесткости вычисляются численным интегрированием по толщине оболочки с учетом наличия арматурных включений. Они зависят от положения точки в плане.

Например:

;

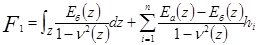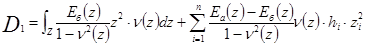; (7.4)

,

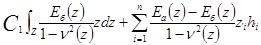где:

E_б(z) - модуль Юнга основного материала сечения (бетона);

E_а(z) - модуль Юнга армирующего материала;

ν(z) - коэффициент Пуассона в точке;

n - число арматурных включений по толщине сечения оболочки.

Конечные элементы плоской задачи (КЭ 221 ¸ 230) представляют собой частные случаи конечного элемента оболочки. Для них интегральные жесткости изгиба и взаимовлияния равны нулю. Для решения плоской задачи применяется шагово-итерационный метод.

Определение новых значений модуля Юнга и приведенного коэффициента Пуассона производится по выбранному пользователем закону деформирования материала (табл. 7.2), на основании определенной в данной точке обобщенной деформации:

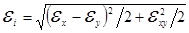, (7.5)

для оболочек и на основании ε₁, ε₂ для плоской задачи.

Определение прочности двухкомпонентного (железобетонного) элемента производится на каждом шаге приложения нагрузки по полученным напряжениям и деформациям в центре тяжести КЭ.

Проверяются условия прочности основного материала (бетона) по главным напряжениям (s₁, s₂) и деформациям (e₁, e₂) в соответствии с заданным законом деформирования материала. При этом фиксируется образование одиночных и перекрестных трещин или выкалывание материала при сжатии.

Прочность арматуры в элементе с трещинами определяется с учетом нагельного эффекта в соответствии с [6],при этом фиксируется текучесть, разрывы или смятие (срез) арматуры.

Для элементов бетонных и железобетонных стержней и оболочек определяется также прочность сечений в соответствии с действующими нормами.

Вся информация о состоянии КЭ на каждом шаге выдается в текстовый файл «Сведения о состоянии материала».

Дата добавления: 2017-01-14