Образец решения и оформления задач контрольной работы

Вариант 0

Задача 1. Вычислить:

Решение. Размерность первой матрицы , второй , тогда в произведении получится матрица размерностью (используйте схему, правило умножения двух матриц)

Ответ:  

Задача 2. Решить систему линейных уравнений методом Гаусса.

Решение. Составим расширенную матрицу и произведем элементарные преобразования над ней

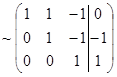Полученная матрица соответствует системе 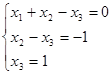. Осуществляя обратный ход, находим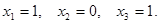

Ответ: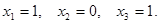

Решить систему линейных уравнений методом Крамера.

Решение. Найдем определитель системы и, если он не равен нулю, продолжаем вычисления. Можно применить формулу Крамера . Используем правило треугольников для вычисления определителя: 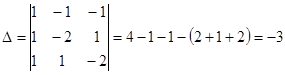. Определитель отличен от нуля. Вычислим три вспомогательных определителя, заменяя столбцом свободных членов поочередно столбцы основного определителя. Разложим определитель по элементам первого столбца, 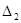по элементам второго столбца, по элементам третьего столбца:

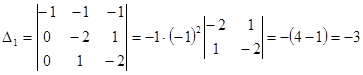
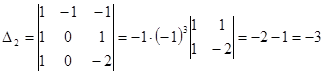
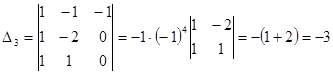
Подставляем найденные значения в формулу Крамера:

Ответ:

Задача 3

Записать число z в алгебраической и тригонометрической форме.

Решение. Алгебраическая форма записи числа имеет вид 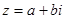, где и

Преобразуем 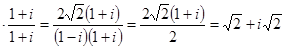, где

Тригонометрическая запись комплексного числа имеет вид:

, где . Найдем модуль комплексного числа

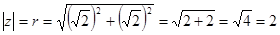. Найдем аргумент комплексного числа по формуле

; ; .

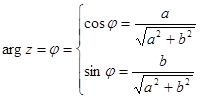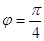Тогда тригонометрическая форма записи комплексного числа имеет вид: .

Ответ: Алгебраическая форма записи числа имеет вид , где 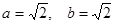Тригонометрическая форма записи комплексного числа имеет вид: .

Задача 4. Исследовать на непрерывность функцию и построить ее схему.

Решение:

1. Найдем область определения функции

Так как , то и область определения. В точке функция неопределенна и значит - точка разрыва.

2. Исследуем разрыв односторонними пределами:

, где означает, что 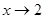слева, т.е остается меньше двух.

, где означает, что 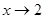справа.

Проведем дополнительные исследования при ; . Построим схему разрыва и график данной функции. Рис.1

Рис.1

Задача 5. Найти производные функций: 1) ,

2) , 3) , 4) , 5) .

Решение:

;

;

;

;

.

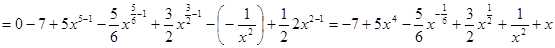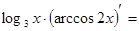
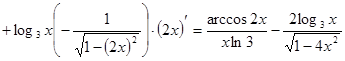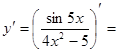
Задача 6. Найти пределы: ; ; ; .

Решение:

, т.к.

При величины , , , стремятся к нулю.

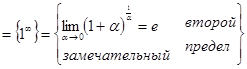
, при .

Ответ: , , ,

Задача 7. Исследовать функцию и построить ее график

Решение:

1. Область определения

2. Функция элементарная и определенна для всех х, значит, она непрерывна. Нет бесконечных разрывов, значит, нет вертикальных асимптот.

3. При 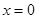, , 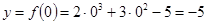точка пересечения с осью OY .

При , , , или 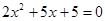, , 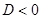точка пересечения с осью ОХ .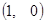

4. , , значит, функция не является четной или нечетной.

5. , , , 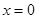или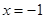

Итак: , ; , . Промежутки возрастания и убывания:

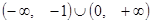- функция возрастает, - функция убывает.

6. , , 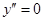, других точек подозрительных на перегиб нет, т.к. непрерывна.

Имеем одну точку перегиба:

7. Невертикальные асимптоты ;

, значит, невертикальных асимптот нет.

8. Контрольно-уточняющие точки: при , , при ,

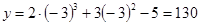
9. Строим чертеж

Рисунок.2

Задача 8. Найти площадь фигуры, ограниченной линиями:

.

Решение. Площадь данной фигуры равна разности площадей криволинейных трапеций, образованных прямой и гиперболой на отрезке .

.

Ответ:

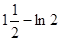
Задача 9. Решить дифференциальное уравнение

Решение. Составим характеристическое уравнение . Найдем корни и . Тогда общее решение дифференциального уравнения запишется в виде ()

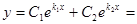
Ответ:

Задача 10. Исследовать на сходимость числовой ряд ;

Решение. Так как в записи общего члена ряда есть факториал (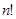), то используем признак Даламбера. Для исследуемого ряда

Вычислим

В пределе получили бесконечность, следовательно, исследуемый ряд расходится.

Воспользуемся радикальным признаком Коши. Здесь

Вычислим

Полученное значение больше 1, следовательно, ряд расходится.

Задача 11.

В цехе имеется n моторов. Вероятность того, что мотор в данный момент включен, равна h. Найти вероятность, что в данный момент:

а) включено 4 мотора

б) включены все моторы

в) выключены все моторы

Решение.

Формула Бернулли. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р , событие наступит ровно k раз (безразлично, в какой последовательности), равна:

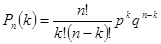или , где .

а) ; ; ;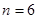

б) ; ; ; ;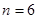

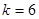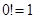в) ; ; ;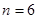

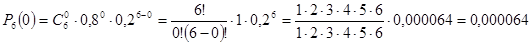
Ответ: а) 0,246; б) 0,2624; в) 0,000064

Дата добавления: 2017-01-14