Интернет-ресурсы 2 страница

.

Пряма у просторі. Канонічне рівняння прямої у просторі визначається умовою паралельності деякого вектора (напрямний вектор прямої) та довільного вектора , що належить прямій:

.

Якщо ввести параметр , то будемо мати параметричне рівняння прямої:

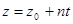; ; , де - будь-яке дійсне число.

Рівняння прямої, що проходить через 2 точки М₁(x₁;y₁;z₁) та М₂(x₂;y₂;z₂), має вигляд:

.

Іноді рівняння прямої розглядається як перетин двох площин

.

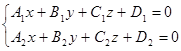Канонічне рівняння отримаємо, якщо послідовно виключити з системи невідомі та .

Умови паралельності і перпендикулярності прямих, а також прямої і площини витікають з відповідних властивостей напрямних векторів, напрямного та нормального векторів.

Кут між прямою і площиною знаходимо за формулою

, де , .

Криві другого порядку на площині. Маємо 4 види кривих другого порядку на площині: коло, еліпс, гіпербола і парабола.

Коло – геометричне місце точок, рівновіддалених від даної точки, що називається центром кола. Рівняння кола: 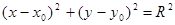, де - поточні координати, - координати центра, 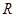- радіус кола.

Еліпс – геометричне місце точок, сума відстаней яких від двох заданих точок (фокуси еліпса) є величина стала.

Рівняння еліпса: , де - поточні координати, та - велика і мала півосі.

Ексцентриситет еліпса: , де - відстань між фокусами еліпса. Маємо співвідношення .

Гіпербола – геометричне місце точок, різниця відстаней яких від двох заданих точок, що називаються фокусами, є величина стала.

Рівняння гіперболи: , де - поточні координати, та - велика і мала півосі.

Ексцентриситет гіперболи: . Прямі називаються асимптотами гіперболи.

Парабола – геометричне місце точок, рівновіддалених від даної точки (фокуса) і даної прямої (директриси).

Рівняння параболи: , де - параметр параболи. Ексцентриситет параболи .

Маємо чотири види параболи з вісями симетрії по Ох та Оy.

Поверхні другого порядку. Основним методом дослідження форми поверхонь за їх рівняннями є метод перерізів, який полягає у наступному:

1) знаходять перерізи поверхонь з кожною координатною площиною ();

2) знаходять перерізи поверхонь з площинами, паралельними координатним площинам ();

3) за отриманими кривими роблять висновок про форму поверхні;

4) виконують схематичний малюнок поверхні.

Для висновків маємо наступний перелік поверхонь: куля, еліпсоїд, еліптичний та гіперболічний параболоїди, однополосний та двополосний гіперболоїди, конус, циліндр.

Рівняння та малюнки поверхонь можна подивитися у довіднику з вищої математики.

Завдання №1 (варіанти завдань у таблиці 3.1). У трикутнику АВС потрібно знайти:

1) рівняння сторони ВС;

2) величину кута при вершині А;

3) рівняння і довжину висоти до сторони ВС;

4) рівняння і довжину медіани до сторони ВС;

5) рівняння бісектриси кута при вершині А;

6) площу трикутника АВС.

Завдання №2 (варіанти завдань у таблиці 3.2).

Скласти рівняння лінії, відстань кожної точки якої від точки М₀(x₀;y₀) і від прямої або 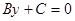відносяться як . Зобразити лінію на малюнку.

Завдання №3 (варіанти завдань у таблиці 3.3). Задані координати вершин піраміди . Потрібно знайти:

1) рівняння ребер та та їх довжини;

2) кут між ребрами та ;

3) рівняння грані ;

4) кут між ребром та гранню ;

5) довжину висоти , проведеної з вершини на грань ;

6) рівняння висоти ;

7) координати точки перетину висоти з гранню ;

8) координати точки, яка симетрична точці відносно грані ;

9) рівняння площини, що проходить через А₁А₄ перпендикулярно площині А₁А₂А₃.

Таблиця 3.1 Таблиця 3.2

Варі-ант	А(х1; у1)	В(х2; у2)	С(х3; у3)		Варі-ант	Рівняння прямої	М0­(х0; у0)	m:n
1.	(0;-2)	(1; 1)	(–2; 1)		1.	2x–3=0	(1; 1)	3:2
2.	(0; 1)	(1; –1)	(1; 0)		2.	x+2=0	(–1; 0)	2:3
3.	(1; 0)	(1; –2)	(–1; 1)		3.	y–2=0	(1; 2)	1:1
4.	(2; 1)	(2; 2)	(3; 1)		4.	1/2y+4=0	(–2; 4)	1:2
5.	(3; 0)	(3; 2)	(4; 1)		5.	x–1=0	(–1; 1)	2:1
6.	(–1; 3)	(–1; –2)	(1; 1)		6.	2x+1=0	(0; 2)	5:6
7.	(0; 1)	(1; 1)	(2; –1)		7.	2y–3=0	(2; 0)	3:4
8.	(2; 2)	(8; 3)	(–1; –1)		8.	3y+5=0	(3; 1)	1:2
9.	(4; 7)	(2; 5)	(0; 0)		9.	y–1=0	(–1; 2)	2:3
10.	(3; 2)	(–3; 0)	(0; 4)		10.	x+1=0	(2; 4)	3:5
11.	(2; 3)	(1; –1)	(6; 4)		11.	x–5=0	(1; –1)	1:1
12.	(7; –1)	(–3; 2)	(2; 7)		12.	y+1=0	(6; 5)	2:1
13.	(3; –4)	(10; 1)	(0; 7)		13.	x–2=0	(4; 3)	3:2
14.	(–1; –3)	(–5; 4)	(2; 9)		14.	3x+4=0	(2; 1)	2:3
15.	(2; 1)	(1; 1)	(3; –5)		15.	x+2=0	(0; –1)	1:1
16.	(4; 6)	(–4; 6)	(–1; 0)		16.	3x–1=0	(0; 1)	1:1
17.	(2; 8)	(–2; 4)	(3; 1)		17.	y+2=0	(1; 1)	6:5
18.	(1; –1)	(0; 1)	(2; 1)		18.	y–1=0	(1; –2)	2:1
19.	(0; 2)	(–1; 1)	(2; 4)		19.	y–5=0	(1; 1)	5:3
20.	(9; 3)	(7; 1)	(–2; 5)		20.	2x+3=0	(1; 2)	2:3
21.	(0; 4)	(0; 0)	(–1; 2)		21.	y–1=0	(–1; –1)	1:2
22.	(5; 3)	(3; 8)	(0; 7)		22.	x+1=0	(1; 4)	1:2
23.	(6; 9)	(–4; 0)	(7; 1)		23.	2x–3=0	(1; 3)	1:1
24.	(2; 9)	(10; 1)	(0; –5)		24.	x–8=0	(1; 1)	4:3
25.	(–1; 2)	(3; 7)	(1; 2)		25.	x–3=0	(–1; 1)	2:1
26.	(7; 1)	(9; 3)	(–2; 5)		26.	3x+4=0	(2; 1)	2:3
27.	(3; –5)	(2; 1)	(1; 1)		27.	y+2=0	(1; 1)	6:5
28.	(0; 7)	(3; –4)	(10; 1)		28.	x+1=0	(1; 4)	1:2
29.	(–2; 4)	(2; 8)	(3; 1)		29.	y–1=0	(1; –2)	2:1
30.	(–4; 0)	(7; 1)	(6; 9)		30.	x–2=0	(4; 3)	3:2

Таблиця 3.3

Варі-ант	А1(x1; y1; z1)	А2(x2; y2; z2)	А3(x3; y3; z3)	А4(x4; y4; z4)
1.	(1; 3; 6)	(2; 2; 1)	(–1; 0; 1)	(–4; 6; –7)
2.	(–4; 2; 6)	(2; –3; 0)	(–10; 5; 8)	(–5; 2; –4)
3.	(7; 2; 4)	(7; –1; –2)	(3; 3; 1)	(–4; 2; 8)
4.	(2; 1; 4)	(–1; 5;–2)	(–7; –3; 2)	(–6; –3; 6)
5.	(–1; –5; 2)	(–6; 0; –3)	(3; 6; –3)	(–10; 6; 7)
6.	(0; –1; 1)	(–2; 3; 5)	(1; –5; –9)	(–1; –6; 3)
7.	(5; 2; 0)	(2; 5; 0)	(1; 2; 4)	(–1; 1; 1)
8.	(2; –1; –2)	(1; 2; 1)	(5; 0; –6)	(–10; 9; –7)
9.	(–2; 0; –4)	(–1; 7; 1)	(4; –8; –4)	(1; –4; 6)
10.	(14; 4; 5)	(–5; –3; 2)	(–2; –6; –3)	(–2; 2; –1)
11.	(1; 2; 0)	(3; 0; –3)	(5; 2; 6)	(8; 4; –9)
12.	(2; –1; 2)	(1; 2; –1)	(3; 2; 1)	(–4; 2; 5)
13.	(1; 1; 2)	(–1; 1; 3)	(2; –2; 4)	(–1; 0; –2)
14.	(2; 3; 1)	(4; 1; –2)	(6; 3; 7)	(7; 5; –3)
15.	(1; 1; –1)	(2; 3;1)	(3; 2; 1)	(5; 9; –8)
16.	(1; 5; –7)	(–3; 6; 3)	(–2; 7; 3)	(–4; 8; –12)
17.	(–3; 4; –7)	(1; 5; –4)	(–5; –2; 0)	(2; 5; 4)
18.	(–1; 2; –3)	(4; –1; 0)	(2; 1; –2)	(3; 4; 5)
19.	(4; –1; 3)	(–2; 1; 0)	(0; –5; 1)	(3; 2; –6)
20.	(1; –1; 1)	(–2; 0; 3)	(2; 1; –1)	(2; –2; –4)
21.	(1; 2; 0)	(1; –1; 2)	(0; 1; –1)	(–3; 0; 1)
22.	(1; 0; 2)	(1; 2; –1)	(2; –2; 1)	(2; 1; 0)
23.	(1; 2; –3)	(1; 0; 1)	(–2; –1; 6)	(0; –5; –4)
24.	(3; 10; –1)	(–2; 3; –5)	(–6; 0; –3)	(1; –1; 2)
25.	(–1; 2; 4)	(–1; –2; –4)	(3; 0; –1)	(7; –3; 1)
26.	(1; 2; 0)	(1; 2; –1)	(–5; –2; 0)	(–3; 0; 1)
27.	(3; 10; –1)	(1; 5; –4)	(–2; 7; 3)	(2; 5; 4)
28.	(3; 4; 5)	(2; 1; –2)	(4; –1; 0)	(–1; 2; –3)
29.	(2; –2; 1)	(1; 2; –1)	(1; 0; 2)	(2; 1; 0)
30.	(2; 3;1)	(1; 1; –1)	(5; 9; –8)	(3; 2; 1)

Завдання №4: звести до канонічного виду рівняння поверхонь, заданих у таблицях 3.4 та 3.5; методом перерізів провести дослідження і побудувати ці поверхні.

Таблиця 3.4 Таблиця 3.5

Варі-ант	Рівняння поверхонь		Варі-ант	Рівняння поверхонь
1.	х^2+у^2+z^2=6x–4z		1.	x^2–4y^2=16z
2.	x^2+y^2+z^2–3x+6y+2z–5=0		2.	z=x^2+y^2–6y+10
3.	x^2+y^2+z^2–2x+4y–6z–22=0		3.	x^2+y^2=(z+1)
4.	x^2–3y^2+2z^2+2x–6y+4z=0		4.	4x^2–9y^2=36z
5.	x^2+y^2+z^2–12x+4y–6z=0		5.	x^2+y^2–2x–2y–4z+2=0
6.	2x^2+y^2+2z^2–4x+4y+4z+7=0		6.	x^2+2x+y^2–6y–6=0
7.	x^2–y^2+4z^2–10x+6y–16z+16=0		7.	x^2+y^2–2x+2y+2=z
8.	x^2+y^2+4z^2–2x–15=0		8.	z=4–y^2
9.	3x^2+3y^2–3z^2–6x+4y+4z+3=0		9.	y^2+z^2=x^2
10.	x^2–6y^2+3z^2+8x+12y+1=0		10.	z=x^2+2
11.	x^2+4y^2+9z^2–6x+8y–18z–14=0		11.	x^2+(y–1)^2=z^2
12.	3x^2+3y^2+3z^2–6x+4y–1=0		12.	y^2+z^2–x–4=0
13.	x^2+y^2+z^2–2x–2y–2z–1=0		13.	x^2+z^2–4y=0
14.	2x^2–y^2+z^2+4x+2y+8z+1=0		14.	x^2+y^2–2z=0
15.	3x^2–4y^2–6x+8y–z^2+11=0		15.	x^2+z^2–y–1=0
16.	x^2+y^2+z^2–8z+12=0		16.	x^2+3y^2–3z+3=0
17.	x^2+2y^2–3z^2+2x+4y–6z=0		17.	2x^2–2+2=0
18.	2x^2+2y^2+2z^2–5y–8=0		18.	x^2+y^2+2x–6y+10=z
19.	x^2+4y^2–z^2–10x–16y+6z+16=0		19.	(x–1)^2+z^2=y^2
20.	x^2+y^2+4z^2+2x–4y+2=0		20.	2y^2–z–2=0
21.	2x^2+3y^2+z^2+6y–9=0		21.	z=9–x^2
22.	4x^2–4y^2+4z^2+2x–6y+8z–5=0		22.	4x^2–y^2=16z
23.	x^2+3y^2+3z^2+2x–8=0		23.	(y+2)^2+z^2=x^2
24.	2x^2+3y^2+4z^2–4x+6y–7=0		24.	x^2+4z^2–16y+16=0
25.	x^2+y^2+z^2–4z=0		25.	x^2+z^2–2x–2z–7=0
26.	3x^2+3y^2+z^2–6x+6y–3=0		26.	z=y^2–4
27.	x^2+2y^2+z^2–6x+1=0		27.	x^2–9y^2=9z
28.	4x^2+y^2+4z^2–2y–15=0		28.	y^2+z^2=(x–1)^2
29.	3x^2+2y^2+z^2–6x–9=0		29.	x^2+z^2–y+1=0
30.	x^2+y^2+z^2–6x=0		30.	2x^2+3y^2–4x+6y–13=0

ПЕРЕЛІК НАВЧАЛЬНО-МЕТОДИЧНОЇ ЛІТЕРАТУРИ

1. Міхайленко В.М., Овчинніков П.П., Яремчук Ф.П. “ Вища математика”, ч.1,2. -Київ:

“Техніка”, 2000р.

2. Журавель О.О. Вища математика. Збірник завдань для курсових і самостійних робіт. -

Київ,1998р.

3. Клетеник Д.В. Сборник задач по аналитической геометрии. -М.: Наука, 1964.

4. Сборник задач по математике для втузов. Линейная алгебра и основы математического

анализа. Под редакцией Ефимова А.В. и Демидовича Б.М.-М.: Наука, 1981.

5. Каплан И.А. Практические занятия по высшей математике.- Из-во Харьковского

университета, 1972.

6. Бугров Я.С., Никольский С.М. - Элементы линейной алгебры и аналитической геометрии.-М.:

Наука, 1980.

http://www.hist.msu.ru/ER/Etext/list.htm – электронная библиотека исторического факультета МГУ им. М.В. Ломоносова. Представлены источники по всему курсу отечественной и всеобщей истории.

http://fershal.narod.ru – проект “Российский мемуарий” – воспоминания, дневники XVIII – начала XX в.

http://hronos.km.ru – проект “Хронос” – хронологические таблицы, схемы, письменные источники по российской истории

http://old-rus.narod.ru – историко-литературный сайт “Древнерусская литература” - наряду с древнерусскими текстами представлены материалы по истории духовной и художественной культуры средневековой Руси, в том числе, по истории Русской православной церкви.

http://www.museum.ru/museum/1812/Library/index.html – библиотека проекта «1812 г.» - представлены источники, исследования, литературные памятники, произведения изобразительного искусства, повествующие о событиях Отечественной войны 1812 г.

http://decemb.hobby.ru – проект “Виртуальный музей декабристов” - собрание воспоминаний участников декабристского движения, программные документы декабристов.

http://www.magister.msk.ru/library/history/history1.htm – сайт “Материалы по русской истории” - электронная версия сочинений дореволюционных российских историков: В.Н. Татищева, Н.М. Карамзина, С.М. Соловьёва, В.О. Ключевского, С.Ф. Платонова.

http://www.ostu.ru/personal/nikolaev/index.html – проект “Геосинхрония” – крупнейший на сегодняшний день массив электронных, интерактивных и анимированных исторических карт.

http://www.historia.ru / - На сайте размещен российский электронный журнал «Мир истории».

http://www.hrono.ru / libris / lib_p/index.html - Сайт содержит электронную версию

курса лекций по русской истории С.Ф.Платонова.

http://historydoc.edu.ru - Российский общеобразовательный портал. Коллекция: исторические документы.

http: rushistory.stsland.ru/ - Сайт содержит статьи по истории России, тексты

исторических документов, термины и даты по истории России.

http://rulers.narod.ru/ - Всемирная история в лицах.

http://www.hronos.km.ru/ - Хронос. Всемирная история в Интернете

http://www.humanities.edu.ru/ - Портал «Гуманитарное образование».

Дата добавления: 2017-01-14