Пояснения к работе

ОПРЕДЕЛЕНИЕ КОРРЕЛЯЦИОННЫХ ЗАВИСИМОСТЕЙ МЕЖДУ ГЕОФИЗИЧЕСКИМИ ПАРАМЕТРАМИ И ФИЗИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ ГОРНЫХ ПОРОД

Практическое занятие № 3

Методические указания

Рассчитать коэффициент абсолютной проницаемости породы (значения величин, необходимых для расчета, определены путем пропускания воздуха сквозь образец). Данные лабораторного опыта приведены в таблице.

Таблица 3

Варианты заданий	Диаметр образца d, см	Длина образца породы L, см	Объём профильтрованного сквозь образец воздуха Ve,, см^3	Время фильтрации воздуха t, с	Динамическая вязкость воздуха m, мПа*с	Давление на входе в образец рвх, 10^5Па	Давление на выходе из образца р вых ,10^5Па
	3,1	4,1			0,016	1,7	1,2
	3,0	3,2			0,018	1,3
	2,9	3,6			0,019	1,5
	2,6	2,8			0,017	2,2	1,6
	3,2	2,7			0,018	2,1	1,7
	3,3	3,0			0,018	2,2	1,9
	3,6	3,2			0,02	2,3	1,9
	3,8	3,3			0,02	2,5	2,1
	4,1	3,5			0,02	2,5	2,3
	4,2	3,8			0,022	2.8	2,5

Цель работы: изучение теоретических основ определения корреляционных связей между геофизическими параметрами и физическими характеристиками горных пород.

Материалы и принадлежности: массив данных об измеренных физических свойствах пород; линейка; микрокалькулятор.

При геологических, гидрогеологических и инженерно-технических изыскани­ях возникает необходимость определять пористость, трещиноватость, прочностные параметры, водонасыщенность и другие физи­ко-механические и коллекторские свойства горных пород. Теоретические и экспериментальные исследования позволяют уста­новить связь между этими параметрами ифизическими свойст­вами пород, определяемыми при геофизических исследованиях как в лабораторных условиях на образцах, так ив естественном зале­гании пород.

С помощью корреляционного анализа оценивается степень бли­зости корреляционной зависимости к функциональной, которая ха­рактеризуется коэффициентом корреляции

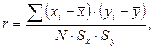
где 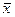- среднее значение х; - среднее значение у; N – число измерений; S_x, S_y – средние квадратические отклонения:

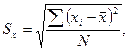
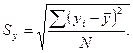
Коэффициент корреляции r изменяется от -1 до +1. При r = 0 линейная связь между х и у отсутствует, а при r = ±1 связь меж­ду х и у функциональная.

Путем корреляционного анализа определяется характер свя­зей и уравнение регрессии

Эмпирическое распределение двух величин может быть пред­ставлено в виде поля корреляции, на котором могут быть даны линии регрессии. На рис. 11.1, а показаны поле корреляции, линия регрессии плотности и скорости распространения продольных волн (коэффициент корреляции положительный – с увеличением одной величины другая тоже возрастает); на рис. 11.1 ,б представлено поле корреляции, линия регрессии плотности базальтов Армении и пористости (коэффициент корреляции отрицательный – с увеличением одной величины другая уменьшается).

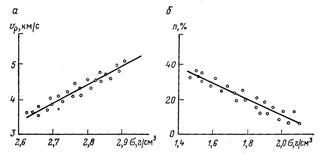
Рис. 11. 1. Поле корреляции и линия регрессии скорости распространения упругих волн, плотности и пористости: а - коэффициент корреляции положительный; б – коэффициент корреляции отрицательный

Физические свойства горных пород могут быть связаны между собой не только линейной, но и более сложной зависимостью – в этом случае речь идет о нелинейной корреляции (например, ломаная регрессия, криволинейные уравнения корреляционной свя­зи и т. д.).

При геофизических исследованиях нередко бывает, что интере­сующий нас параметр зависит от двух и даже большего числа дру­гих параметров. Корреляция таких величин называется множественной.

Статистическую обработку большого числа измерений физиче­ских параметров образцов и установление сложных корреляцион­ных зависимостей целесообразно проводить с помощью ЭВМ.

Пример 11.1. Составить линейное корреляционное уравнение и оценить тесноту связи между значениями коэффициента Пуассона n и скоростью распростране­ния продольных волн V_p для диабазов. Исходные данные для составления урав­нения и результаты расчетов приведены в табл. 11.1.

Для того чтобы составить уравнение регрессии и вычислить коэффициент корреляции, надо определить для имеющихся значений х и у следующие величины:

1) среднее значение ;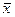

2) среднее значение ;

3) для каждого значения x_i его отклонение от среднего значения 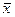, т. е. 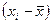, и квадрат этого отклонения ;

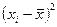4) для каждого значения y_i его отклонение от среднего значения , т. е. , и квадрат этого отклонения ;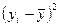

Таблица 11.1

№ п/п	x (Vp), км/с	y (n)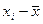
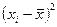
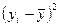
	5.1 6.1 7.1 4.2 4,1 4,8 5,1 5,0 5,3 5,9 7,0 6,9 6,7 6,1 6,0 4,7 4,6 6,1 4,2 4,8 5,0 5,9 6,7 5,3 6,0	0,22 0,31 0,34 0,16 0,12 0,18 0,17 0,21 0,23 0,24 0,33 0,31 0,30 0,29 0,28 0,24 0,22 0,31 0,16 0,18 0,21 0,24 0,30 0,23 0,28	-0,47 0,53 1,53 -1,37 -1,47 -0,77 -0,47 -0,57 -0,27 0,33 1,43 1,33 1,13 0,53 0,43 -0,87 -0,97 0,53 -1,37 -0,77 -0,57 0,33 1,13 -0,27 0,43	-0,20 0,07 0,10 -0,08 -0,12 -0,06 -0,07 -0,03 -0,01 0,00 0,09 0,07 0,06 0,05 0,04 0,00 -0,02 0,07 -0,08 -0,06 -0,03 0,00 0,06 20,01 0,04	0,22 0,28 2,34 1,87 2,16 0,59 0,22 0,32 0,07 0,11 2,04 1,77 1,27 0,28 0,18 0,76 0,94 0,28 1,87 0,59 0,32 0,11 1,27 0,07 0,18	0,0400 0,0049 0,0100 0,0064 0,0144 0,0036 0,0049 0,0009 0,0001 0,0000 0,0081 0,0049 0,0036 0,0025 0,0016 0,0000 0,0004 0,0049 0,0064 0,0036 0,0009 0,0000 0,0036 0,0001 0,0016	0,094 0,037 0,153 0,110 0,180 0,046 0,033 0,017 0,0003 0,0000 0,130 0,090 0,068 0,027 0,017 0,000 0,019 0,037 0,110 0,046 0,017 0,000 0,068 0,0003 0,017

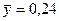
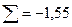
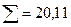
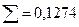
5) для каждого значения x_i и y_i произведение их отклонения от среднего, т. е. ;

6) сумму ;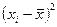

7) сумму ;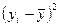

8) сумму ;

9) среднеквадратичное отклонение S_x = 0,890;

10) среднеквадратичное отклонение S_y = 0,071;

11) коэффициент корреляции r = 0,83;

а также составить уравнение регрессии

При r = 0,83, имея уравнение регрессии и зная скорость распространения продольных волн, можно оценить коэффициент Пуассона.

Вариант 1

Определить коэффициент корреляции и уравнение регрессии для эмпирической зависимости между динамическим модулем упругости (модулем Юнга) и скоростью распространения продольных волн в меловых известняках района Ингури ГЭС (табл. 11.3).

Таблица 3

x (Vp)	y (Ед)	x (Vp)	y (Ед)	x (Vp)	y (Ед)
1.5 1.8 3.1 4.1 1.9 2.5 3.5		3.3 1.6 2.9 2.8 3.0 3.0 4.6		2.9 2.8 3.7 4.1 4.2 2.1 -	-

Вариант 2

Определить коэффициент корреляции и уравнение регрессии для эмпирической зависимости между коэффициентом Пуассона и скоростью рас­пространения продольных волн в диабазах района Усть-Илимской ГЭС (табл. 11.4).

Таблица 11.4

x (Vp)	y (n)	x (Vp)	y (n)	x (Vp)	y (n)	x (Vp)	y (n)
4,2 6,1 7,1 5,0 5,5	0,20 0,28 0,32 0,25 0,27	6,5 4,5 4,7 4,3 5,8	0,30 0,21 0,23 0,20 0,27	6,1 6,4 6,6 7,0 4,2	0,28 0,29 0,30 0,31 0,20	4,5 4,8 4,9 6,6 5,1	0,22 0,24 0,24 0,30 0,25

Вариант 3

Определить коэффициент корреляции и уравнение регрессии для эмпирической зависимости между модулем упругости (модулем Юнга) и удельным электрическим сопротивлением для диабазов района Братской ГЭС (табл. 11.5).

Таблица 11.5

x (ρ)	y (Ед)	x (ρ)	y (Ед)	x (ρ)	y (Ед)	x (ρ)	y (Ед)

Вариант 4

Определить коэффициент корреляции и уравнение регрессии для эмпирической зависимости магнитной восприимчивости хромитовых руд от содержания в них хромита Cr₂O₃ (табл. 11.6).

Таблица 11.6

x (χ)	y (Cr2O3)	x (χ)	y (Cr2O3)	x (χ)	y (Cr2O3)
				-	-

Вариант 5

Определить коэффициент корреляции и уравнение регрессии для эмпирической зависимости плотности от пористости для базальтов Армении (табл. 11.7).

Таблица 11.7

x (п)	y (s)	x (п)	y (s)	x (п)	y (s)
	1,61 1,68 1,79 2,11 2,04 1,71 1,89		1,62 1,67 1,59 2,21 2,09 1,78 1,81	-	1,80 1,72 1,80 1,71 1,89 2,11 -

Вариант 6

Определить коэффициент корреляции и уравнение регрессии для эмпирической зависимости плотности s титаномагнетитовых руд от содержания в них железа (по материалам Уральского геологического управления по Первоуральскому месторождению; Fe₃О₄ – 75 %, FeTiO₂ – 25 % (табл. 11.8).

Таблица 11.8

x (Fe3О4, FeTiO2)	y (s)	x (Fe3О4, FeTiO2)	y (s)	x (Fe3О4, FeTiO2)	y (s)
	4,2 4,0 3,2 3,05 3,35 4,25 4,01 3,5		4,01 3,15 4,4 4,5 3,75 3,2 3,3	-	4,4 4,05 3,3 3,4 3,5 4,6 4,1 -

Вариант 7

Определить коэффициент корреляции и уравнение регрессии дляэмпирической зависимости плотности песчано-глинистых пород от их пористости (по И. X. Юдборовскому), табл. 11.9.

Таблица 11.9

x (s)	y (п)	x (s)	y (п)	x (s)	y (п)
2,30 1,65 1,92 2,05 2,50 1,95 2,20		2,00 1,66 1,78 2,00 1,97 1,95 2,40		2,1 2,2 1,9 1,7 1,8 2,0 -	-

Вариант 8

Определить коэффициент корреляции и уравнение регрессии для эмпирической зависимости плотности s титаномагнетитовых руд от содержания в них железа (по материалам Уральского геологического управления по Первоуральскому месторождению; Fe₃О₄ – 75 %, FeTiO₂ – 25 % (табл. 11.8).

Таблица 11.8

x (Fe3О4, FeTiO2)	y (s)	x (Fe3О4, FeTiO2)	y (s)	x (Fe3О4, FeTiO2)	y (s)
	4,2 4,0 3,2 3,05 3,35 4,25 4,01 3,5		4,01 3,15 4,4 4,5 3,75 3,2 3,3	-	4,2 4,0 3,2 3,05 3,35 4,25 4,01 3,5

Вариант 9

Определить коэффициент корреляции и уравнение регрессии для эмпирической зависимости магнитной восприимчивости хромитовых руд от содержания в них хромита Cr₂O₃ (табл. 11.6).

Таблица 11.6

x (χ)	y (Cr2O3)	x (χ)	y (Cr2O3)	x (χ)	y (Cr2O3)
				-	-

Вариант 10

Определить коэффициент корреляции и уравнение регрессии для эмпирической зависимости между модулем упругости (модулем Юнга) и удельным электрическим сопротивлением для диабазов района Братской ГЭС (табл. 11.10).

Таблица 11.10

x (ρ)	y (Ед)	x (ρ)	y (Ед)	x (ρ)	y (Ед)	x (ρ)	y (Ед)

Дата добавления: 2017-02-01