Свойства вейвлет-преобразования /3, 1/.

Результаты вейвлет-преобразования, как скалярного произведения вейвлета и сигнальной функции, содержат комбинированную информацию об анализируемом сигнале и самом вейвлете. Получение объективной информации о сигнале базируется на свойствах вейвлет-преобразования, общих для вейвлетов всех типов. Рассмотрим основные из этих свойств. Для обозначения операции вейвлет-преобразования произвольных функций s(t) будем применять индекс TW[s(t)].

Линейность.

TW[a·s₁(t)+b·s₂(t)] = a·TW[s₁(t)]+b·TW[s₂(t)]. (2.2.1)

Для векторных функций из этого следует, что TW векторной функции есть вектор с компонентами TW каждой из компонент анализируемого вектора в отдельности.

Инвариантность относительно сдвига. Сдвиг сигнала во времени на t₀ приводит к сдвигу вейвлет-спектра также на t₀:

TW[s(t-t_o)] = C(a, b-t_o). (2.2.2)

Инвариантность относительно масштабирования. Растяжение (сжатие) сигнала приводит к сжатию (растяжению) вейвлет-спектра сигнала:

TW[s(t/а_o)] = (1/а_о)·C(a/а_о,b/а_o). (2.2.3)

Дифференцирование.

dⁿ{TW[s(t)]}/dtⁿ = TW[dⁿ(s(t))/dtⁿ]. (2.2.4)

TW[dⁿ(s(t))/dtⁿ] = (-1)ⁿ s(t) [dⁿ(y(t))/dtⁿ] dt. (2.2.5)

Отсюда следует, что безразлично, дифференцировать ли функцию или анализирующий вейвлет. Если анализирующий вейвлет задан формулой, то это может быть очень полезным для анализа сигналов. Проанализировать особенности высокого порядка или мелкомасштабные вариации сигнала s(t) с игнорированием крупномасштабных полиномиальных составляющих (тренда и регионального фона) можно дифференцированием нужного числа раз либо вейвлета, либо самого сигнала. Это свойство особенно полезно, когда сигнал задан дискретным рядом.

Аналог теоремы Парсеваля для ортогональных и биортогональных вейвлетов.

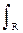s₁(t)·s₂*(t) = C_y^-1 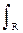a^-2 С(a,b) С*(a,b) da db. (2.2.6)

Отсюда следует, что энергия сигнала может вычисляться через коэффициенты вейвлет-преобразования.

Определения и свойства одномерного непрерывного вейвлет-преобразования обобщаются на многомерный и на дискретный случаи.

Дата добавления: 2017-02-01