Построить горизонтальную проекцию треугольника АВС. Угол наклона плоскости треугольника к фронтальной плоскости равен 30°, а сторона АВ параллельна фронтальной плоскости проекций.

7. Определить натуральную величину плоскости ABCD и углы ее наклона к горизонтальной (Ðα) и фронтальной (Ðβ) плоскостям проекций.

8. Построить недостающие проекции точек в системах плоскостей , ,

9. Определить какая из точек К или D принадлежит заданной плоскости.

10. На отрезке АВ найти точку, отстоящую от точки А на 30 мм.

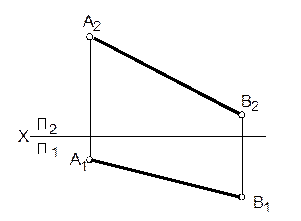
11. Построить горизонтальную проекцию отрезка DK, если угол его наклона (β) к фронтальной плоскости проекций равен 30°.

12. Построить проекции точки В, если В Î а и |АВ| = 30 мм.

а)

б)

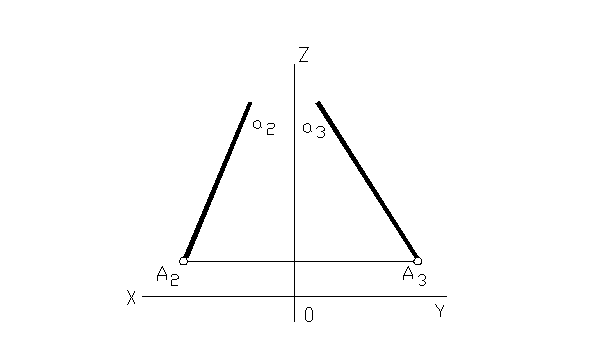
13. Достроить проекции треугольника BDE, лежащего в плоскости ∑ (ℓ×k).

14. Построить недостающие проекции плоского пятиугольника. В плоскости пятиугольника провести диагонали и определить их положение относительно плоскостей проекций.

Раздел 2. ПОВЕРХНОСТИ.

Подраздел 2.1. Гранные поверхности. Принадлежность точки и линии поверхности. Пересечение гранных поверхностей плоскостями частного положения. Определение натуральной величины фигуры сечения.

1. Построить недостающие проекции точек и линий, принадлежащих граням и ребрам призмы.

а) прямая призма.

Построить профильную проекцию. Определить натуральную величину фигуры сечения.

б) наклонная призма

2. Построить горизонтальную и профильную проекции пирамиды, усеченной плоскостями.

3. Построить горизонтальную и профильную (д: фронтальную) проекции пирамиды со сквозным призматическим отверстием.

а)

б)

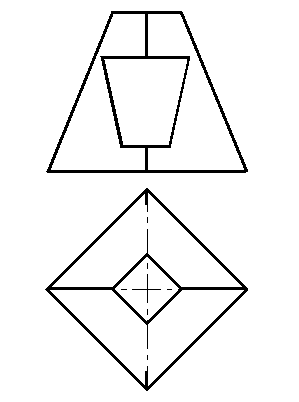
в)

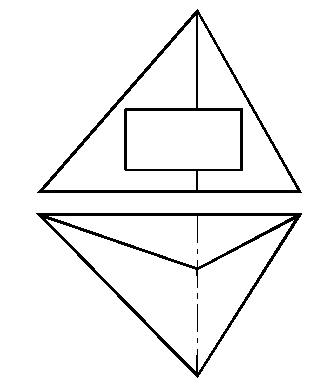
г)

д)

4. Построить недостающие проекции пирамиды, усеченной плоскостью ∑. Определить натуральную величину фигуры сечения.

5. Построить горизонтальную и профильную проекции модели, усеченной плоскостью ∑, и натуральную величину фигуры сечения.

Подраздел 2.2. Поверхности вращения. Линейчатые поверхности. Принадлежность точки и линии поверхности. Определение натуральной величины фигуры сечения.

1. Построить недостающие проекции линий, принадлежащих поверхности

а) наклонного цилиндра. Определить натуральную величину фигуры сечения.

б) прямого профильно-проецирующего цилиндра. Построить горизонтальную проекцию цилиндра и линий ему принадлежащих.

2. Построить фронтальную проекцию линии ℓ на боковой поверхности цилиндра.

3. Построить горизонтальную проекцию линии ℓ на боковой поверхности цилиндра.

4. Построить профильную проекцию цилиндра с отверстием и прорезями.

5. Построить профильную проекцию тела, проекции и натуральную величину сечения тела плоскостью ∑.

6. Построить горизонтальную и профильную проекции конуса, усеченного плоскостями.

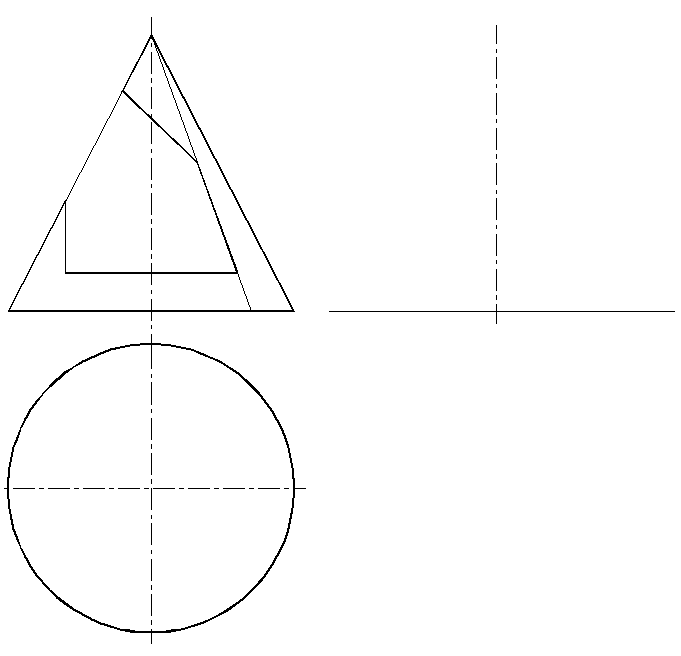
7. Построение сечений конуса плоскостью.

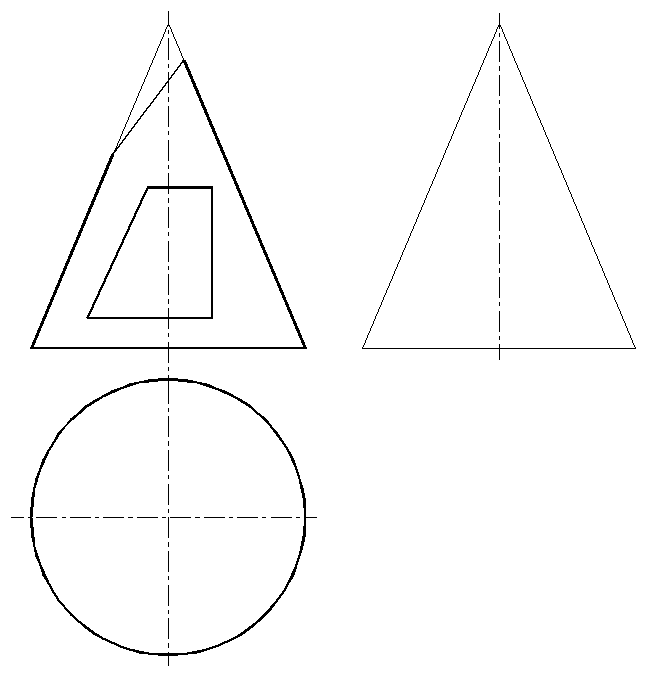
8. Построить горизонтальную и профильную проекции конуса, срезанного плоскостью и имеющего сквозное отверстие.

9. Построить недостающие проекции линии на поверхности наклонного конуса.

а) б)

10. Построить недостающие проекции точек, принадлежащих поверхности сферы.

11. Построить горизонтальную и профильную проекции сферы, усеченной плоскостями.

12. Построить горизонтальную проекцию линии ℓ на поверхности четверти сферы

13. Построить недостающие проекции линий, находящихся на поверхности четверти сферы.

14. Построить недостающие проекции поверхностей, усеченных фронтально проецирующими плоскостями.

а)

б)

15. Достроить горизонтальную проекцию тора, усеченного плоскостью ∑.

16. Построить недостающие проекции точек, принадлежащих поверхности тора.

17. Построить горизонтальную проекцию линии ℓ на поверхности тора.

18. Построить фронтальную проекцию линии ℓ на поверхности тора.

19. Построить горизонтальную и профильную проекции модели, усеченной плоскостью ∑, и натуральную величину фигуры сечения.

а)

б)

в)

д)

Раздел 3. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ.

1. Построить проекции точек А, В, С, изображенных на гранях и ребрах куба. Изобразить точки I, E, K на гранях и ребрах куба.

2. Построить изометрическую проекцию окружности диаметром 64 мм в плоскости, перпендикулярной оси Z. Точка О – центр окружности.

3. Построить изометрические проекции треугольников, расположенных в различных плоскостях проекции.

4. Построить изометрическую проекцию призмы с вырезом четверти, нанести штриховку.

6. Построить диметрическую проекцию модели с вырезом четверти, нанести штриховку.

5. Построить диметрические проекции четырехугольников, расположенных в различных плоскостях проекции.

7. Построить диметрические проекции окружности диаметром 100мм в плоскости, перпендикулярной оси Z, и в плоскости, перпендикулярной оси Y. Точки О₁ и О₂ – центры проекций.

8. Построить диметрию плоского четырехугольника ABCD, если его вершина С равноудалена от плоскости П₁ и П₂, а сторона ВС параллельна плоскости П₁.

Дата добавления: 2017-02-01