
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интегральные методы 1 страница
|
|
|
|
Интегральные методы основаны на использовании интегральных форм кинетических уравнений соответствующих порядков.
I. Метод подбора кинетического уравнения
а) Аналитический вариант метода. В кинетические уравнения, отвечающие первому, второму или третьему порядкам реакции, подставляют значения концентраций и соответствующее им время, прошедшее от начала реакции. Постоянство значений константы скорости считают весомым аргументом в пользу выбранного уравнения. Если же ни одно из уравнений не подходит, то это означает, что зависимость скорости реакции от концентрации не описывается степенным уравнением (5.6).
б) Графический вариант метода. Экспериментальные данные значений концентраций и соответствующее им время, прошедшее от начала реакции, представляют в координатах, дающих линейные зависимости:
для реакции первого порядка:  (рис. 5.2)
(рис. 5.2)
для реакции второго порядка:  (рис. 5.3)
(рис. 5.3)
для реакции нулевого порядка:  (рис. 5.4).
(рис. 5.4).
2. Метод определения времени, превращения на 1/ р часть исходного вещества (метод Оствальда–Нойеса)
Время превращения на 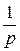 часть (
часть ( ) однозначно связано с начальной концентрацией исходного вещества (с 0) и порядком реакции (n):
) однозначно связано с начальной концентрацией исходного вещества (с 0) и порядком реакции (n):
n =1 
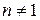
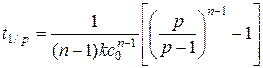 (5.31)
(5.31)
а) Аналитический вариант метода (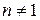 )
)
 ,
,
где  и
и  – время превращения на 1/р часть при начальных концентрациях исходного вещества с '0 и с 0, соответственно.
– время превращения на 1/р часть при начальных концентрациях исходного вещества с '0 и с 0, соответственно.
б) графический вариант метода. Логарифмируя выражение (5.31) получаем:

Проводят серию опытов с различными начальными концентрациями с 0 и находят время превращения исходного вещества на одну и ту же часть 1/р. Наклон прямой в координатах  дает значение n –1 (рис. 5.7).
дает значение n –1 (рис. 5.7).

Рис. 5.7. Логарифмическая зависимость времени превращения на 1/р часть от исходной концентрации
5.3. Зависимость скорости реакции от температуры
Скорость большинства химических реакций практически всегда увеличивается с повышением температуры. Температурная зависимость скорости реакции сводится к температурной зависимости константы скорости.
Согласно правилу Вант-Гоффа, для гомогенных реакций, протекающих при обычных температурах, с повышением температуры на 10 градусов скорость реакции увеличивается в 2 – 4 раза:
 (5.32)
(5.32)
Здесь γ – температурный коэффициент скорости реакции (отношение констант скоростей данной реакции при температурах Т+10 и Т).
Правило Вант-Гоффа носит весьма приближенный характер. Оно было установлено для реакций в растворах, протекающих при сравнительно низких температурах. При повышении температуры γ не остаётся постоянным.
Более точно зависимость константы скорости реакции от температуры описывается уравнением Аррениуса (1899 г.):
 (5.33)
(5.33)
или
 , (5.34)
, (5.34)
где k – константа скорости реакции, Т – абсолютная температура, R – универсальная газовая постоянная, А – предэкспоненциальный множитель, EА – энергия активации реакции.
В уравнении Аррениуса A и EА – кинетические параметры, не зависящие от температуры. Энергия активации EA – минимальная избыточная энергия молекул реагентов (по сравнению со средней), необходимая для их реакции при данной температуре. Эта энергия требуется для преодоления энергетического барьера реакции. Энергию активации обычно относят к одному молю вещества.
Экспоненциальный множитель 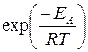 в уравнении Аррениуса можно рассматривать, как долю молекул, энергия которых превышает EA при температуре Т.
в уравнении Аррениуса можно рассматривать, как долю молекул, энергия которых превышает EA при температуре Т.
Уравнение Аррениуса выполняться и в случае сложных (многостадийных) процессов, когда константу скорости реакции можно выразить через константы скорости отдельных стадий. В таких случаях параметр EА в уравнении Аррениуса не имеет простого физического смысла и является некоторой функцией энергий активации указанных элементарных стадий. В случае сложных реакций параметр ЕА также принято называть энергией активации, хотя правильнее называть его эффективной или эмпирической (опытной) энергией активацией. Если константа скорости сложной реакции выражается через суммы или разности констант скоростей отдельных стадий, то температурная зависимость константы скорости носит более сложный характер, отличный от соотношения Аррениуса.
Дифференциальная форма уравнения Аррениуса:
 (5.35)
(5.35)
Интегрирование (неопределённое) уравнения (5.35) при условии, что ЕА не зависит от температуры, даёт
ln k =  + const, (5.36)
+ const, (5.36)
Сравнение (5.36) и (5.34) позволяет установить, что const = ln A.
В результате определённого интегрирования (5.35) получим:

и в принципе для определения ЕА достаточно знать константы скорости k 1 и k 2 при двух значениях температуры T 1 и T 2:
EA =  (5.37)
(5.37)
Однако такое определение ЕА не обеспечивает достаточной точности, и рекомендуется вычисления проводить не менее чем по четырем значениям констант скорости при соответствующих температурах.
В случае выполнения уравнения Аррениуса зависимость константы скорости от температуры в координатах  (аррениусовских) в соответствии с (5.34) должна графически изображаться прямой линией (рис. 5.8).
(аррениусовских) в соответствии с (5.34) должна графически изображаться прямой линией (рис. 5.8).

Рис. 5.8. Графическое определение энергии активации
Энергию активации определяют из тангенса угла наклона прямой a:
EА = – R ∙tg 
Предэкспоненциальный множитель А определяется отрезком, отсекаемым продолжением прямой на оси ординат при T –1= 0. Однако на практике А таким путём не определяют, поскольку экстраполяция к T –1=0 содержит слишком большую погрешность. Поэтому А вычисляют по известному значению ЕА и наборам значений k и Т, подставляя их в уравнение (5.33) или (5.34).
Для некоторых реакций опытные данные в координатах  не располагаются на прямой линии, что указывает на отклонение температурной зависимости константы скорости реакции от уравнения Аррениуса. Нелинейность графика объясняют зависимостью энергии активации от температуры для сложных реакций.
не располагаются на прямой линии, что указывает на отклонение температурной зависимости константы скорости реакции от уравнения Аррениуса. Нелинейность графика объясняют зависимостью энергии активации от температуры для сложных реакций.
5.4. Кинетика цепных реакций
Цепные реакции протекают с участием активных частиц (атомов, имеющих неспаренный электрон, свободных радикалов, ионов), причём химическое превращение осуществляется путём чередования элементарных актов взаимодействия с воспроизводством активных частиц. Образование активных частиц может происходить в результате распада исходных молекул под действием теплоты, света, электрического разряда и др.
Любая цепная реакция включает три стадии: зарождение цепи (инициирование), развитие (продолжение) цепи и обрыв цепи (гибель активных частиц). Зарождение цепной реакции, т.е. возникновение активных частиц, происходит при поглощении энергии исходным веществом. На стадии развития цепи активные частицы реагирует с исходным веществом, в результате чего образуются продукты реакции и новые активные частицы. Обрыв цепи обусловлен, как правило, взаимодействием активных частиц между собой, со стенками реакционного сосуда или с ингибитором (веществом, замедляющим процесс).
Если в элементарном акте одна активная частица воспроизводит одну новую активную частицу, то такую цепную реакцию называют неразветвлённой. В разветвлённых реакциях одна активная частица вызывает появление двух и более активных частиц, в результате чего их число по мере протекания реакции возрастает в геометрической прогрессии.
5.4.1. Неразветвлённые цепные реакции
Примером неразветвлённой цепной реакции является образование хлороводорода из водорода и хлора:
H2 + Cl2 = 2HCl
Механизм этой реакции можно представить следующим образом:
зарождение цепи: Cl2 → 2Cl •
продолжение цепи: Cl • + H2 → HCl + H •
H • + Cl2 → HCl + Cl •
Cl • + H2 → HCl + H •
обрыв цепи: Cl • + стенка → Cl(адс)
Cl • + Cl • + M → Cl2 + M,
где М – валентнонасыщенная молекула.
На стадии зарождения цепи (например в результате термической диссоциации молекулы хлора в газовой фазе) образуется атом хлора, который затем взаимодействует с молекулой водорода, давая хлороводород и атом водорода. В свою очередь, атом водорода вступает в реакцию с молекулой хлора и даёт молекулу хлороводорода и атом хлора. Таким образом, в каждом таком цикле помимо конечного продукта образуется свободный атом, дающий начало новому циклу превращений, т.е. происходит цепной процесс.
Образование активных частиц на стадии зарождения цепи может происходить в результате мономолекулярного распада исходного вещества при различных внешних воздействиях на систему, например, при действии света, тепла (в этом случае стадию зарождения цепи называют инициированием):
Cl2 
 2 Cl •;
2 Cl •;
C2H6  2CH3•
2CH3•
При бимолекулярном взаимодействии, например,
CH3CHO + O2 → CH3CO • + H2O,
активные частицы вследствие гетерогенной реакции исходного вещества, адсорбированного на внутренней поверхности (стенке) реакционного сосуда:
Cl2 + стенка → Cl2 + Cl(адс)
Продолжение цепи – стадии цепной реакции, идущие с сохранением свободной валентности и приводящие к расходованию исходных веществ и образованию продуктов реакции.
На стадии продолжения цепи возможны четыре типа реакций:
1) реакция свободного радикала (атома) R i • с молекулой одного из исходных веществ A, приводящая к образованию нового свободного радикала (атома) R2•;
2) реакция свободного радикала (атома) с молекулой одного из исходных веществ, приводящая к образованию нового свободного радикала (атома) и молекулы конечного продукта В:
R1• + A → R2• + B;
3) мономолекулярное превращение одного свободного радикала в другой (изомеризация):
R1• → R2•;
4) мономолекулярный распад свободного радикала с образованием молекулы продукта и нового свободного радикала (атома):
R1• → R2• + B.
В любой цепном процессе должна быть, по крайней мере, одна реакция, в которой расходуется исходное вещество (реакция типа 1 или 2), и одна, в которой образуются продукты (реакция типа 2 или 4).
На стадии обрыва цепи происходят реакции, приводящие к исчезновению активных частиц и, в итоге, к прекращению цепного процесса. Реакции обрыва цепей, скорость которых пропорциональна концентрации активных частиц, называют реакциями линейного обрыва цепей. Линейный обрыв цепи может быть обусловлен адсорбцией радикала на внутренней поверхности реакционного сосуда или взаимодействием радикалов с валентнонасыщенными молекулами.
Обрыв цепей на стенках реакционного сосуда играет важную роль в газовых цепных реакциях, особенно в цепных реакциях, идущих при низких давлениях.
Реакции обрыва цепей, скорость которых пропорциональна произведению концентраций двух свободных радикалов или квадрату концентрации какого-либо свободного радикала, называют реакциями квадратичного обрыва цепей. Квадратичный обрыв может происходить в результате рекомбинации двух радикалов, приводящей к образованию одной неактивной частицы, или вследствие диспропорционирования двух радикалов с образованием двух неактивных частиц. Квадратичный обрыв является основным путем гибели свободных радикалов в цепных реакциях, протекающих в жидкой и газовой фазе при больших давлениях, когда диффузия свободных радикалов к стенке и, следовательно, обрыв на стенке крайне затруднены.
Совокупность последовательных элементарных актов стадии продолжения цепи, из многократного повторения которых складывается цепной процесс, называют звеном цепи. Так, для процесса образования хлороводорода звеном цепи являются две элементарные реакции между свободным атомом хлора и молекулой водорода и между атомом водорода и молекулой хлора:
Cl • + H2 → HCl + H •
H • + Cl2 → HCl + Cl •
В звене цепи возрождается активная частица, которая была израсходована. Звено цепи чаще всего состоит из двух элементарных реакций, но их может быть и больше двух.
Среднее число полных звеньев цепи на стадии продолжения развития цепи называют длиной цепи. Длина цепи указывает на число молекул продукта реакции, приходящееся на одну первоначально активированную частицу. Длина цепи может составлять от десятков тысяч до десятков миллионов молекул. Длина цепи зависит от температуры, давления, наличия примесей, формы реакционного сосуда и состояния его стенок.
Существует некоторая вероятность  обрыва цепи на каждом её звене, при этом разность (1 –
обрыва цепи на каждом её звене, при этом разность (1 –  ) характеризует вероятность продолжения цепи. Длина цепи
) характеризует вероятность продолжения цепи. Длина цепи  равна отношению вероятностей продолжения и обрыва цепи на данном звене
равна отношению вероятностей продолжения и обрыва цепи на данном звене

С другой стороны, отношение вероятностей продолжения и обрыва цепи равно отношению скоростей стадий продолжения цепи v и обрыва цепи (гибели активных частиц) vг:
 =
= 
Отсюда следует, что скорость неразветвлённой цепной реакции определяется по скорости стадии продолжения цепи:
v = vг· 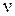
Для кинетического описания неразветвлённых цепных реакций можно применить метод стационарных концентраций. При условии стационарного режима реакции общее число активных частиц должно оставаться постоянным. Поскольку в цепной неразветвлённой реакции активные частицы появляются только на стадии зарождения цепи и исчезают на стадии обрыва цепи, скорость процесса зарождения v 0 равна сумме скоростей реакций обрыва цепи:
v 0 = 
Если обрыв происходит в результате одной реакции, то скорость зарождения равна скорости обрыва (v 0 = vг), тогда
v = v 0· 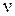 , (5.38)
, (5.38)
т.е. скорость неразветвленной цепной реакции равна произведению скорости стадии зарождения на длину цепи.
Из соотношения (5.38) вытекают характерные кинетические особенности неразветвленных цепных реакций, т.е. скорость такой реакции
– увеличивается с ростом скорости стадии зарождения цепи;
–зависит от состояния стенок реакционного сосуда, материала, из которого он изготовлен, размеров и формы;
– может быть уменьшена введением ингибиторов.
Последние два фактора влияют на длину цепи. Кинетическое уравнение для активных частиц неразветвленной цепной реакции в случае линейного обрыва цепи
 ,
,
где n – концентрация активных частиц, v 0 – скорость зарождения, g×n – скорость обрыва (гибели) цепи, g – константа скорости обрыва цепи.
Интегрирование этого уравнения приводит к следующему выражению


Через некоторое время после начала реакции концентрация активных частиц перестает изменяться (е– gt → 0):
 ,
,
т.е. устанавливается квазистационарный режим протекания процесса. При квазистационарном течении процесса  , т.е. число возникающих активных частиц равно числу гибнущих.
, т.е. число возникающих активных частиц равно числу гибнущих.
5.4.2. Разветвлённые цепные реакции
В каждом элементарном акте разветвлённой цепной реакции взаимодействует одна активная частица, а образуются две или более активных частиц. В результате элементарный акт даёт начало не одному, а двум или нескольким звеньям цепи – цепь разветвляется. Элементарная стадия цепной реакции, в которой превращение активных промежуточных частиц приводит к увеличению числа активных частиц, называется разветвлением цепи.
Примером разветвлённой цепной реакции является окисление водорода
H2 + ½ O2 → H2O
Предполагаемый механизм этой реакции при низких давлениях включает следующие стадии:
зарождение цепи
H2 + O2 → 2 OH • 
H2 + O2 → H • + HO2 •
HO2 • + H2 → OH • + H2O
продолжение и разветвление цепи
OH • + H2 → H2O + H •
H• + O2 → OH • + •O•
•O• + H2 → OH • + H •
обрыв цепи
H • + стенка → H(адс)
OH • + стенка → OH(адс)
H • + O2 + M → HO2 • + M
HO2 • + стенка → ½ H2O + ½ O2
Кинетика разветвлённых цепных реакций имеет ряд особенностей. В первый момент, когда происходит зарождение активных частиц, скорость реакции незначительна. Это - период индукции, в течение которого скорость реакции постепенно возрастает. Далее процесс быстро ускоряется и если он не доходит до взрыва, то скорость становится постоянной, а затем процесс начинает замедляться по мере уменьшения концентрации реагирующих веществ.
Кинетическое уравнение для активных частиц цепной разветвлённой реакции с линейным обрывом цепи записывают в виде:
 ,
, 
где n – концентрация свободных радикалов, v 0 – скорость зарождения цепей; f×n – скорость разветвления цепей; g×n – скорость стадии обрыва цепей; f и g – эффективные константы скорости соответственно разветвления и обрыва цепей.
Интегрирование этого уравнения приводит к кинетическим уравнениям, описывающим процесс накопления свободных радикалов в системе. При интегрировании необходимо учесть два возможных условия протекания разветвлённой цепной реакции.
1. Скорость разветвления больше скорости обрыва цепей, (f > g):

В этом случае имеет место прогрессирующее нарастание концентрации свободных радикалов, а следовательно, и скорости цепной реакции. При t → ∞ имеем n → ∞, т.е. число активных частиц увеличивается по экспоненциальному закону:

Практически полное отсутствие реакции сменяется взрывным протеканием процесса после периода индукции происходит воспламенение реакционной смеси. Воспламенение, вызванное резким ускорением реакции в результате прогрессирующего нарастания концентрации свободных радикалов при постоянной температуре, называют цепным воспламенением. Цепное воспламенение является общим свойством всех разветвленных цепных реакций.
2. Скорость разветвления меньше скорости обрыва цепи (f < g):
 (5.39)
(5.39)
Согласно уравнению (5.39) в системе через некоторое время устанавливается стационарная концентрация свободных радикалов  .
.
При рассмотренном условии протекание реакций разветвления приводит лишь к увеличению стационарного значения n по cравнению с неразветвлённой цепной реакцией, когда f = 0. Следовательно, в системе протекает цепная реакция, по кинетическим характеристикам принципиально не отличающаяся от неразветвлённых цепных реакций. На рис. 5.9 приведена зависимость n от времени.

Рис. 5.9. Зависимость концентрации активных частиц от времени при различных режимах протекания разветвленной цепной реакции
Переход от условия f < g к условию f > g может произойти при незначительном изменении одного из параметров, определяющих скорости обрыва или разветвления цепей: давления, температуры, состава реакционной смеси и наличия примесей, а также формы, размера, материала и состояния стенок сосуда. Незначительное изменение одного из этих параметров может привести к переходу от медленного стационарного процесса к быстрому взрывному и наоборот.
Резкое изменение скорости реакции при незначительном изменении условий её протекания получило название предельного (критического) явления. Возможность критических явлений – характерная черта разветвленных цепных реакций.
Для систем, в которых при определенных температуре, составе смеси, размере реакционного сосуда в определенном интервале давлений возможно цепное воспламенение, существуют два предела воспламенения – нижний и верхний. При достаточно малых давлениях скорость обрыва цепей, протекающих на стенках сосуда, больше скорости разветвления цепей. В этой области давлений взрыва не происходит даже при поджигании смеси. При увеличении давления система обнаруживает нижний предел взрываемости P н. В области от Р н до Р в (верхнего предела взрываемости) скорость разветвления цепей преобладает над скоростью обрыва (f > g) и реакция идёт со взрывом. При дальнейшем увеличении давления система обнаруживает верхний предел взрываемости (Р в) и при давлении выше этого предела реакция протекает без взрыва. Существование верхнего предела взрываемости связано с тем, что при повышении давления обрыв цепей в объёме, скорость которого пропорциональна квадрату давления, начинает преобладать над разветвлением цепей, скорость которой пропорциональна первой степени давления.
Пределы воспламенения зависят от температуры. Нижний предел воспламенения зависит от размеров реакционного сосуда. Чем больше диаметр сосуда, тем ниже скорость обрыва цепей на его стенках и ниже давление Р н, при котором наступает воспламенение. При малых размерах сосуда свободные радикалы легче достигают его поверхности и давление Р н выше. Эта закономерность используется на практике: на пути возможного распространения взрыва или воспламенения ставят трубки узкого диаметра или сетки, на которых обрываются цепи.
На рис. 5.10 приведена зависимость скорости реакции v от давления (или концентрации) для разветвленных цепей.

Рис.5.10.Зависимость скорости разветвленной цепной реакции от давления: Р н, Р в – нижний и верхний предел давлений соответственно.
Работа 5.1. Изучение кинетики разложения пероксида водорода газоволюметрическим методом
Пероксид водорода в водных растворах самопроизвольно медленно разлагается по уравнению
Н2О2 → Н2О + ½О2
Скорость реакции значительно увеличивается при повышении температуры или в присутствии катализаторов: ионов Fe2+, Fe3+, Сr2О72–, CrO42–, WO42–, МоО42–, смесей: CuSO4+МoО42–, CuSO4+NiSO4 и многих других. В определённых условиях реакция может протекать по первому или близкому к первому порядку. За ходом процесса удобно наблюдать по изменению объёма выделившегося кислорода через различные промежутки времени от начала реакции.
Цель работы. Определить порядок реакции каталитического разложения пероксида водорода.
Порядок выполнения работы. В настроенный на заданную температуру термостат помещают колбу вместимостью 200-300 см3 с 50 см3 раствора катализатора. Одновременно термостатируют реакционный сосуд 1 (рис. 5.11).
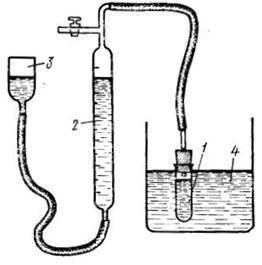
Рис. 5.11. Схема установки для изучения скорости разложения Н2О2 газометрическим методом:
1 – реакционный сосуд, 2 – бюретка, 3 – уравнительный сосуд, 4 – термостат.
Спустя 15-20 мин в колбу с раствором катализатора вливают определённое количество пероксида водорода (~0.7 см3), отметив этот момент как время начала реакции. Смесь тщательно размешивают и помещают реакционный сосуд, заполнив его так, чтобы высота воздушного пространства между уровнем жидкости и пробкой не превышала 2 см. Сосуд с реакционной смесью помещают в термостат 4 и соединяют с измерительной системой, состоящей из уравнительного сосуда 3 и бюретки 2, заполненных подкрашенной водой. Верхний кран в течение 1–2 мин держат открытым (связанным с атмосферой) для вытеснения воздуха выделяющимся кислородом из реакционного сосуда, затем выставляют положение жидкости в бюретке на ноль и кран закрывают, соединив таким образом реакционный сосуд с газовой бюреткой. После этого через 1 мин производят первое измерение и записывают уровень жидкости в бюретке и время.
Каждое следующее измерение сопровождается такой же записью, причем уровни жидкости в бюретке и уравнительном сосуде непрерывно поддерживаются одинаковыми. Измерения необходимо проводить через 1 мин до тех пор, пока выделяется больше, чем 1 см3 газа, затем увеличивать промежутки времени до 2, 3 и 5 мин. После того как реакция практически прекратится, реакционный сосуд помещают в кипящую водяную баню и выдерживают в ней до полного разложения пероксида водорода (около 15 - 20 мин). При кипячении на водяной бане уравнительный сосуд должен находиться в наиболее низком положении. Затем реакционный сосуд снова помещают в термостат на 15–20 мин и измеряют уровень жидкости в бюретке. Результаты записывают в табл. 5.1.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 114; Нарушение авторских прав?; Мы поможем в написании вашей работы!