
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод сферического посредника
|
|
|
|
Тема 10. Взаимное пересечение поверхностей.
Вопросы:
1. По каким линиям пересекаются две соосные поверхности вращения?
2. При каких условиях сфера пересекается с поверхностью вращения по окружностям?
3. При каких условиях сфера пересекается с циклической поверхностью по окружности?
4. Как определяются наибольший и наименьший радиусы концентрических сфер посредников?
Исходные данные к заданию “Пересечение поверхностей”
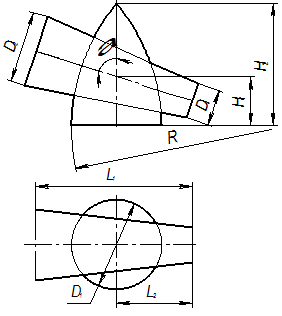
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таблица 6
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
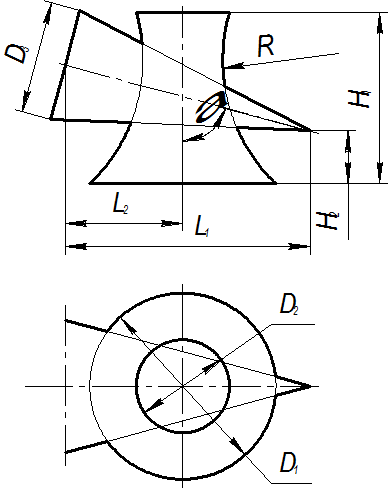
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таблица 7
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таблица 8
|
Пример 8. Заданы коническая и цилиндрическая поверхности вращения, имеющие общую плоскость симметрии, параллельную фронтальной плоскости проекций. Построить линию их пересечения (рис. 7).
Последовательность решения задачи:
1) исходные данные удовлетворяют условиям применимости метода концентрических сфер для построения линии пересечения двух поверхностей, который и используем для решения задачи;
2) определяем центр сфер посредников – точку О (находится в пересечении осей поверхностей);
3) определяем сферы минимального Rmin и максимального Rmax радиусов; сфера Rmin касается конической поверхности и пересекает цилиндрическую; сфера Rmax проходит через наиболее удаленную от точки О точку пересечения очерков поверхностей;
4) для каждой сферы строим окружности, по которым она пересекает заданные поверхности; пересечение соответствующих окружностей задаёт пары точек искомой линии пересечения.
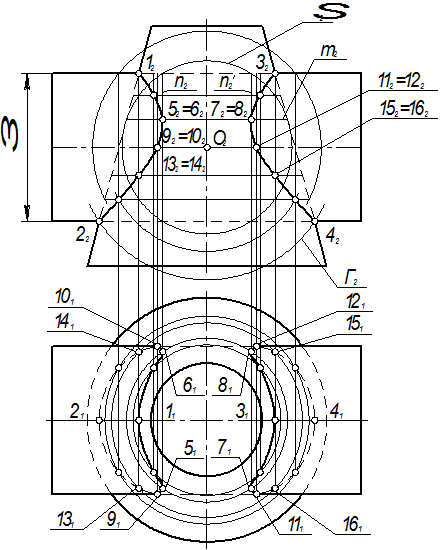
Рис. 7
Список литературы:
1. Четверухин Н.Ф., Левицкий В.С. Начертательная геометрия. – М.: Высш. шк., 1972 – 310 с.
2. Арустамов Х.А. Сборник задач по начертательной геометрии. – М.: Машиностроение, 1971 – 375 с.
3. Бубенников А.В., Громов М.Я. Начертательная геометрия. – М.: Высш. шк., 1973 – 210 с.
4. Кошелева Л.И., Леонова Л.М., Ляшков А.А. Задания по инженерной графике. Методические указания. Омск, 2001 – 54 с.
5. ГОСТ 2.301-68. Форматы. – М.: ГОССТАНДАРТ, 1991. – 236 с.
6. ГОСТ 2.303-68. Линии. – М.: ГОССТАНДАРТ, 1991. – 236 с.
7. Ляшков А.А. Начертательная геометрия: Конспект лекций / А.А. Ляшков, Л.К. Куликов, К.Л. Панчук. – Омск: Изд-во ОмГТУ, 2005. – 108 с.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 86; Нарушение авторских прав?; Мы поможем в написании вашей работы!