Узагальнюючі показники рядів розподілу.

Середньою величиною у статистиці називається узагальнююча характеристика сукупності однотипних явищ з будь-якої варіаційної ознаки, що показує рівень ознаки, розрахований на одиницю сукуп­ності. Разом із методом групувань середні величини у статистиці є одним з основних методів опрацювання й аналізу масових даних.

Середня величина як категорія стати­стики — це, з одного боку, реальний показник, що відображає об'єк­тивно існуючі властивості суспільних явищ, на основі яких можуть бути обчислені середні показ­ники; а з другого — у ній взаємознищуються індивідуальні розхо­дження багатьох величин одного і того самого виду.

У статистиці застосовуються кілька видів середніх величин. Усі вони належать до класу степеневих середніх, загальна формула якої має такий вигляд: ,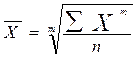

де 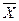- середня величина; X — варіанта; т — показник степеня середнь­ої; n - число одиниць сукупності.

Якщо т = 1, то середня арифметична - ;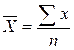

Якщо т = 2, то середня квадратична - ;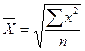

Якщо т = -1, то середня гармонійна - ;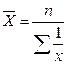

Якщо m=0, то середня геометрична - ,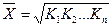

де К₁, К₂, ….К_n – ланцюгові коефіцієнти динаміки.

Крім степеневих середніх величин, у статистиці застосо­вуються описові характеристики ряду розподілу ознаки — мода (Мо) і медіана (Ме).

Середню арифметичну визначають як відношення суми окремих значень ознаки до кількості одиниць сукупності. Розрізняють середню арифметичну просту та зважену. Середню арифметичну просту застосовують тоді, коли відомі індивідуальні значення усередненої ознаки у кожній одиниці сукупності. Середня арифметична зважена обчислюється, коли окремі значення усередненої ознаки повторюються у досліджуваній сукупності неоднакове число разів, а зважування в цьому випадку проводять за частотами, які показують скільки разів повторюється певний варіант. Середня геометрична величина використовується для визначення середніх темпів динаміки значимих явищ. Середня квадратична величина застосовується при вивченні зв'язків між досліджуваними явищами та їх причинами методом ко­реляційного аналізу та ін.

Застосуємо теоретичний матеріал до нашого проектного завдання і розрахуємо прості середні величини.

Таблиця 8

Вихідні та розрахункові дані для обчислення простих середніх величин

№ п/п	Y	Х1	Х2	1/Y	Y^2	1/ X1	X1^2	1/ X2	X2^2
		0,63	5,71	0,143		1,587	0,397	0,175	32,604
	5,5	0,59	3,54	0,182	30,25	1,695	0,348	0,282	12,532
	10,6	0,64	6,54	0,09	112,36	1,563	0,41	0,153	42,772
	3,7	0,56	4,51	0,27	13,69	1,786	0,314	0,222	20,34
	13,4	1,46	3,73	0,07	179,56	0,685	2,132	0,268	13,913
	3,7	0,64	3,94	0,27	13,69	1,563	0,41	0,254	15,524
	5,9	0,72	6,53	0,169	34,81	1,389	0,518	0,153	42,641
	7,5	0,85	6,9	0,133	56,25	1,176	0,723	0,145	47,61
	8,7	0,65	3,28	0,115	75,69	1,538	0,423	0,305	10,758
	5,1	0,63	7,85	0,196	26,01	1,587	0,397	0,127	61,623
	5,7	0,5	4,74	0,175	32,49		0,25	0,211	22,468
	11,8	0,77	3,24	0,08	139,24	1,299	0,593	0,309	10,498
	5,9	0,56	6,67	0,169	34,81	1,786	0,314	0,15	44,489
	9,8	0,54	2,36	0,102	96,04	1,852	0,292	0,424	5,57
	6,7	0,5	3,33	0,149	44,89		0,25	0,3	11,089
	10,6	1,23	3,97	0,09	112,36	0,813	1,513	0,252	15,761
	5,2	0,65	5,52	0,192	27,04	1,538	0,423	0,181	30,47
	4,3	0,5	2,14	0,233	18,49		0,25	0,467	4,58
	7,6	0,6	5,4	0,132	57,76	1,667	0,36	0,185	29,16
	6,3	0,78	2,17	0,159	39,69	1,282	0,608	0,461	4,709
	3,9	0,6	1,43	0,256	15,21	1,667	0,36	0,699	2,045
	12,1	0,88	10,36	0,08	146,41	1,136	0,774	0,097	107,33
	13,3	1,38	3,8	0,075	176,89	0,725	1,904	0,263	14,44
	12,5	0,95	3,94	0,08	156,25	1,053	0,903	0,254	15,524
	7,8	0,71	5,65	0,128	60,84	1,408	0,504	0,177	31,923
Разом	194,6	18,52	117,25	3,738	1714,72	36,795	15,37	6,514	650,373

Розрахуємо середню арифметичну просту для результативної та двох факторних ознак:

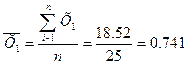
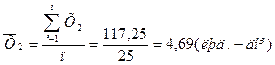
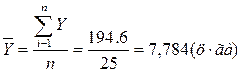
Розрахуємо середню гармонійну просту для результативної та двох факторних ознак:

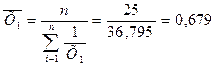
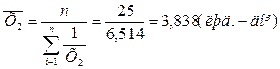
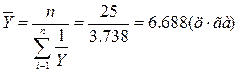
Розрахуємо середню квадратичну просту для результативної та двох факторних ознак:

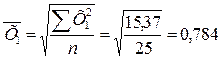
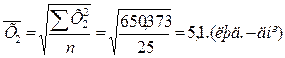
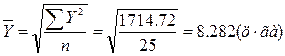
Перевірити правильність розрахунку середніх величин ми можемо використавши правило мажорантності. Суть його полягає в тому що середня гармонійна завжди менша ніж середня арифметична, а та в свою чергу ще менша ніж середня квадратична. Тобто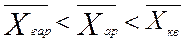

Для урожайності: 6,688<7.784<8.282

Для якості: 0,679<0.741<0.784

Для прямих затрат: 3,838<4.69<5.1

Як бачимо, правило мажорантності виконується.

Розрахуємо середні арифметичні зважені та підтвердимо розрахунок способом моментів.

Середня способом моментів обчислюється за формулою:

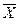=m₁i + a,

де m₁ – момент першого порядку. Він дорівнює: ,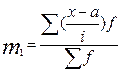

де а – число, на яке зменшуються усі варіанти, частіше це варіанта, що перебуває в середині ряду або має найбільшу частоту; і – величина інтервалу.

Таблиця 9

Розрахунок середньої арифметичної способом моментів

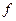
№ п/п	Групи за якістю льонотрески	Частоти	Центр інтервалу,		,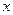
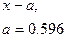
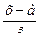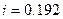
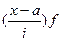
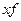
	0,5-0,692		0,596				8,94
	0,692-0,884		0,788	0,192			4,728
	0,884-1,076		1,96	1,364	7,104	7,104	1,96
	1,076-1,268		1,172	0,576			1,172
	1,268-1,46		1,364	0,788			2,728
	Разом		Х	Х	Х	24,104	19,528

Результати обчислень, наведених у таблиці, підставляємо у формулу:

=

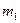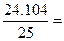
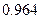
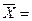
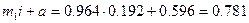
Паралельно визначаємо середню арифметичну зважену:

.

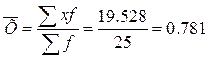Отже, середня арифметична, розрахована двома різними способами, дає один і той самий результат, і ми можемо стверджувати, що середній рівень якості по сукупності становить 0,781.

Дата добавления: 2017-02-01