Характеристики направленности антенны

Точечный изотропный излучатель является абсолютно ненаправленным. Но это абстракция: любая реальная антенна хотя бы немного направленная.

Характеристикой направленности антенны называется зависимость комплексной амплитуды напряженности поля изучения от угловых координат точки наблюдения при условии измерения этого поля на одинаковом расстоянии r от антенны. Комплексная амплитуда имеет модуль E_m и аргумент ; кроме того, волна характеризуется поляризацией. Соответственно характеристики направленности разделяются на амплитудные, фазовые и поляризационные. Чаще всего используются амплитудные (в таких случаях слово«комплексная» опускается).

Функция, описывающая характеристику направленности, называется функцией направленности, а ее графическое изображение - диаграммой направленности (ДН).

Исследуя направленные свойства антенны, полагают, что антенна
находится в центре О сферы, а точка наблюдения М расположена на
поверхности этой сферы(рисунок 7.4). Сферические координаты точек наблюдения: дальность (радиус сферы) r, азимут φ, зенитный угол θ или
угол места δ= 90⁰ —θ.

Рисунок 7.4 – Сферические координаты точки наблюдения

Кроме деления на амплитудные, фазовые и поляризационные, ДН классифицируют по следующим признакам.

1. По полю и мощности. ДН по полю выражает зависимость амплитудного Е_т или действующего Е значения напряженности поля от направления (углов , θ), а ДН по мощности – от плотности потока мощности П. Так как плотность потока мощности пропорциональна квадрату напряженности поля (), то если ДН по полю выражается функцией , то ДН по мощности функцией .

Например, амплитуда напряженности электрического поля диполя Герца в направлении зенитного угла θ

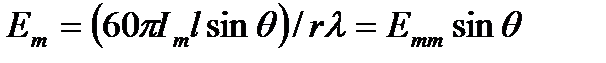, (7.7)

где максимальная амплитуда поля, соответствующая θ=90,270⁰. Из (7.7) находим функции направленности диполя Герца по полю и мощности

f (θ) = sinθ, (7.8)

f ²(θ) = sin²θ. (7.9)

2. Пространственные (объемные) и плоскостные ДН. Пространственная ДН – функция двух углов , θ и представляет собой поверхность , которая охватывает определенный объем (рисунок 7.5).

Рисунок 7.5 – Пространственная (объемная) ДН диполя Герца

Плоскостная ДН является функцией одного угла и представляет собой плоскую фигуру (рисунок 7.6).

Обычно для построения ДН выбирают плоскости, проходящие через направления максимального излучения – главные плоскости. Одна из них совпадает с вектором Е и называется Е - плоскостью, а другая – с вектором Н и называется Н - плоскостью.

3. По выбранной для построения ДН системе координат – полярной или прямоугольной. В полярной системе координат на радиусе, расположенном под углом θ или к исходному направлению, откладывают отрезок, длина которого пропорциональна абсолютному значению (рисунок 7.6, а) или (рисунок 7.6, б), а затем концы отрезков, отложенных для различных углов θ или , соединяют. В прямоугольной системе координат углы θ или откладывают по оси абсцисс, а (рисунок 7.6, в) или (рисунок 7.6, д) - по оси ординат и полученные точки также соединяют.

Рисунок 7.6 – Амплитудные (а, б, в, д) и фазовая (г) ДН диполя Герца,

построенные в полярных (а, б) и прямоугольных (в-д) координатах

Функции направленности диполя Герца соответствует пространственная ДН в виде тора – тела вращения окружности диаметром вокруг оси диполя (рисунок 7.5). Сечения тора главными плоскостями – амплитудные ДН по полю, причем ДН в Е-плоскости f(θ)=sinθ имеет в полярных координатах форму восьмерки (рисунок 7.6, а), а в прямоугольных – полусинусоид положительного знака (рисунок 7.6, в); ДН в Н-плоскости имеет форму окружности в полярных (рисунок 7.6, б) и прямой, параллельной оси абсцисс, в прямоугольных координатах (рисунок 7.6, д). Отсутствие направленности в Н -плоскости (f()=const) согласуется с тем, что в выражение для функции направленности угол не входит.

Фазовая ДН (рисунок 7.6, г) отражает скачкообразное изменение фазы
поля ψ на 180⁰: когда зенитный угол проходит значения θ=180,360⁰
функция f(θ)=sinθ изменяет знак.

ДН по мощности , показанная штриховой линией
на рисунке 7.6, а, в, совпадает с ДН по полю в точках, где θ=0, 90, 180, 270, 360⁰, а при остальных значениях θ функция .

Из расположения векторов Е, Н и П на рисунке 7.6, а, б видно, что
Е-плоскость меридианальная (вертикальная), а Н-плоскость – экваториальная (горизонтальная). Это характерно для антенн с осевой симметрией. Плоскостные ДН как более простые применяются чаще, чем пространственные.

4. По выбранным масштабам отсчета ДН. ДН многих антенн, особенно остронаправленных, имеют многолепестковую структуру (рисунок 7.7): кроме главного лепестка (луча) (1), они содержат боковые (2, 3) и задний (4) лепестки. В таких случаях предпочтительнее изображение ДН в прямоугольных координатах (рисунок 7.7, б), на котором можно выбрать любой масштаб по осям и этим представить слабые боковые и задний лепестки более отчетливо, чем на полярной ДН (рисунок 7.7, а).

Рисунок 7.7 – Нормированные ДН по мощности в линейном (а, б) и

логарифмическом (в) масштабах

Различают ненормированные и нормированные ДН. Нормирование
означает, что величины Е_т и П в направлении отнесены к их максимальным значениям Е_тт и П_m. Функции нормированных ДН по полю н мощности обозначаются через

, (7.10)

. (7.11)

Нормированные ДН удобно представлять в логарифмическом масштабе, при котором функции направленности выражаются в децибелах. Децибел – это десятая доля бела, который определяется десятичным логарифмом отношения мощностей, т. е.

, (7.12)

По данной формуле составлена таблица 7.1, иллюстрирующая пересчет
в децибелы N [дБ] нормированной функции направленности но мощности и по полю .

Таблица 7.1

		1,26	1,58
		1,12	1,26	1,41		3,16		31,6
N,дБ

Например, по ДН, показанной на рисунке 7.7, в уровень первого бокового лепестка (2) ниже уровня луча (1) на 6 дБ, т. е. меньше в два раза по напряженности поля и в четыре раза по мощности.

Заметим еще, что если функция имеет максимум , то ненормированная и нормированная ДН совпадают: , как, например, для диполя Герца (рисунок 7.6).

Дата добавления: 2017-02-01